感動！この問題の答えが美しすぎる！超気持ちいい良問！【集合体恐怖症の方は閲覧注意】【中学受験算数】【入試問題】【帝京大学中】 - 質問解決D.B.（データベース）
Generic selectors
完全一致検索
タイトルから検索
記事本文から検索
Post Type Selectors
all_unit_post
質問解決D.B.（データベース） > 動画投稿 > 算数(中学受験) > 平面図形 > 角度と面積 > 感動！この問題の答えが美しすぎる！超気持ちいい良問！【集合体恐怖症の方は閲覧注意】【中学受験算数】【入試問題】【帝京大学中】

感動！この問題の答えが美しすぎる！超気持ちいい良問！【集合体恐怖症の方は閲覧注意】【中学受験算数】【入試問題】【帝京大学中】

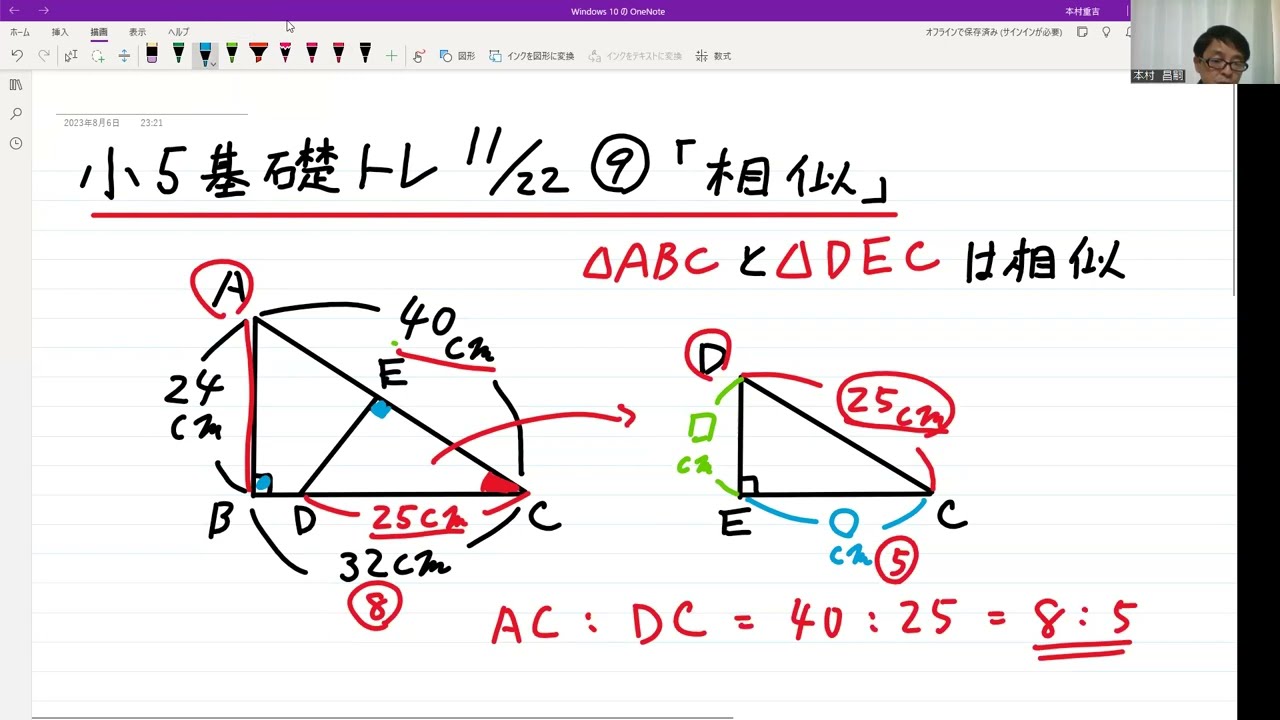
問題文全文(内容文)：
2021日本大学中学校
直角三角形ABCを、Cを中心として90°回転させたとき、太線内の面積は？

2021成蹊中学校
1辺が12cmの正方形ABCDの中に、点B、点Cのそれぞれを中心とする半径12cmの
円の一部をかき、さらに対角線ACをかく。
このとき,
(1)㋐の部分の周の長さは?

(2)㋐と㋑の部分の面積差は?

2021帝京大学中学校
左図は正方形と円を組み合わせた図形です。斜線部分の面積は？
（円周率は3.14）

＊図は動画内参照
チャプター：

0:00​　オープニング
0:17　今日の内容説明
1:16　１問目　ウォーミングアップ問題　問題提示
1:47　１問目　ウォーミングアップ問題　問題解説
5:38　２問目　問題提示
6:08　２問目　１題目　㋐の週の長さ　問題解説
11:21　２問目　２題目　㋐と㋑の面積差　問題解説
16:11　３問目　サムネイルの問題　問題提示
16:58　３問目　サムネイルの問題　問題解説
22:09　まとめ
22:28　家庭教師のアスピレーション　生徒募集のご案内
23:33　おすすめ動画紹介（ピアノ演奏付き）

単元： #算数(中学受験)#平面図形#角度と面積
指導講師： こばちゃん塾
問題文全文(内容文)：
2021日本大学中学校
直角三角形ABCを、Cを中心として90°回転させたとき、太線内の面積は？

2021成蹊中学校
1辺が12cmの正方形ABCDの中に、点B、点Cのそれぞれを中心とする半径12cmの
円の一部をかき、さらに対角線ACをかく。
このとき,
(1)㋐の部分の周の長さは?

(2)㋐と㋑の部分の面積差は?

2021帝京大学中学校
左図は正方形と円を組み合わせた図形です。斜線部分の面積は？
（円周率は3.14）

＊図は動画内参照
投稿日：2022.03.14

＜関連動画＞

【中学受験算数】100%解ける方法を伝授！単位分数の和で表す方法！開成中の難問にも対応可能！【毎日少しずつ中学受験算数７３】

アイキャッチ画像
単元： #算数(中学受験)#計算と数の性質#いろいろな計算#過去問解説(学校別)#開成中学
指導講師： こばちゃん塾
問題文全文(内容文)：
1⃣$\frac{11}{16} = \frac{1}{▢} + \frac{1}{△} + \frac{1}{○}$

2⃣$\frac{1}{4} = \frac{1}{▢} + \frac{1}{△} $

3⃣2010年開成中学校
$\frac{1}{12} = \frac{1}{△} + \frac{1}{▢} $（▢は△以上）
この動画を見る　

他に解き方があるよ！っという方は是非コメント欄に！！

アイキャッチ画像
単元： #算数(中学受験)#平面図形#角度と面積
指導講師： 数学を数楽に
問題文全文(内容文)：
正方形の1辺の長さを求めよ
＊図は動画内参照
この動画を見る　

桐島聡は逃走中なら何円稼いだ？

アイキャッチ画像
単元： #算数(中学受験)#計算と数の性質#いろいろな計算
指導講師： 【楽しい授業動画】あきとんとん
問題文全文(内容文)：
・逃走歴49年＝49×365.25×24×60×60
(フジテレビ　逃走中では40分に逃げ切れると120万）
・1秒で500円

桐島聡容疑者が逃走中をやっていたとしたら、
7731億6120万円稼げた事になる。
この動画を見る　

【小３　算数】　　小３－７　　わり算②　・　文章題

アイキャッチ画像
単元： #算数(中学受験)#計算と数の性質#いろいろな計算#約数・倍数を利用する問題#文章題#単位・比と割合・比例・反比例
指導講師： とある男が授業をしてみた
問題文全文(内容文)：
式を求めよう。
①30このあめを5人で分けます。 1人分は何こになるかな?
式:
② 56cmのリボンがあります。 8cmずつ切ると何本になるかな?
式:
③ 1箱に12こ入っているチョコが3箱 あります。全部で何このチョコがあるかな?
式:
④ マンガを、まもるくんは24冊、妹は4冊もって います。まもるくんの数は、妹の何倍かな?
式:
⑤$520dL$のジュースがあります。$4dL$のんだら、のこりは何$dL$かな?
式:
⑥ 赤いリボンは、青いリボンの 何倍かな?
式:
この動画を見る　

【小6算数手元解説】受験算数　正方形は何個？長方形は何個？【問題文は概要欄】

アイキャッチ画像
単元： #算数(中学受験)#場合の数#場合の数
教材： #SPX#中学受験教材#6年算数D-支援
指導講師： 理数個別チャンネル
問題文全文(内容文)：
下の図は一辺1cmの正方形を並べたものです。次の問いに答えなさい。(1) この図のなかにはいろいろな大きさの正方形があります。正方形は全部で何個ありますか。 (2) この図のなかにはいろいろな大きさの長方形があります。長方形(ただし、正方形は除く)は全部で何個ありますか。
この動画を見る　
PAGE TOP