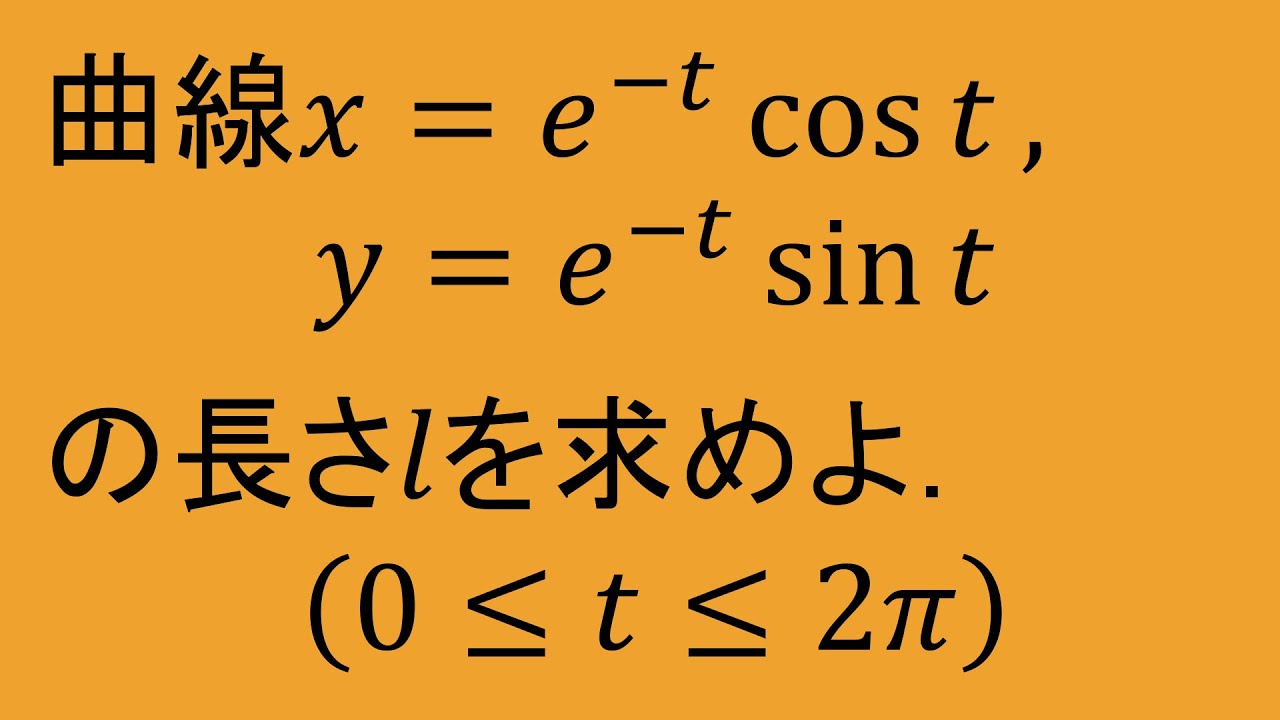問題文全文(内容文):
$x$と$y$の関係が次の式で与えられるとき、
$\dfrac{dy}{dx}$を$t$で表せ。
①$x=\dfrac{1}{1+t^2},y=\dfrac{t}{1+t^2}$
②$x=a(t-\sin t),y=(1-\cos t)\quad (a\gt 0)$
$x$と$y$の関係が次の式で与えられるとき、
$\dfrac{dy}{dx}$を$t$で表せ。
①$x=\dfrac{1}{1+t^2},y=\dfrac{t}{1+t^2}$
②$x=a(t-\sin t),y=(1-\cos t)\quad (a\gt 0)$
単元:
#平面上の曲線#微分とその応用#色々な関数の導関数#媒介変数表示と極座標#数学(高校生)#数C#数Ⅲ
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
$x$と$y$の関係が次の式で与えられるとき、
$\dfrac{dy}{dx}$を$t$で表せ。
①$x=\dfrac{1}{1+t^2},y=\dfrac{t}{1+t^2}$
②$x=a(t-\sin t),y=(1-\cos t)\quad (a\gt 0)$
$x$と$y$の関係が次の式で与えられるとき、
$\dfrac{dy}{dx}$を$t$で表せ。
①$x=\dfrac{1}{1+t^2},y=\dfrac{t}{1+t^2}$
②$x=a(t-\sin t),y=(1-\cos t)\quad (a\gt 0)$
投稿日:2018.05.26