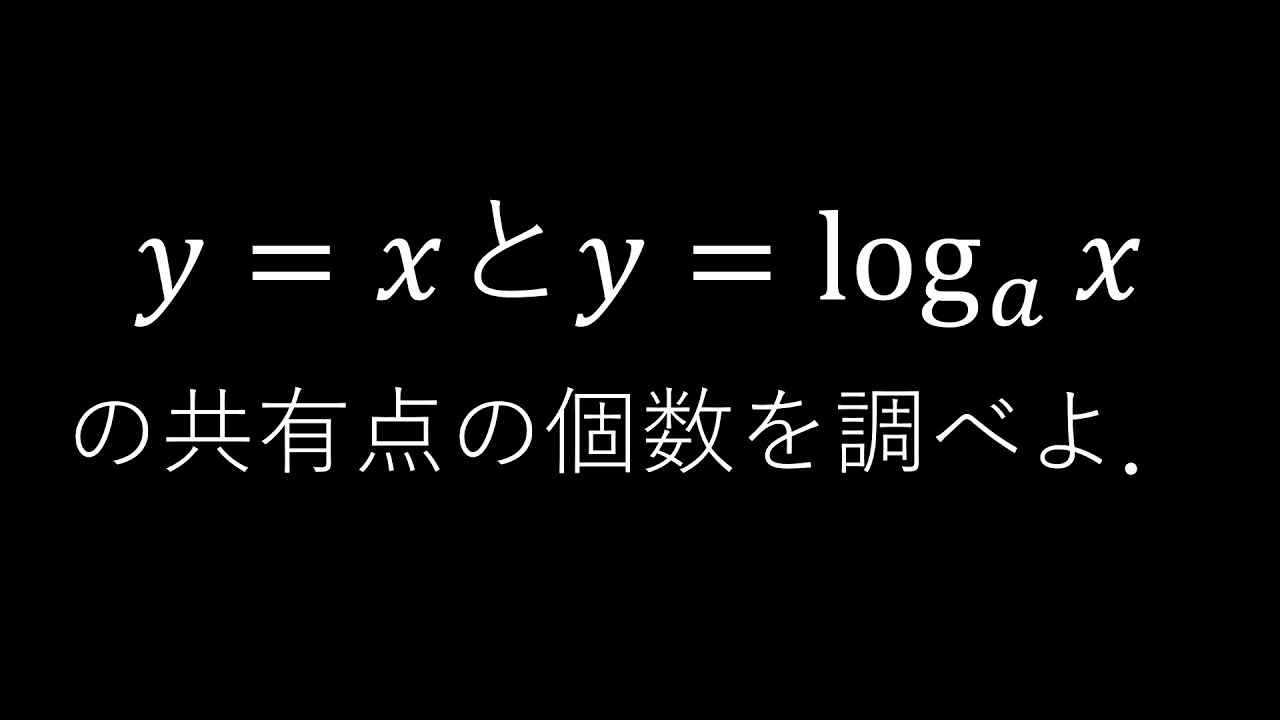19東京都採用試験（数学：対数）

問題文全文(内容文)：
2⃣-(2)
$2^x=3^y=18^z={}^3\sqrt6$
(1)$\frac{1}{x} + \frac{1}{y}$
(2)$\frac{1}{x} - \frac{1}{y}+\frac{2}{z}$

単元： #数Ⅱ#指数関数と対数関数#対数関数#数学(高校生)

指導講師：ますただ

問題文全文(内容文)：
2⃣-(2)
$2^x=3^y=18^z={}^3\sqrt6$
(1)$\frac{1}{x} + \frac{1}{y}$
(2)$\frac{1}{x} - \frac{1}{y}+\frac{2}{z}$

投稿日：2020.06.26

＜関連動画＞

【数Ⅱ】対数関数：ええ！？マイナスがついていないのにマイナスになる数が存在するのかい！？

単元： #数Ⅱ#指数関数と対数関数#対数関数#数学(高校生)

指導講師：理数個別チャンネル

問題文全文(内容文)：
マイナスがついていないのにマイナスの値になる数があります。
一体その正体とは…？？？？

補足：底が省略されている場合は基底e(約2.7)が省略されています(数Ⅲで習いますが今回の説明にはあまり影響はありません)

この動画を見る　

福岡大（医）連立指数方程式

単元： #数Ⅱ#大学入試過去問(数学)#指数関数と対数関数#指数関数#対数関数#学校別大学入試過去問解説(数学)#数学(高校生)#福岡大学

指導講師：鈴木貫太郎

問題文全文(内容文)：
$x,y$は1でない正の実数であるとする.これを解け.

$\begin{eqnarray}
\left\{
\begin{array}{l}
x^{x+y}=y^{10} \\
y^{x+y}=x^{90}
\end{array}
\right.
\end{eqnarray}$

福岡大(医)過去問

この動画を見る　

福田の数学〜立教大学2025理学部第1問(1)〜不等式と対数

単元： #数Ⅱ#大学入試過去問(数学)#指数関数と対数関数#対数関数#学校別大学入試過去問解説(数学)#立教大学#数学(高校生)

指導講師：福田次郎

問題文全文(内容文)：

$\boxed{1}$

(1)自然数$n$に対して$a_n=2^n$とし、

積$a_1a_2\cdots a_n$を$A_n$とおく。

このとき、$A_n \geqq 10^{10}$を満たす最小の

$n$は$\boxed{ア}$である。

ただし、$\log_2 10=3.3219$とする。

$2025$年立教大学理学部過去問題

この動画を見る　

福田の数学〜立教大学2024年経済学部第1問(1)〜対数関数の最小値

単元： #数Ⅱ#大学入試過去問(数学)#指数関数と対数関数#対数関数#学校別大学入試過去問解説(数学)#立教大学#数学(高校生)

指導講師：福田次郎

問題文全文(内容文)：
$1\leqq x\leqq 8$の範囲において、関数$y=(\log_{2} x)^2-8\log_{2} x-20$は$x=\fbox{ア}$のときに最小値$\fbox{イ}$をとる。

この動画を見る　

早稲田大（国際教養）対数とガウス記号

単元： #数Ⅱ#指数関数と対数関数#対数関数#数学(高校生)

指導講師：鈴木貫太郎

問題文全文(内容文)：
$x\gt 0$とする.
$m=\left[\log_{10}\dfrac{3\sqrt x}{20}\right]$
$n=\left[\log_{10}\dfrac{800}{x}\right]$
$3m+n$のとりうる値を求めよ.

早稲田(国際教)過去問

この動画を見る　

<img src="https://kaiketsu-db.net/wp-content/uploads/2021/11/112-book-morph-outline.gif" alt="" data-eio="l"> 19東京都採用試験（数学：対数）

＜関連動画＞

【数Ⅱ】対数関数：ええ！？マイナスがついていないのにマイナスになる数が存在するのかい！？

福岡大（医）連立指数方程式

福田の数学〜立教大学2025理学部第1問(1)〜不等式と対数

福田の数学〜立教大学2024年経済学部第1問(1)〜対数関数の最小値

早稲田大（国際教養）対数とガウス記号

19東京都採用試験（数学：対数）