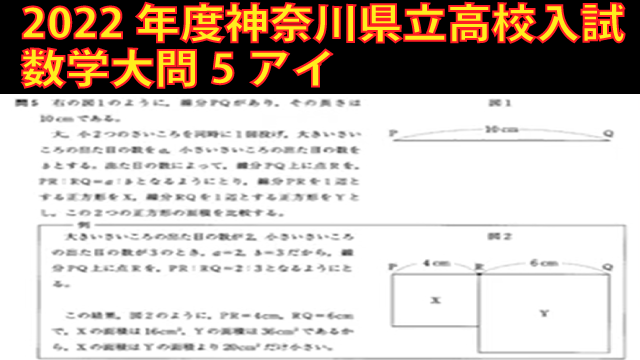
問題文全文(内容文):
(ア) 右の図1のように,AB<AC,∠ABCが鋭角の平行四辺形ABCDがあり,∠BCDの二等分線と辺ADとの交点をEとする。
また,辺BCの延長上に点Fを,CF=DFとなるようにとる。
さらに,辺CD上に点Gを,CG>GDとなるようにとり,線分DF上に点Hを,DG=DHとなるようにとる。
このとき,三角形DEGと三角形DCHが合同であることを証明しなさい。
(ア) 右の図1のように,AB<AC,∠ABCが鋭角の平行四辺形ABCDがあり,∠BCDの二等分線と辺ADとの交点をEとする。
また,辺BCの延長上に点Fを,CF=DFとなるようにとる。
さらに,辺CD上に点Gを,CG>GDとなるようにとり,線分DF上に点Hを,DG=DHとなるようにとる。
このとき,三角形DEGと三角形DCHが合同であることを証明しなさい。
チャプター:
00:00 オープニング
00:09 証明問題の説明
00:33 (a)の解答
02:25 (b)(c)の解答
単元:
#数学(中学生)#高校入試過去問(数学)#神奈川県公立高校入試
指導講師:
理数個別チャンネル
問題文全文(内容文):
(ア) 右の図1のように,AB<AC,∠ABCが鋭角の平行四辺形ABCDがあり,∠BCDの二等分線と辺ADとの交点をEとする。
また,辺BCの延長上に点Fを,CF=DFとなるようにとる。
さらに,辺CD上に点Gを,CG>GDとなるようにとり,線分DF上に点Hを,DG=DHとなるようにとる。
このとき,三角形DEGと三角形DCHが合同であることを証明しなさい。
(ア) 右の図1のように,AB<AC,∠ABCが鋭角の平行四辺形ABCDがあり,∠BCDの二等分線と辺ADとの交点をEとする。
また,辺BCの延長上に点Fを,CF=DFとなるようにとる。
さらに,辺CD上に点Gを,CG>GDとなるようにとり,線分DF上に点Hを,DG=DHとなるようにとる。
このとき,三角形DEGと三角形DCHが合同であることを証明しなさい。
投稿日:2022.11.17