問題文全文(内容文)：
1⃣
$\triangle ABC$において、$b=2,c=3,A=60^{ \circ }$のとき、$a$を求めよ。

2⃣
$\triangle ABC$において、$a=8,b=5,c=7$のとき、$C$を求めよ。

問題文全文(内容文)：
1. x+y+z=10の正の整数解の個数を求めよ。

2. 3つのサイコロを投げる。
出る目の最大値と最小値の差が2になる確率を求めよ。

3. 複素数$(\frac{-1+\sqrt{3}i}{2})^{2015} + (\frac{-1-\sqrt{3}i}{2})^{2015}$

4. $log_{2}3$は無理数を示せ

5. $△OAB = \frac{|a_1b_2-a_2b_1|}{2}$を示せ
＊図は動画内参照

6. f(x)=e^x sinx
(1) $0 \leqq x \leqq \pi$ y=f(x)の極大値を求めよ。

(2)x軸とy=f(x) ($0 \leqq x \leqq \pi$)で囲まれた面積を求めよ。

7. $\frac{1}{2015} , \frac{2}{2015} , \cdots , \frac{2015}{2015}$のうち既約分数の個数を求めよ。

8. $n \in \mathbb{ N }$
$2(\sqrt{n+1} - 1) < 1 + \frac{1}{\sqrt 2} + \frac{1}{\sqrt 3} + \cdots + \frac{1}{\sqrt n}$

問題文全文(内容文)：
${\large第2問}$
[1]$\triangle ABC$において、$BC=2\sqrt2$とする。$\angle ACB$の二等分線と辺$AB$の交点
を$D$とし、$CD=\sqrt2,\cos\angle BCD=\displaystyle\frac{3}{4}$とする。このとき、$BD=\boxed{\ \ ア\ \ }$
であり、

$\sin\angle ADC=\frac{\sqrt{\boxed{\ \ イウ\ \ }}}{\boxed{\ \ エ\ \ }}$

である。$\displaystyle\frac{AC}{AD}=\sqrt{\boxed{\ \ オ\ \ }}$　であるから

$AD=\boxed{\ \ カ\ \ }$

である。また、$\triangle ABC$の外接円の半径は$\displaystyle\frac{\boxed{\ \ キ\ \ }\sqrt{\boxed{\ \ ク\ \ }}}{\boxed{\ \ ケ\ \ }}$　である。

[2](1)次の$\boxed{\ \ コ\ \ },\boxed{\ \ サ\ \ }$に当てはまるものを、下の⓪～⑤のうちから
一つずつ選べ。ただし、解答の順序は問わない。

99個の観測地からなるデータがある。四分位数について述べた記述
で、どのようなデータでも成り立つものは$\boxed{\ \ コ\ \ }$と$\boxed{\ \ サ\ \ }$である。

⓪平均値は第1四分位数と第3四分位数の間にある。
①四分位範囲は標準偏差より大きい。
②中央値よりっ地裁観測地の個数は49個である。
③最大値に等しい観測値を1個削除しても第1四分位数は変わらない。
④第1四分位数より小さい観測値と、第3四分位数より大きい観測値と
をすべて削除すると、残りの観測地の個数は51個である。
⑤第1四分位数より小さい観測値と、第3四分位数より大きい観測値と
をすべて削除すると、残りの観測地からなるデータの範囲はもとの
データの四分位範囲に等しい。


(2)図1(※動画参照)は、平成27年の男の市区町村別平均寿命のデータを47の都道府県
P1,P2,$\cdots$,P47ごとに箱ひげ図にして、並べたものである。

次の$(\textrm{I}),(\textrm{II}),(\textrm{III})$は図1に関する記述である。

$(\textrm{I})$四分位範囲はどの都道府県においても1以下である。
$(\textrm{II})$箱ひげ図は中央値が小さい値から大きい値の順に上から
下へ並んである。
$(\textrm{III})$P1のデータのどの値とP47のデータのどの値とを
比較しても1.5以上の差がある。

次の$\boxed{\ \ シ\ \ }$に当てはまるものを、下の⓪～⑦のうちから一つ選べ。

$(\textrm{I}),(\textrm{II}),(\textrm{III})$の正誤の組み合わせとして正しいものは$\boxed{\ \ シ\ \ }$である。
(※選択肢は動画参照)


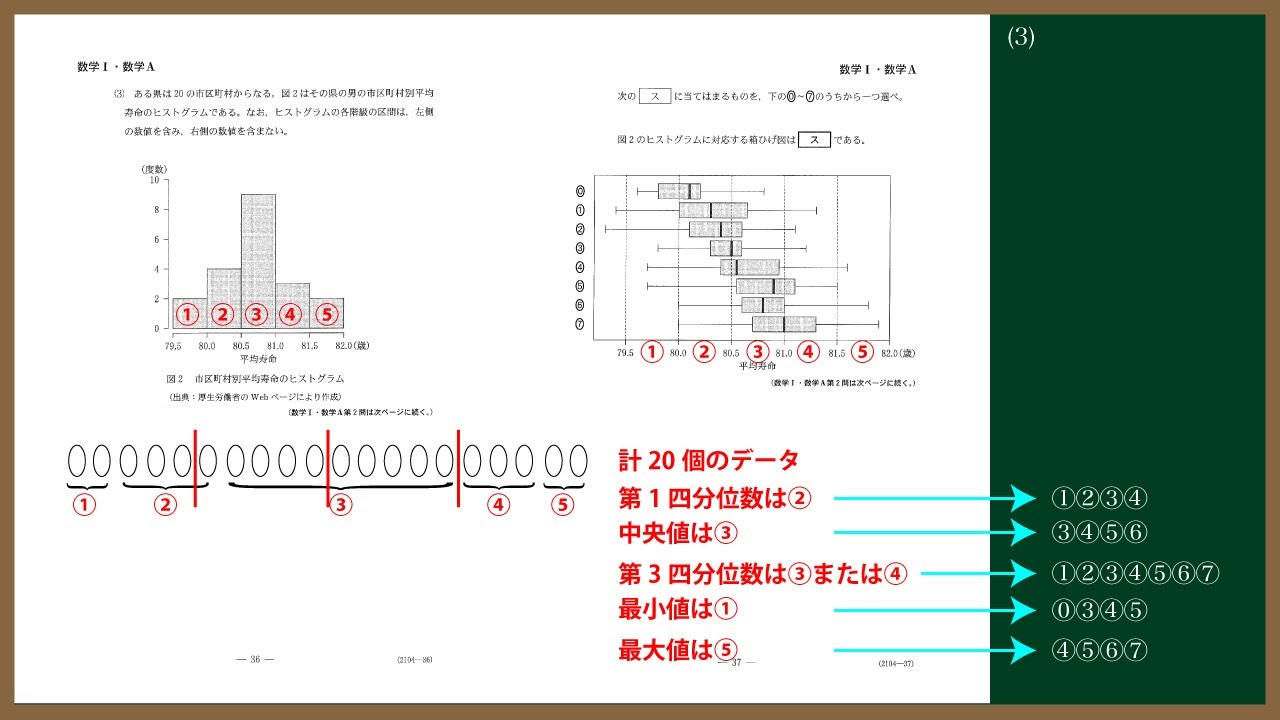
(3)ある県は20の市区町村からなる、図2(※動画参照)はその県の男の市区町村別平均
寿命のヒストグラムである。なお、ヒストグラムの各階級の区間は、左側の数値を
含み、右側の数値を含まない。

次の$\boxed{\ \ ス\ \ }$に当てはまるものを、下の⓪～⑦のうちから一つ選べ。
図2のヒストグラムに対応する箱ひげ図は$\boxed{\ \ ス\ \ }$である。
(※選択肢は動画参照)


(4)図3(※動画参照)は、平成27年の男の都道府県別平均寿命と女の都道府県別平均
寿命の散布図である。2個の点が重なって区別できないところは黒丸にしている。
図には補助的に切片が5.5から7.5まで0.5刻みで傾き1の直線を5本付加している。
次の$\boxed{\ \ セ\ \ }$に当てはまるものを、下の⓪～③のうちから一つ選べ。

都道府県ごとに男女の平均寿命の差をとったデータに対するヒストグラム
は$\boxed{\ \ セ\ \ }$である。なお、ヒストグラムの各階級の区間は、
左側の数値を含み、右側の数値を含まない。
(※選択肢は動画参照)

2020センター試験過去問

問題文全文(内容文)：
数学1A
三角比の基礎についてまとめました
基礎・対称性・正弦定理・余弦定理

問題文全文(内容文)：
正方形の対角線=10
全体の面積は？
＊図は動画内参照