【中学数学】平行線と角の問題演習～補助線の引き方～ 4-1.5【中２数学】 - 質問解決D.B.（データベース）
Generic selectors
完全一致検索
タイトルから検索
記事本文から検索
Post Type Selectors
all_unit_post
質問解決D.B.（データベース） > 動画投稿 > 数学(中学生) > 中２数学 > 平行と合同 > 【中学数学】平行線と角の問題演習～補助線の引き方～ 4-1.5【中２数学】

【中学数学】平行線と角の問題演習～補助線の引き方～ 4-1.5【中２数学】

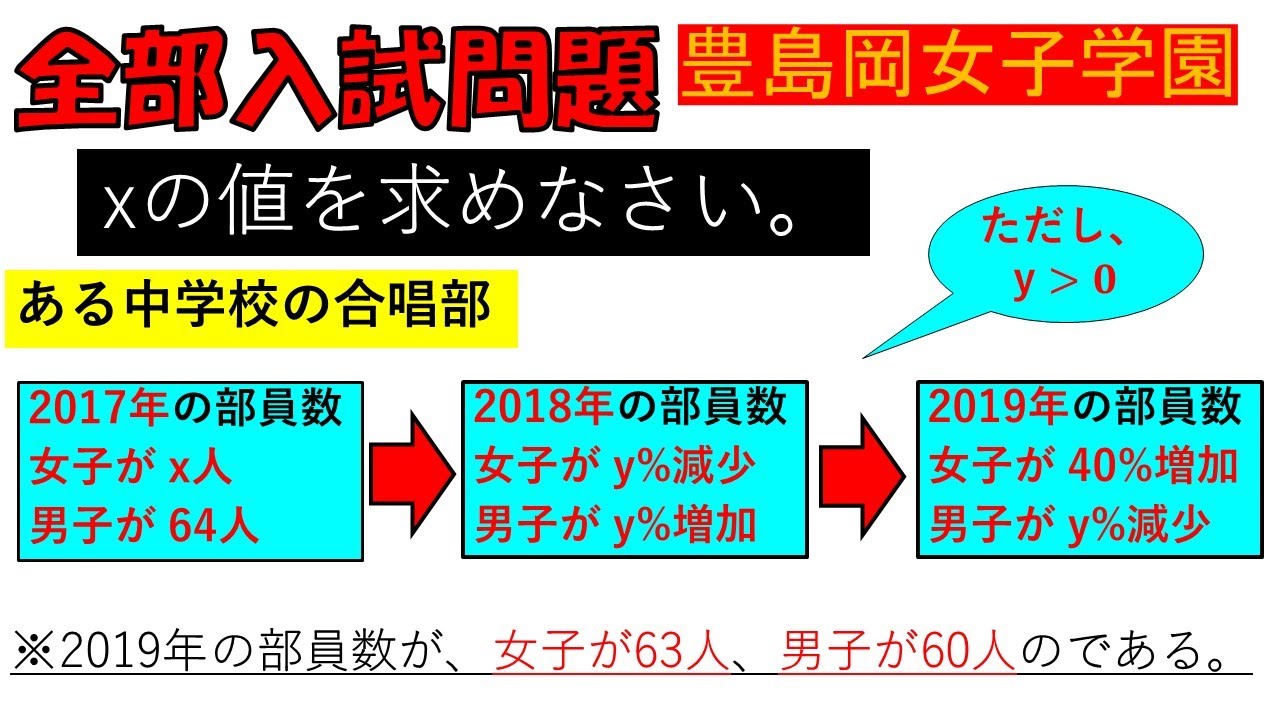
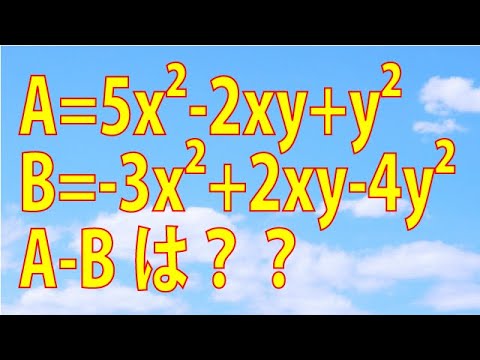問題文全文(内容文)：
平行線と角の問題演習　補助線の引き方解説動画です
チャプター：

00:00 はじまり

00:30 問題解説(1)(2)

03:08 問題解説(3)(4)

06:20 まとめ

06:43 問題と答え

単元： #数学(中学生)#中２数学#平行と合同
指導講師： 【楽しい授業動画】あきとんとん
問題文全文(内容文)：
平行線と角の問題演習　補助線の引き方解説動画です
投稿日：2021.10.24

＜関連動画＞

意外と大変！？

アイキャッチ画像
単元： #数学(中学生)#中２数学#三角形と四角形
指導講師： 数学を数楽に
問題文全文(内容文)：
x=?
＊図は動画内参照
この動画を見る　

2次関数 4S数学問題集数Ⅰ 127,128 1次関数グラフの範囲【いつものシミズ君がていねいに解説】

アイキャッチ画像
単元： #数学(中学生)#中２数学#数Ⅰ#２次関数#1次関数#2次関数とグラフ#数学(高校生)
教材： #4S数学#4S数学Ⅰ＋AのB問題解説（新課程2022年以降）#2次関数#中高教材
指導講師： 理数個別チャンネル
問題文全文(内容文)：
【1】次の条件を満たすように、定数$a,b$の値を求めよ
（１）$y=ax+b$が$x=-2$のとき$y=5$,$x＝1$のとき$y=2$
（２）$y=ax+b$が$(-1,-1)(3,1)$を通る

【2】次の条件を満たすように、定数$a,b$の値を求めよ
（１）$y=3x+b(0\leqq x\leqq 4)$の地域が$1\leqq y\leqq 19$である
（２）$y=ax+b(1\leqq x\leqq 3)$の地域が$0\leqq y\leqq 1$である
ただし$a\lt 0$である.
この動画を見る　

正八角形　　大阪教育大学附属天王寺　予告問題Fが一個多かったです。申し訳ございませんでした。

アイキャッチ画像
単元： #数学(中学生)#中２数学#三角形と四角形#高校入試過去問(数学)
指導講師： 数学を数楽に
問題文全文(内容文)：
正八角形
斜線部の面積を求めよ
＊図は動画内参照

大阪教育大学附属高等学校天王寺校舎
この動画を見る　

連立方程式

アイキャッチ画像
単元： #連立方程式#数Ⅱ#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#数学(高校生)
指導講師： 鈴木貫太郎
問題文全文(内容文)：
これを解け.

{$\dfrac{ab}{a+b}=1$
{$\dfrac{bc}{b+c}=2$
{$\dfrac{ca}{c+a}=3$
この動画を見る　

【中学数学】連立方程式の代入法をどこよりも丁寧に教えます 2-1【中２数学】

アイキャッチ画像
単元： #中２数学#連立方程式
指導講師： 【楽しい授業動画】あきとんとん
問題文全文(内容文)：
連立方程式の代入法解説動画です
この動画を見る　
PAGE TOP