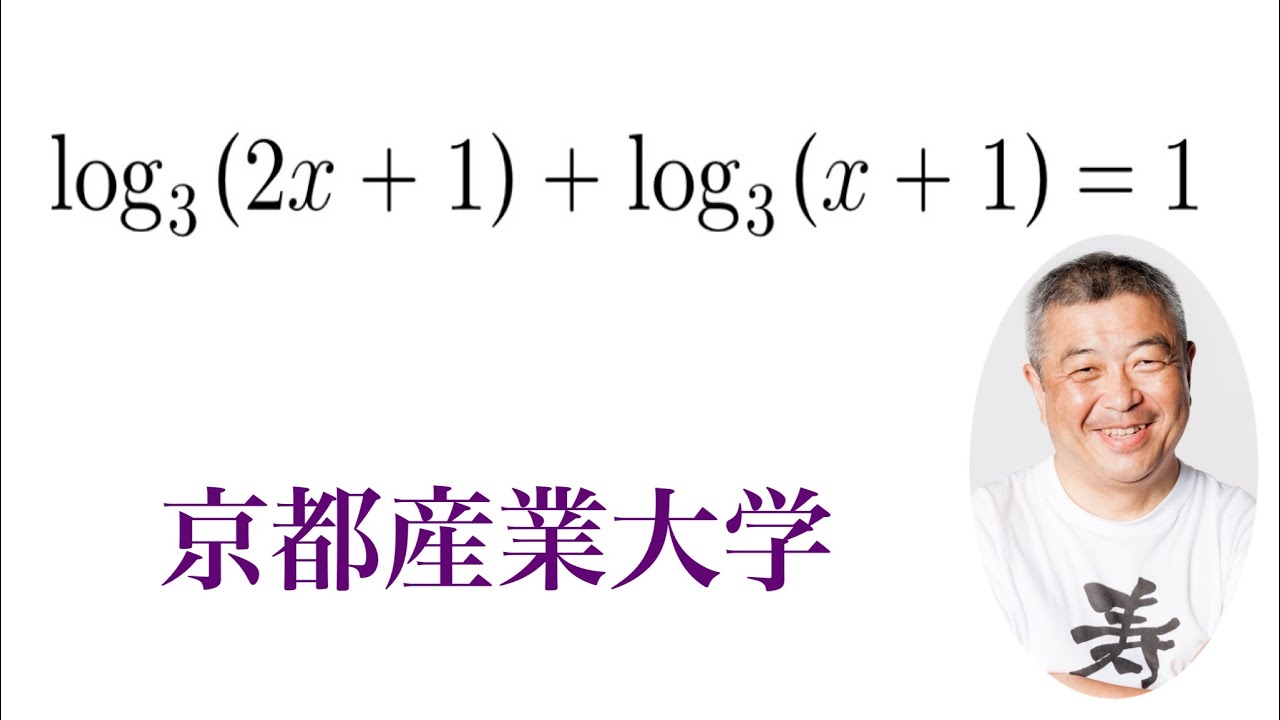【数学II】必殺！完璧攻略法！「小数第何位に初めて0でない数字が表れるか」

問題文全文(内容文)：
$\displaystyle \frac{1}{2}^{10}$は小数第何位に初めて0でない数字が表れるか。
$log_{ 10 }2=0.3010$とする。

単元： #数Ⅱ#指数関数と対数関数#対数関数#数学(高校生)

指導講師：カサニマロ【べんとう・ふきのとうの授業動画】

問題文全文(内容文)：
$\displaystyle \frac{1}{2}^{10}$は小数第何位に初めて0でない数字が表れるか。
$log_{ 10 }2=0.3010$とする。

投稿日：2019.06.07

単元： #数A#数Ⅱ#整数の性質#約数・倍数・整数の割り算と余り・合同式#指数関数と対数関数#対数関数#数学(高校生)

指導講師：鈴木貫太郎

問題文全文(内容文)：
$log_{5832}n$が有理数で$\displaystyle \frac{1}{2} \lt log_{5832}n \lt 1$である自然数$n$を求めよ

出典：群馬大学医学部　過去問

この動画を見る　

単元： #数Ⅱ#指数関数と対数関数#対数関数#数学(高校生)

指導講師：鈴木貫太郎

問題文全文(内容文)：
これを簡単にせよ.$a,b,c$を正とし,$a,b,c \neq 1$である.
$\dfrac{1}{1+\log_a bc}+\dfrac{1}{1+\log_b ca}+\dfrac{1}{1+\log_c ab}$

この動画を見る　

単元： #数Ⅱ#指数関数と対数関数#対数関数#数列#漸化式#数学(高校生)#数B

指導講師：鈴木貫太郎

問題文全文(内容文)：
数列$a_n,a_1=5,a_{n+1}=2,a_n+3^n$がある.

(1)$a_n$を求めよ.
(2)$a_n\lt 10^{10}$を満たす最大の$n$を求めよ.
$\log_{10}2=0.3010,\log_{10}3=0.4771$

1998一橋大過去問

この動画を見る　

単元： #数Ⅱ#大学入試過去問(数学)#指数関数と対数関数#対数関数#学校別大学入試過去問解説(数学)#数学(高校生)#広島大学

指導講師：鈴木貫太郎

問題文全文(内容文)：
（1）
$log_{2}3$は無理数、証明せよ

（2）
$p,q$は異なる自然数
$p$ $log_{2}3$と$q$ $log_{2}3$の小数部分は異なる。
証明せよ

（3）
$log_{2}3$の小数第一位の数を求めよ

出典：広島大学　過去問

この動画を見る　

単元： #数Ⅱ#指数関数と対数関数#対数関数#数学(高校生)

指導講師：鈴木貫太郎

問題文全文(内容文)：
$ (2+3)(2^2+3^2)(2^4+3^4)(2^8+3^8)(2^{16}+3^{16})(2^{32}+3^{32})と,3^{64}はどちらが大きいか?$

この動画を見る　