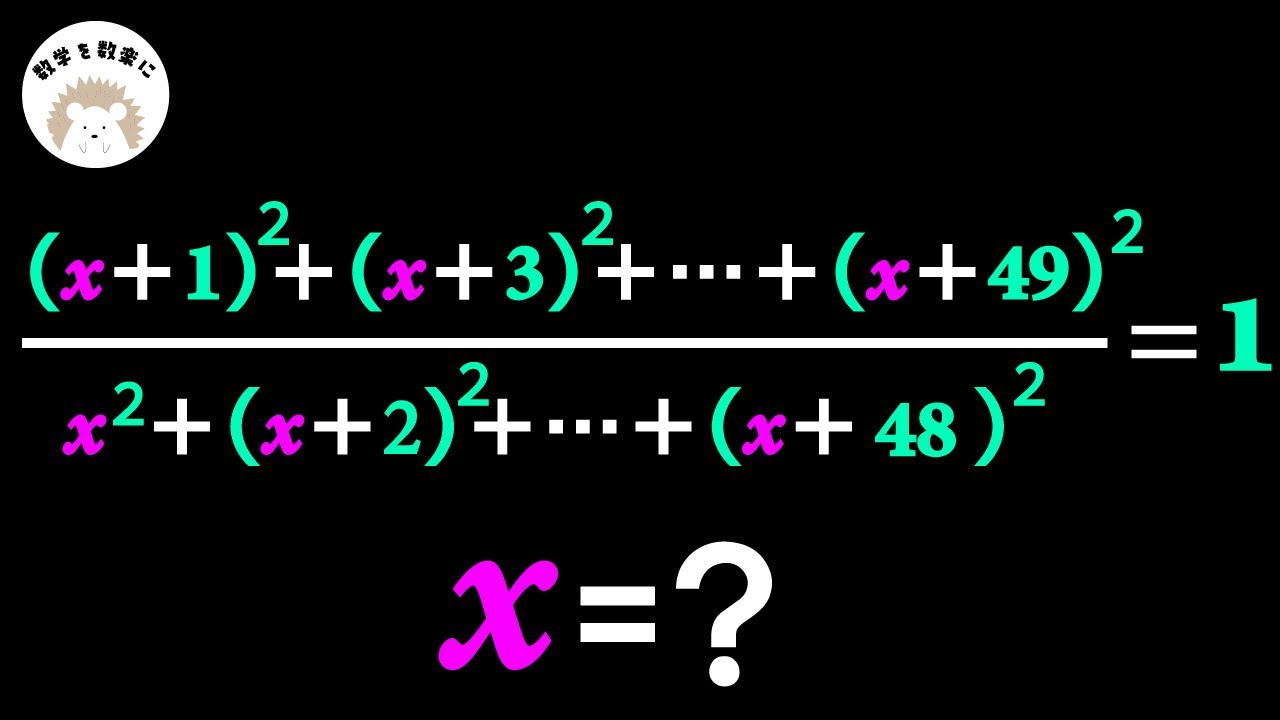【不定方程式の特解はこれで楽勝】合同式を使った不定方程式の解き方を解説！〔数学高校数学〕

問題文全文(内容文)：
合同式を使った不定方程式の解き方について解説します。

単元： #数A#整数の性質#ユークリッド互除法と不定方程式・Ｎ進法#数学(高校生)

指導講師： 3rd School

問題文全文(内容文)：
合同式を使った不定方程式の解き方について解説します。

投稿日：2022.04.06

単元： #数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#数学(高校生)#産業医科大学

指導講師：ますただ

問題文全文(内容文)：
$\dfrac{b^2}{a}+\dfrac{a}{b}=6$を満たす
自然数の組$(a,b)$のうち$a+b$の最小値を求めよ.

2024産業医科大学過去問題

この動画を見る　

単元： #数A#整数の性質#ユークリッド互除法と不定方程式・Ｎ進法#数学(高校生)

指導講師：鈴木貫太郎

問題文全文(内容文)：
これを解け.
$(2+\sqrt3)^{x^2}=(7-4\sqrt3)^{x-4}$

この動画を見る　

単元： #数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)

指導講師：鈴木貫太郎

問題文全文(内容文)：
$a+b+c-2,ab+bc+ca=3,abc=2$である.
$a^5+b^5+c^5$の値を求めよ.

2012名古屋市立大過去問

この動画を見る　

単元： #数A#整数の性質#ユークリッド互除法と不定方程式・Ｎ進法#数学(高校生)

指導講師：数学を数楽に

問題文全文(内容文)：
x=?
$9^x = 27$

この動画を見る　

単元： #数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)

指導講師：理数個別チャンネル

問題文全文(内容文)：
【高校数学　数学A　場合の数と確率】
12の正の約数の個数とその総和を求めよ。
（出典元）４STEP数学Aより

この動画を見る　