 整数の性質
整数の性質
 整数の性質
整数の性質
大学入試問題#869「次数は分子の方が高いのね」 #玉川大学(2022) #整数問題

単元:
#数A#大学入試過去問(数学)#整数の性質#学校別大学入試過去問解説(数学)#数学(高校生)
指導講師:
問題文全文(内容文):
$\displaystyle \frac{12n^2+13n+51}{3n+1}$が整数となるような整数$n$をすべて求めよ。
出典:2022年玉川大学 入試問題
この動画を見る
$\displaystyle \frac{12n^2+13n+51}{3n+1}$が整数となるような整数$n$をすべて求めよ。
出典:2022年玉川大学 入試問題
大学入試問題#912「解答を綺麗にする時間がなかった」 #自治医科大学2024

単元:
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#数学(高校生)#自治医科大学
指導講師:
ますただ
問題文全文(内容文):
$0 \leq k:$整数
$N=\displaystyle \frac{k^2+k+300}{k^3+k^2+2k+2}$が自然数となるときのすべての$k$の値の和$S$を求めよ。
出典:2024年自治医科大学
この動画を見る
$0 \leq k:$整数
$N=\displaystyle \frac{k^2+k+300}{k^3+k^2+2k+2}$が自然数となるときのすべての$k$の値の和$S$を求めよ。
出典:2024年自治医科大学
大学入試問題#911「私学医学部では出題必須か!?」 #自治医科大学2024

単元:
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#数学(高校生)#自治医科大学
指導講師:
ますただ
問題文全文(内容文):
実数$x,y$が$x^2+y^2=1$を満たすとき、$5x^2+4xy+y^2$の最大値を$M,$最小値を$m$とする。
$\displaystyle \frac{(M-m)^2}{4}$の値を求めよ。
出典:2024年自治医科大学
この動画を見る
実数$x,y$が$x^2+y^2=1$を満たすとき、$5x^2+4xy+y^2$の最大値を$M,$最小値を$m$とする。
$\displaystyle \frac{(M-m)^2}{4}$の値を求めよ。
出典:2024年自治医科大学
大学入試問題#906「色んな要素がモリモリ問題」昭和大学医学部(2012)

単元:
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#数学(高校生)#昭和大学
指導講師:
ますただ
問題文全文(内容文):
正の数$a,b$が$a^3+b^3=5$を満たすとき、$a+b$のとりうる値の範囲を求めよ。
出典:2012年昭和大学医学部
この動画を見る
正の数$a,b$が$a^3+b^3=5$を満たすとき、$a+b$のとりうる値の範囲を求めよ。
出典:2012年昭和大学医学部
大学入試問題#897「解法の迷走」 #北海道大学(2024)

単元:
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#数学(高校生)#北海道大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \frac{x^2-x+1}{x^2+x+1}$
が整数となるような実数$x$をすべて求めよ。
出典:2024年北海道大学後期
この動画を見る
$\displaystyle \frac{x^2-x+1}{x^2+x+1}$
が整数となるような実数$x$をすべて求めよ。
出典:2024年北海道大学後期
大学入試問題#885「油断したら沼るかも」 #奈良県立医科大学(2014) 三角関数と整数問題
単元:
#数A#数Ⅱ#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#三角関数#学校別大学入試過去問解説(数学)#数学(高校生)#奈良県立医科大学
指導講師:
ますただ
問題文全文(内容文):
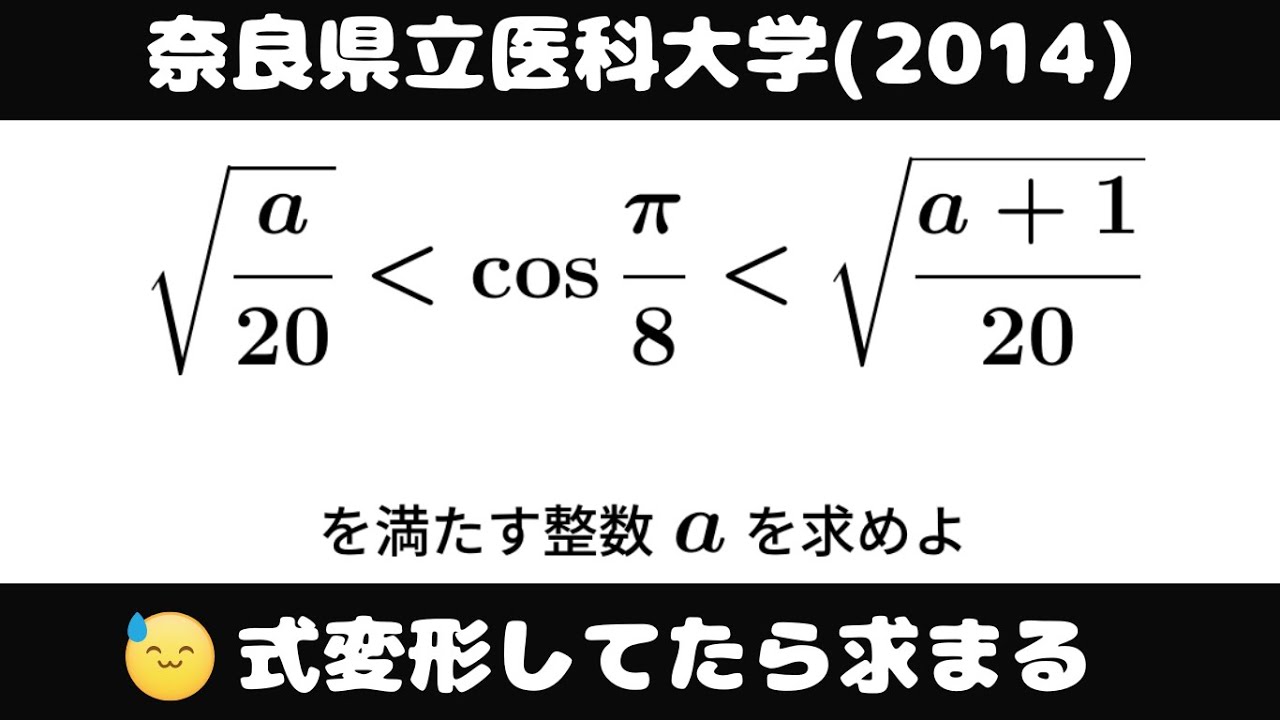
$\sqrt{ \displaystyle \frac{a}{20} } \lt \cos\displaystyle \frac{\pi}{8} \lt \sqrt{ \displaystyle \frac{a+1}{20} }$を満たす整数$a$を求めよ。
出典:2014年奈良県立医科大学
この動画を見る
$\sqrt{ \displaystyle \frac{a}{20} } \lt \cos\displaystyle \frac{\pi}{8} \lt \sqrt{ \displaystyle \frac{a+1}{20} }$を満たす整数$a$を求めよ。
出典:2014年奈良県立医科大学
方程式
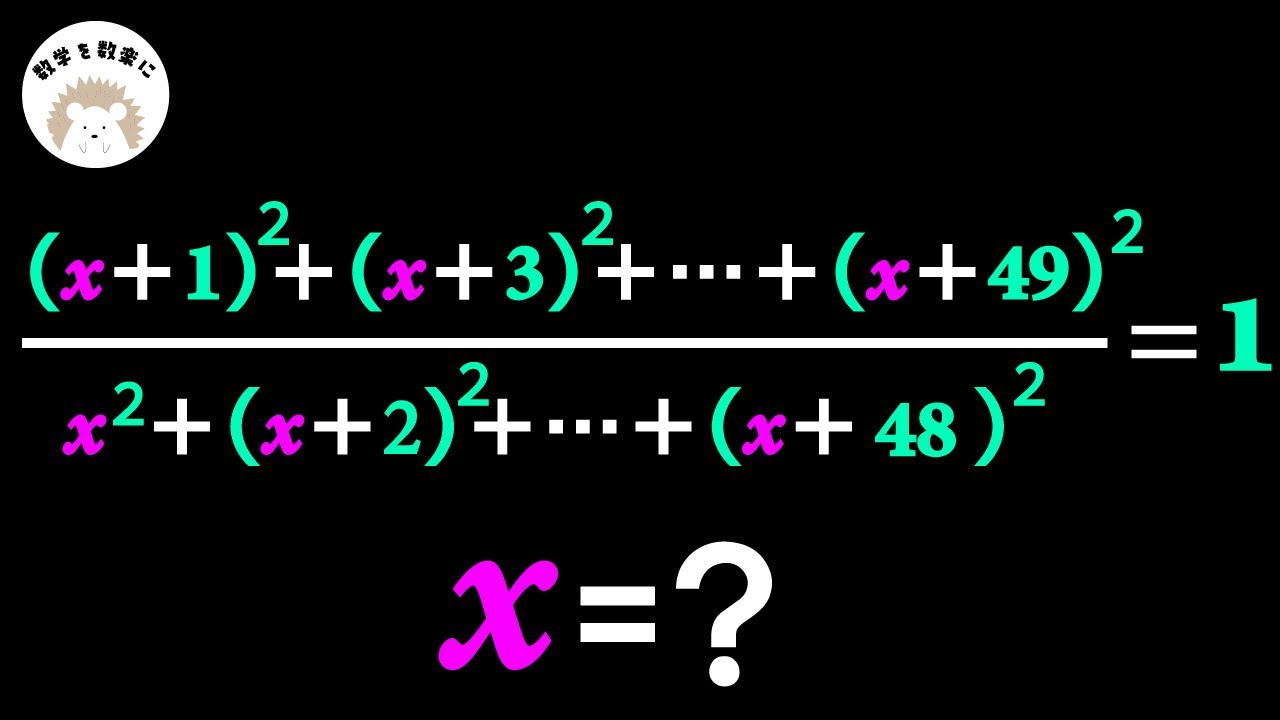
単元:
#数A#整数の性質#ユークリッド互除法と不定方程式・N進法#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$\frac{(x+1)^2+(x+3)^2+(x+5)^2+ \cdots +(x+49)^2}{x^2+(x+2)^2+(x+4)^2+ \cdots +(x+48)^2}=1$
この動画を見る
$\frac{(x+1)^2+(x+3)^2+(x+5)^2+ \cdots +(x+49)^2}{x^2+(x+2)^2+(x+4)^2+ \cdots +(x+48)^2}=1$
いやらしい方程式を解け!!

単元:
#数A#整数の性質#ユークリッド互除法と不定方程式・N進法#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
方程式を解け
(1)$x=x$
(2)$x=x+1$
この動画を見る
方程式を解け
(1)$x=x$
(2)$x=x+1$
整数問題 城北高校

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
20以下の自然数nのうち
$(n+1)^2+(n+3)^2+(n+5)^2$が7の倍数となるものは何個?
城北高等学校
この動画を見る
20以下の自然数nのうち
$(n+1)^2+(n+3)^2+(n+5)^2$が7の倍数となるものは何個?
城北高等学校
整数問題 修道高校

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
n(n+1)が88の倍数になるような正の整数nのうち最小のものは?
修道高等学校
この動画を見る
n(n+1)が88の倍数になるような正の整数nのうち最小のものは?
修道高等学校
【高校数学】整数の性質 方程式の問題ではこうやって範囲を絞り込もう!

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
方程式$xy+yz+zx=xyz$を満たす自然数
$x,y,z$の組をすべて求めよ。
この動画を見る
方程式$xy+yz+zx=xyz$を満たす自然数
$x,y,z$の組をすべて求めよ。
【高校数学】整数の性質 約数の総和に関する問題はこうやって解く!

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
$N=p^2q$($p,q$は異なる素数)と表される数で
約数の総和が$2N$に等しいものをすべて求めよ。
この動画を見る
$N=p^2q$($p,q$は異なる素数)と表される数で
約数の総和が$2N$に等しいものをすべて求めよ。
整数問題
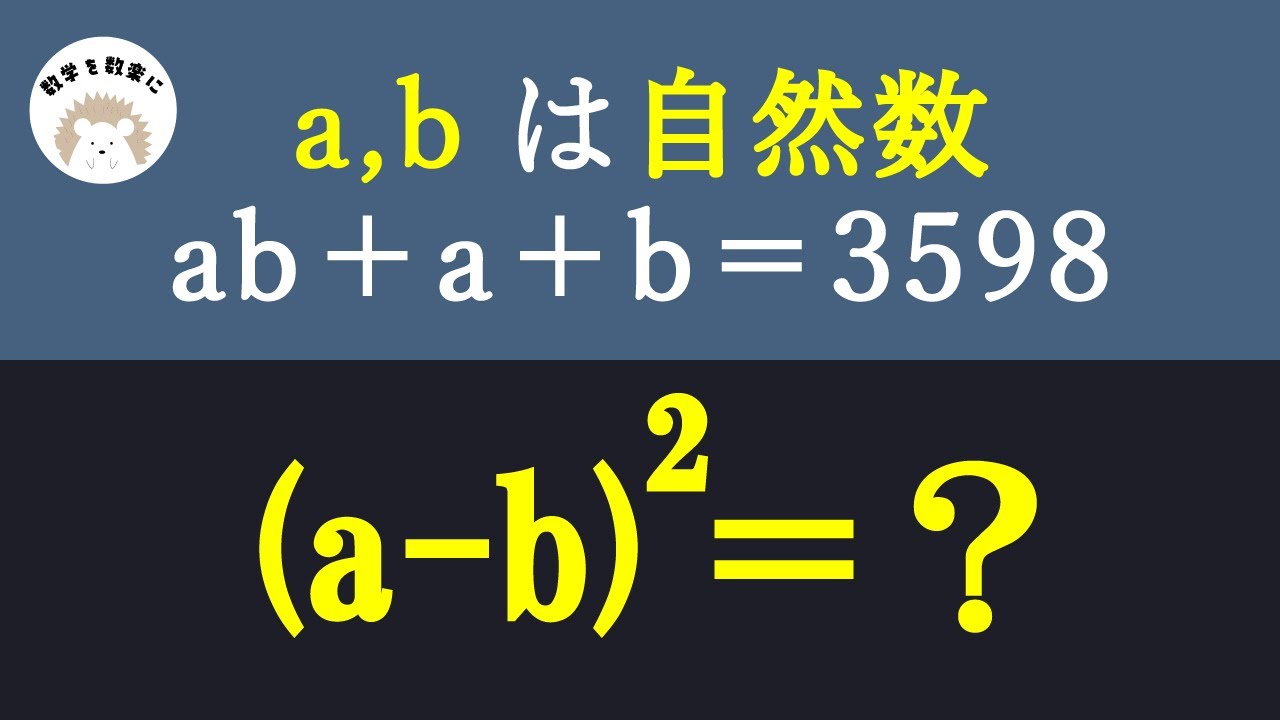
単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
a,bは自然数
ab+a+b=3598
$(a-b)^2=?$
この動画を見る
a,bは自然数
ab+a+b=3598
$(a-b)^2=?$
約数の個数とその総和 2024明大中野

単元:
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
・正の約数を3個だけ持つ
・その約数の総和は871
この自然数を求めよ。
2024明治大学付属中野高等学校
この動画を見る
・正の約数を3個だけ持つ
・その約数の総和は871
この自然数を求めよ。
2024明治大学付属中野高等学校
2024山口大 1の10乗根のナイスな問題

単元:
#数Ⅰ#数A#大学入試過去問(数学)#図形と計量#三角比への応用(正弦・余弦・面積)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$2Z^4+(1-\sqrt{ 5 })Z^2+2=0$であるとき
(1)$Z^{10}=1$であることを示せ
(2)$\cos \displaystyle \frac{\pi}{5} \cos \displaystyle \frac{2\pi}{5}=\displaystyle \frac{1}{4}$を示せ
出典:2024年山口大学数学 過去問
この動画を見る
$2Z^4+(1-\sqrt{ 5 })Z^2+2=0$であるとき
(1)$Z^{10}=1$であることを示せ
(2)$\cos \displaystyle \frac{\pi}{5} \cos \displaystyle \frac{2\pi}{5}=\displaystyle \frac{1}{4}$を示せ
出典:2024年山口大学数学 過去問
一橋の問題をちょっと変えてみた

単元:
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$m,n$正の整数
$100m^2-49n^2=20!$を満たす$(m,n)$の組は何組?
この動画を見る
$m,n$正の整数
$100m^2-49n^2=20!$を満たす$(m,n)$の組は何組?
2024一橋大後期数学 整数問題

単元:
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$m,n$正の整数
$m^2-n^2=10!$を満たす$(m,n)$の組は何組?
出典:2024年一橋大学後期数学 過去問
この動画を見る
$m,n$正の整数
$m^2-n^2=10!$を満たす$(m,n)$の組は何組?
出典:2024年一橋大学後期数学 過去問
京都大 2024文系数学

単元:
#数A#大学入試過去問(数学)#整数の性質#ユークリッド互除法と不定方程式・N進法#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
ある自然数を八進法,九進法,十進法で表したら桁数が同じ最大の自然数は?
$0.3010<\log_{10}{3}<0.3011$
$0.4771<\log_{10}{2}<0.4772$
2024京都大過去問
この動画を見る
ある自然数を八進法,九進法,十進法で表したら桁数が同じ最大の自然数は?
$0.3010<\log_{10}{3}<0.3011$
$0.4771<\log_{10}{2}<0.4772$
2024京都大過去問
東大 文系数学 2024
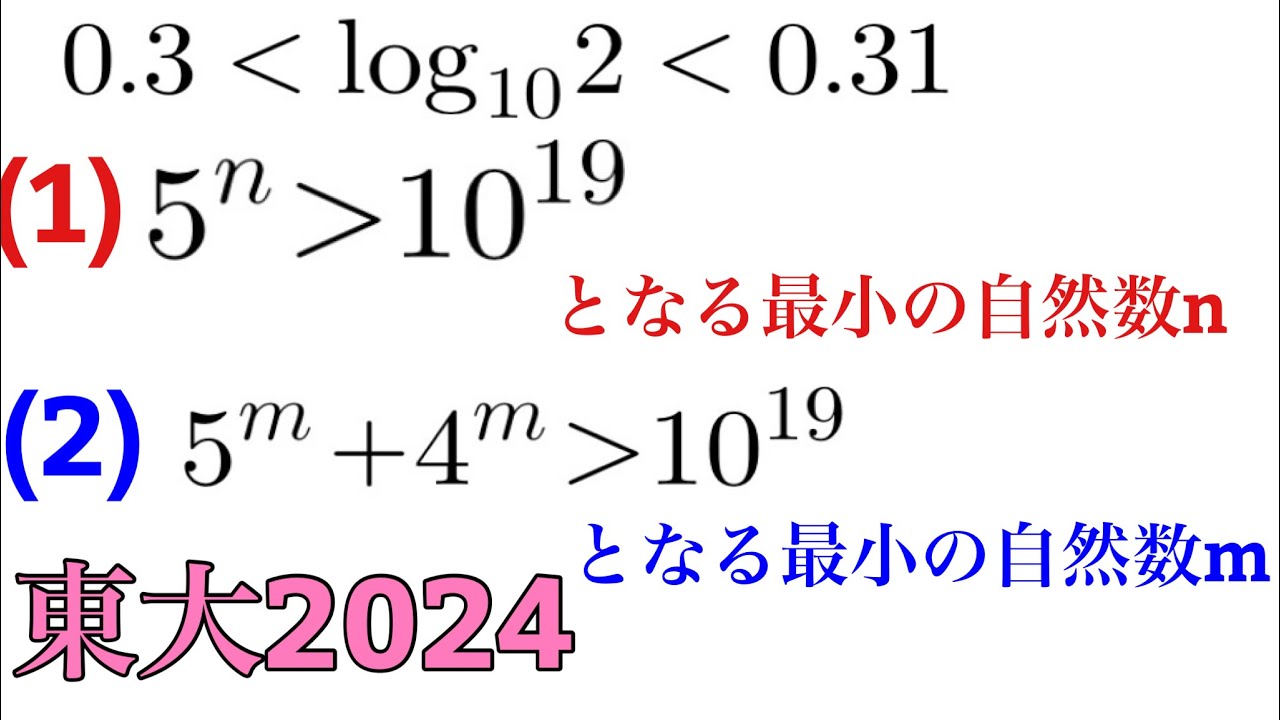
単元:
#数A#大学入試過去問(数学)#整数の性質#ユークリッド互除法と不定方程式・N進法#学校別大学入試過去問解説(数学)#東京大学#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$0.3<\log_{10}{2}<0.31$
を用いてよい
(1)$5^n>10^{19}$
となる最小の自然数n
(2)$5^m+4^m>10^{19}$
となる最小の自然数m
2024東大文系過去問
この動画を見る
$0.3<\log_{10}{2}<0.31$
を用いてよい
(1)$5^n>10^{19}$
となる最小の自然数n
(2)$5^m+4^m>10^{19}$
となる最小の自然数m
2024東大文系過去問
2024 慶應女子最初の一問 整数問題

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$a^2+b^2-2a-4b=20$を満たす
自然数(a,b)の組をすべて求めよ
2024慶應義塾女子高等学校
この動画を見る
$a^2+b^2-2a-4b=20$を満たす
自然数(a,b)の組をすべて求めよ
2024慶應義塾女子高等学校
福田の数学〜慶應義塾大学2024年理工学部第1問(1)〜6番目に大きい約数と6乗根に最も近い自然数

単元:
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\boxed{1}$(1)2024の約数の中で1番大きいものは2024だが,6番目に大きいものは$\boxed{ア}$である.
2024の6乗根に最も近い自然数は$\boxed{イ}$である.
2024慶應義塾大学理工過去問
この動画を見る
$\boxed{1}$(1)2024の約数の中で1番大きいものは2024だが,6番目に大きいものは$\boxed{ア}$である.
2024の6乗根に最も近い自然数は$\boxed{イ}$である.
2024慶應義塾大学理工過去問
福田のおもしろ数学055〜自然数を連続整数の和で表す方法〜偶奇性に注目しよう

福田の数学〜慶應義塾大学2024年理工学部第1問(1)〜6番目に大きい約数と6乗根に最も近い自然数

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#指数関数と対数関数#指数関数#対数関数#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
( 1 ) 2024 の約数の中で 1 番大きいものは 2024 だが、 6 番目に大きいものは ア である。 2024 の 6 乗根に最も近い自然数は イ である。
この動画を見る
( 1 ) 2024 の約数の中で 1 番大きいものは 2024 だが、 6 番目に大きいものは ア である。 2024 の 6 乗根に最も近い自然数は イ である。
整数の問題& 場合の数 2024早稲田実業

単元:
#数A#大学入試過去問(数学)#場合の数と確率#整数の性質#場合の数#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
1⃣2⃣3⃣4⃣の4枚のカードを
$▢^▢×▢▢$のように並べる
式の値が3の倍数となる並べ方は何通り?
2024早稲田実業学校
この動画を見る
1⃣2⃣3⃣4⃣の4枚のカードを
$▢^▢×▢▢$のように並べる
式の値が3の倍数となる並べ方は何通り?
2024早稲田実業学校
綺麗な問題。それしかないことを示すのが肝

2進法ののび太ってなに?

単元:
#数A#整数の性質#ユークリッド互除法と不定方程式・N進法#数学(高校生)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
二進法ののび太を使って二進法の原理を解説をします。
この動画を見る
二進法ののび太を使って二進法の原理を解説をします。
福田のおもしろ数学052〜余りの問題はこれができなきゃダメ〜余りを求める

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$1111^{ 2018 }$ を 11111 で割った余りを求めてください。
この動画を見る
$1111^{ 2018 }$ を 11111 で割った余りを求めてください。
整数部分 2024灘高校の最初の1問

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$\sqrt {15} + \sqrt{10} $の整数部分は?
灘高等学校2024
この動画を見る
$\sqrt {15} + \sqrt{10} $の整数部分は?
灘高等学校2024
福田の数学〜東京大学2018年理系第2問〜数列の増減とユークリッドの互除法

単元:
#数A#大学入試過去問(数学)#整数の性質#ユークリッド互除法と不定方程式・N進法#数列#漸化式#学校別大学入試過去問解説(数学)#東京大学#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
$a_{ 1 },a_{ 2 }・・・$を
$a_{ n }=\dfrac{2_{ n }+{}_1 \mathrm{ C }_n}{n!}$(n=1,2,・・・)
で定める
(1)$n \geqq 2$とする。$\dfrac{a_{n}}{a_{n-1}}$を規約分数$\dfrac{q_{n}}{p_{n}}$として表したときの分母$p_{n} \geqq 1$と分子$q_{n}$を求めよ。
(2)$a_{n}$が整数となる$n\geqq1$をすべて求めよ。
2018東京大学理過去問
この動画を見る
$a_{ 1 },a_{ 2 }・・・$を
$a_{ n }=\dfrac{2_{ n }+{}_1 \mathrm{ C }_n}{n!}$(n=1,2,・・・)
で定める
(1)$n \geqq 2$とする。$\dfrac{a_{n}}{a_{n-1}}$を規約分数$\dfrac{q_{n}}{p_{n}}$として表したときの分母$p_{n} \geqq 1$と分子$q_{n}$を求めよ。
(2)$a_{n}$が整数となる$n\geqq1$をすべて求めよ。
2018東京大学理過去問
福田のおもしろ数学047〜これができたら天才〜ガウス記号のついた数の和
単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数列#数列とその和(等差・等比・階差・Σ)#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
$[\dfrac{13×1}{2024}]+[\dfrac{13×2}{2024}]+[\dfrac{13×3}{2024}]+・・・+[\dfrac{13×2023}{2024}]$を計算してください。
ただし、$[x]$は$x$を超えない最大の整数を表します。
この動画を見る
$[\dfrac{13×1}{2024}]+[\dfrac{13×2}{2024}]+[\dfrac{13×3}{2024}]+・・・+[\dfrac{13×2023}{2024}]$を計算してください。
ただし、$[x]$は$x$を超えない最大の整数を表します。
