問題文全文(内容文):
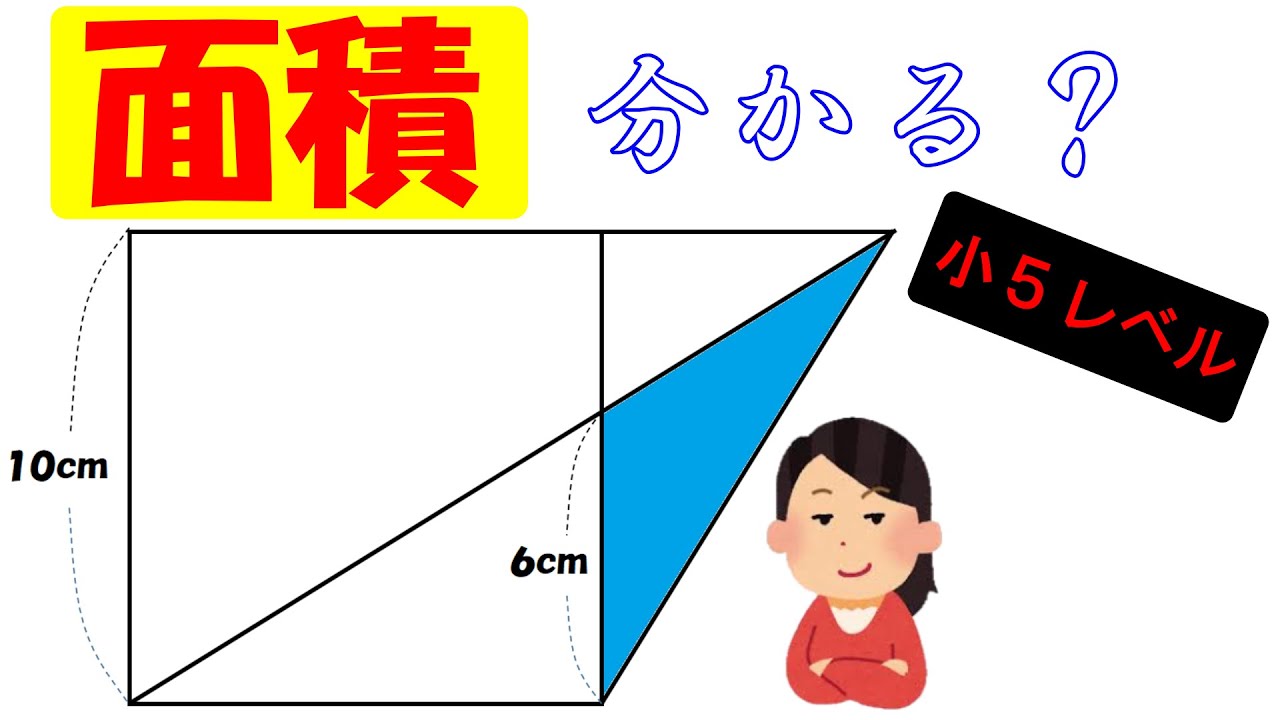
・左図は、1辺が6㎝の正方形と1辺が4㎝の正方形をつなげたものです。三角形ABCの面積は?
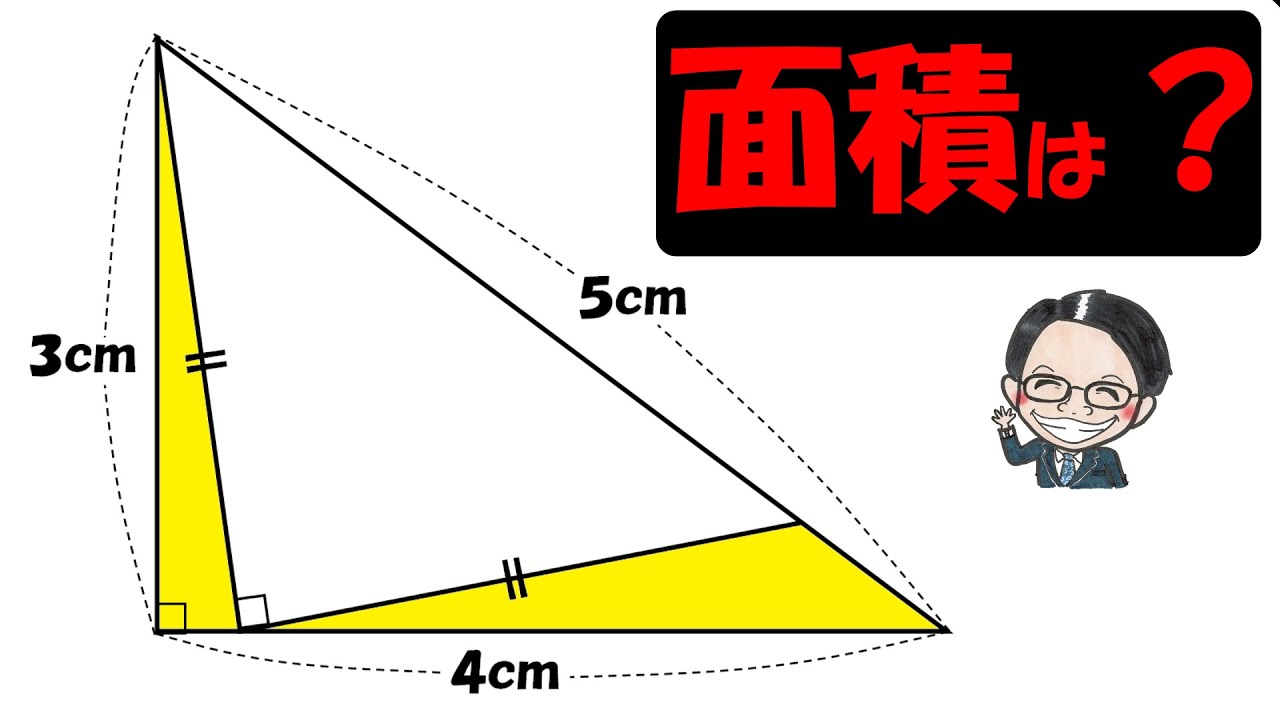
・左図において、AB、CEは8㎝、○印をつけた角の大きさは等しい。
このとき、四角形ACDEの面積は三角形ABCの面積の何倍?
*図は動画内参照
・左図は、1辺が6㎝の正方形と1辺が4㎝の正方形をつなげたものです。三角形ABCの面積は?
・左図において、AB、CEは8㎝、○印をつけた角の大きさは等しい。
このとき、四角形ACDEの面積は三角形ABCの面積の何倍?
*図は動画内参照
単元:
#算数(中学受験)#過去問解説(学校別)#平面図形#角度と面積#灘中学校
指導講師:
こばちゃん塾
問題文全文(内容文):
・左図は、1辺が6㎝の正方形と1辺が4㎝の正方形をつなげたものです。三角形ABCの面積は?
・左図において、AB、CEは8㎝、○印をつけた角の大きさは等しい。
このとき、四角形ACDEの面積は三角形ABCの面積の何倍?
*図は動画内参照
・左図は、1辺が6㎝の正方形と1辺が4㎝の正方形をつなげたものです。三角形ABCの面積は?
・左図において、AB、CEは8㎝、○印をつけた角の大きさは等しい。
このとき、四角形ACDEの面積は三角形ABCの面積の何倍?
*図は動画内参照
投稿日:2021.09.08