早稲田実業高円の性質・角の二等分線の定理 - 質問解決D.B.（データベース）

問題文全文(内容文)：
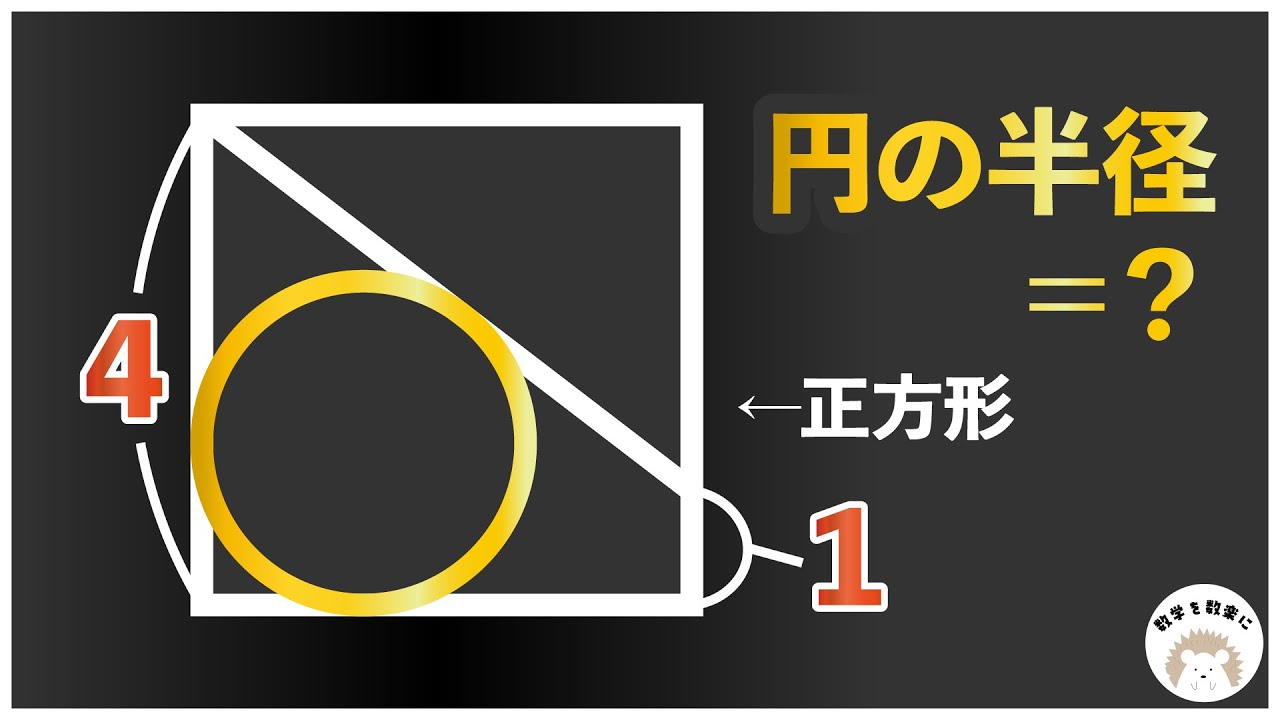
(1)半円の半径を求めよ.
(2)$AD$の長さを求めよ.
(3)$\triangle ADE$の長さを求めよ.

早稲田実業高過去問

単元： #数Ⅰ#図形と計量#三角比（三角比・拡張・相互関係・単位円）#数学(高校生)

指導講師：鈴木貫太郎

問題文全文(内容文)：
(1)半円の半径を求めよ.
(2)$AD$の長さを求めよ.
(3)$\triangle ADE$の長さを求めよ.

早稲田実業高過去問

投稿日：2021.05.26

単元： #数Ⅰ#数と式#集合と命題（集合・命題と条件・背理法）#数学(高校生)

指導講師：福田次郎

問題文全文(内容文)：
数学$\textrm{I}$　必要条件・十分条件
$a \gt 0$とする。2つの条件$p,q$を
$p:|x-1| \leqq a,　q:|x| \lt 2$とする。
(1)$p$が$q$の十分条件となる$a$の範囲
(2)$p$が$q$の必要条件となる$a$の範囲

この動画を見る　

単元： #数Ⅰ#図形と計量#三角比への応用（正弦・余弦・面積）#数学(高校生)

教材： #4S数学#4S数学Ⅰ＋AのB問題解説（新課程2022年以降）#図形と計量#中高教材

指導講師：理数個別チャンネル

問題文全文(内容文)：
次のような平行四辺形ABCDの面積を求めよ。
(1)AB=3、BC=5、∠ABC=60°
(2)AB=4、AD=6、∠ABC=135°

この動画を見る　

単元： #数Ⅰ#数と式#集合と命題（集合・命題と条件・背理法）#数学(高校生)

指導講師：ハクシ高校【数学科】良問演習チャンネル

問題文全文(内容文)：
次の問いに答えよ。
（1）
$mn$が偶数ならば、$m,n$のうち少なくとも1つは偶数であることを示せ。
ただし、$m,n$は整数とする。

（2）
$\sqrt{ 2 }$が無理数であることを示せ。

この動画を見る　

単元： #数学(中学生)#数Ⅰ#数と式#実数と平方根（循環小数・有理数・無理数・絶対値・平方根計算・2重根号）#高校入試過去問(数学)#数学(高校生)

指導講師：数学を数楽に

問題文全文(内容文)：
$1.\dot{2} \dot{3}$を分数で表せ。

近江高等学校

この動画を見る　

単元： #数学(中学生)#数と式

指導講師：鈴木貫太郎

問題文全文(内容文)：
$ x^2+y^2+xy=133,x+y+\sqrt{xy}-1$
これを解け.

この動画を見る　