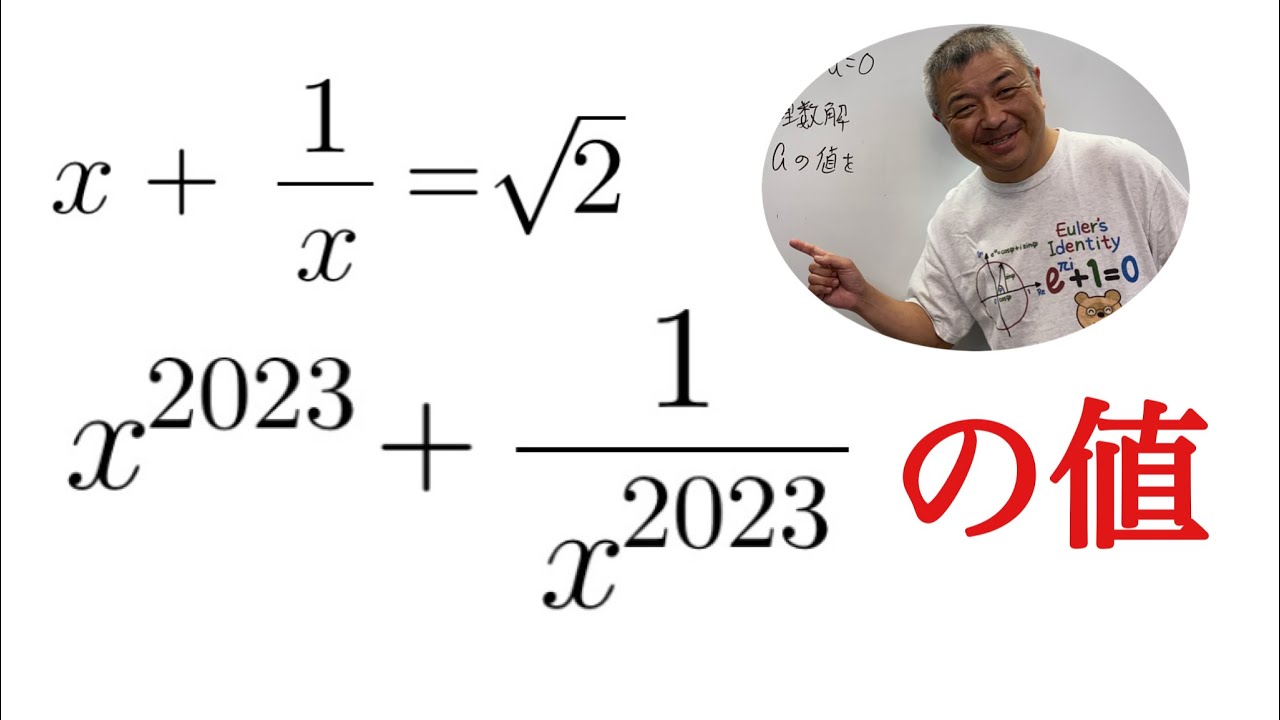問題文全文(内容文):
$4Z^2+4Z-\sqrt3 i=0$の2つの解の複素数平面上の距離を求めよ.
慶應(医)過去問
$4Z^2+4Z-\sqrt3 i=0$の2つの解の複素数平面上の距離を求めよ.
慶應(医)過去問
単元:
#大学入試過去問(数学)#複素数平面#複素数平面#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)#数C
指導講師:
鈴木貫太郎
問題文全文(内容文):
$4Z^2+4Z-\sqrt3 i=0$の2つの解の複素数平面上の距離を求めよ.
慶應(医)過去問
$4Z^2+4Z-\sqrt3 i=0$の2つの解の複素数平面上の距離を求めよ.
慶應(医)過去問
投稿日:2023.02.25