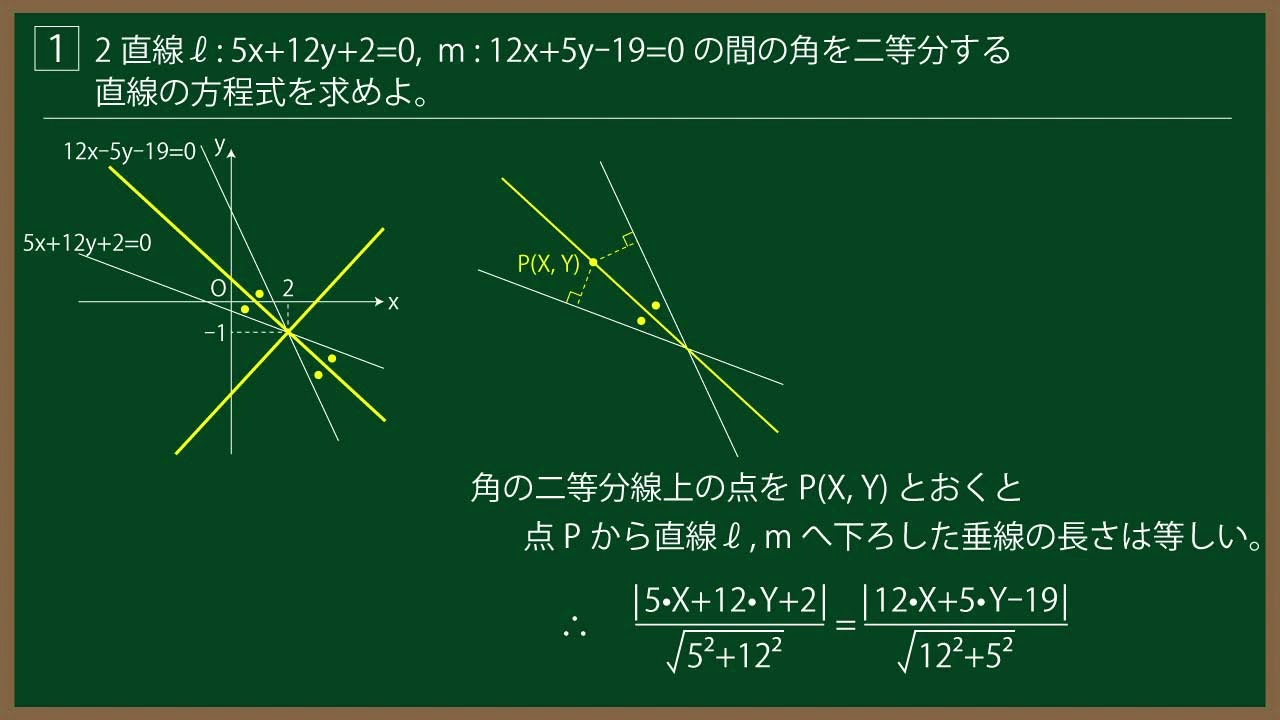
問題文全文(内容文):
岡山大学過去問題
(1)$x \leqq 0$において、常に$x^3+4x^2 \leqq ax+18$が成り立つaの範囲
(2)(1)で求めた範囲のaのうち最大のものを$a_0$
$x^3+4x^2 \leqq a_0x+18$を解け
岡山大学過去問題
(1)$x \leqq 0$において、常に$x^3+4x^2 \leqq ax+18$が成り立つaの範囲
(2)(1)で求めた範囲のaのうち最大のものを$a_0$
$x^3+4x^2 \leqq a_0x+18$を解け
単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#数学(高校生)#岡山大学
指導講師:
鈴木貫太郎
問題文全文(内容文):
岡山大学過去問題
(1)$x \leqq 0$において、常に$x^3+4x^2 \leqq ax+18$が成り立つaの範囲
(2)(1)で求めた範囲のaのうち最大のものを$a_0$
$x^3+4x^2 \leqq a_0x+18$を解け
岡山大学過去問題
(1)$x \leqq 0$において、常に$x^3+4x^2 \leqq ax+18$が成り立つaの範囲
(2)(1)で求めた範囲のaのうち最大のものを$a_0$
$x^3+4x^2 \leqq a_0x+18$を解け
投稿日:2018.07.17