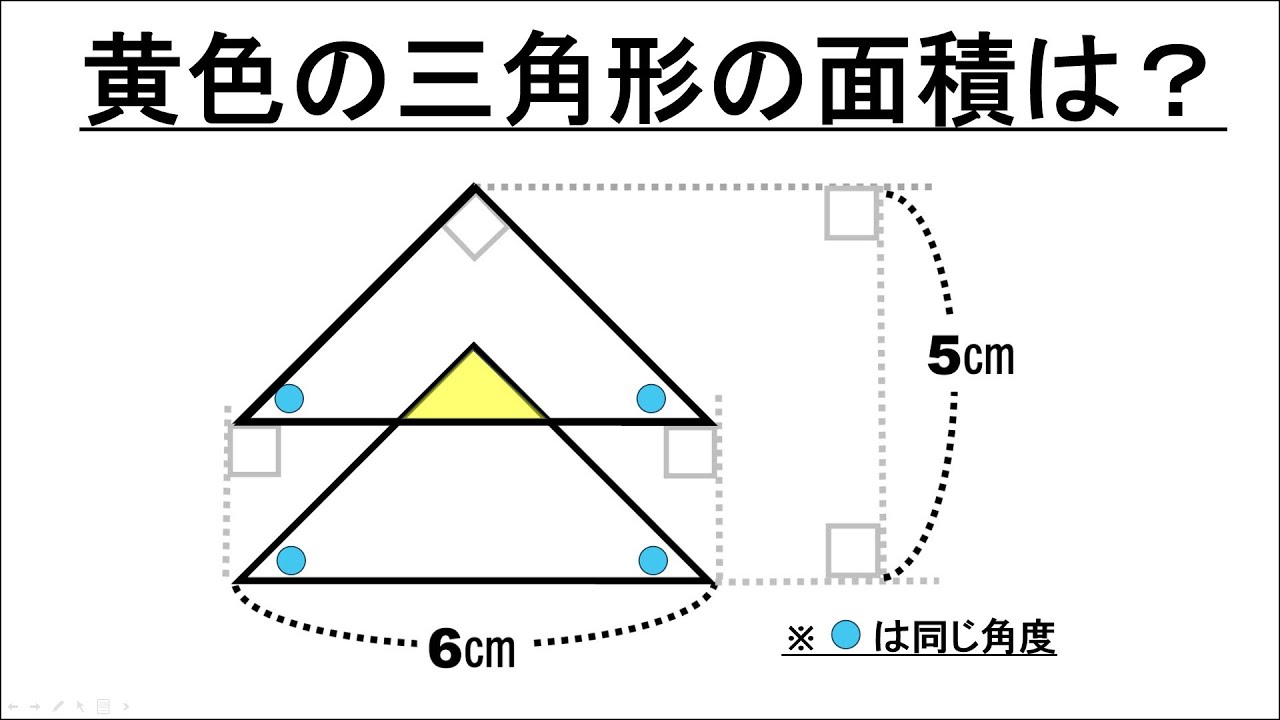
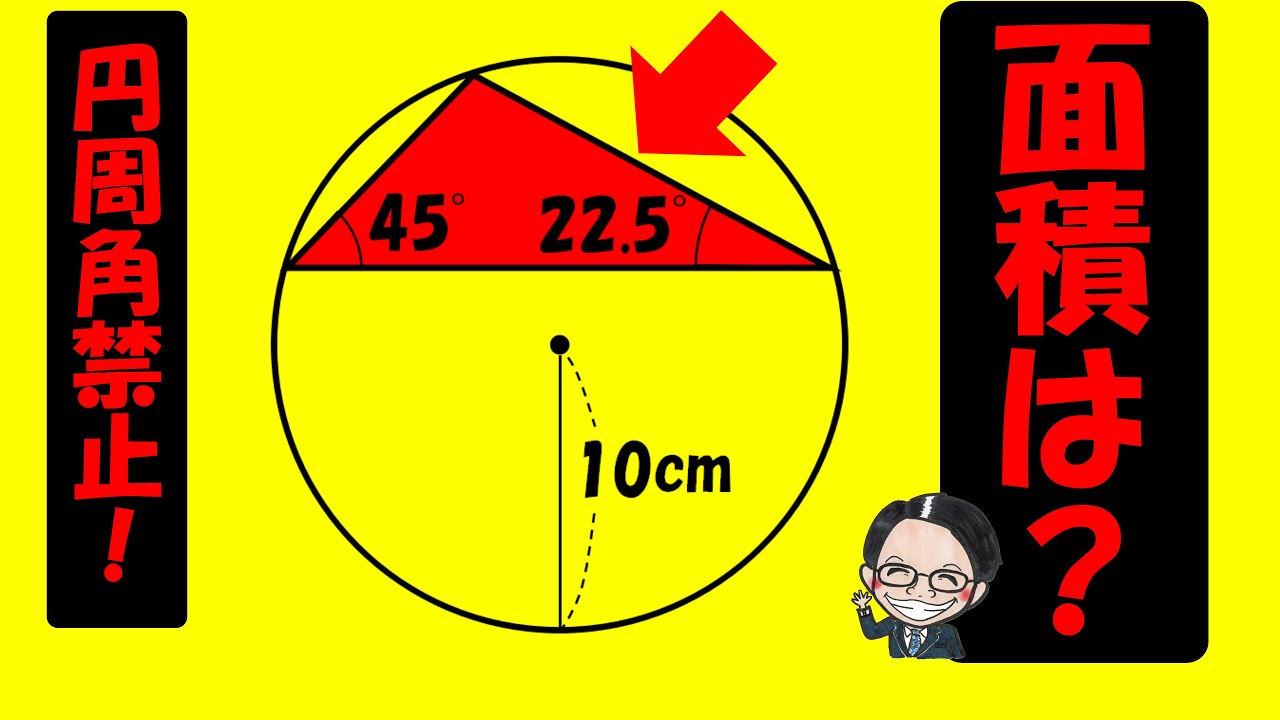
問題文全文(内容文):
右の図を、赤、青、黄、緑の4色でぬり分けることにします。
(1) 異なる3色を用いてぬり分ける方法は何通りありますか。
(2) 異なる2色を用いてぬり分ける方法は何通りありますか。
(3) ぬり分ける方法は全部で何通りありますか。
右の図を、赤、青、黄、緑の4色でぬり分けることにします。
(1) 異なる3色を用いてぬり分ける方法は何通りありますか。
(2) 異なる2色を用いてぬり分ける方法は何通りありますか。
(3) ぬり分ける方法は全部で何通りありますか。
チャプター:
0:00 オープニング
0:28 (1)
5:04 (2)
9:20 (3)
単元:
#算数(中学受験)#場合の数#場合の数
教材:
#SPX#5年算数D-支援#中学受験教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
右の図を、赤、青、黄、緑の4色でぬり分けることにします。
(1) 異なる3色を用いてぬり分ける方法は何通りありますか。
(2) 異なる2色を用いてぬり分ける方法は何通りありますか。
(3) ぬり分ける方法は全部で何通りありますか。
右の図を、赤、青、黄、緑の4色でぬり分けることにします。
(1) 異なる3色を用いてぬり分ける方法は何通りありますか。
(2) 異なる2色を用いてぬり分ける方法は何通りありますか。
(3) ぬり分ける方法は全部で何通りありますか。
投稿日:2025.08.22