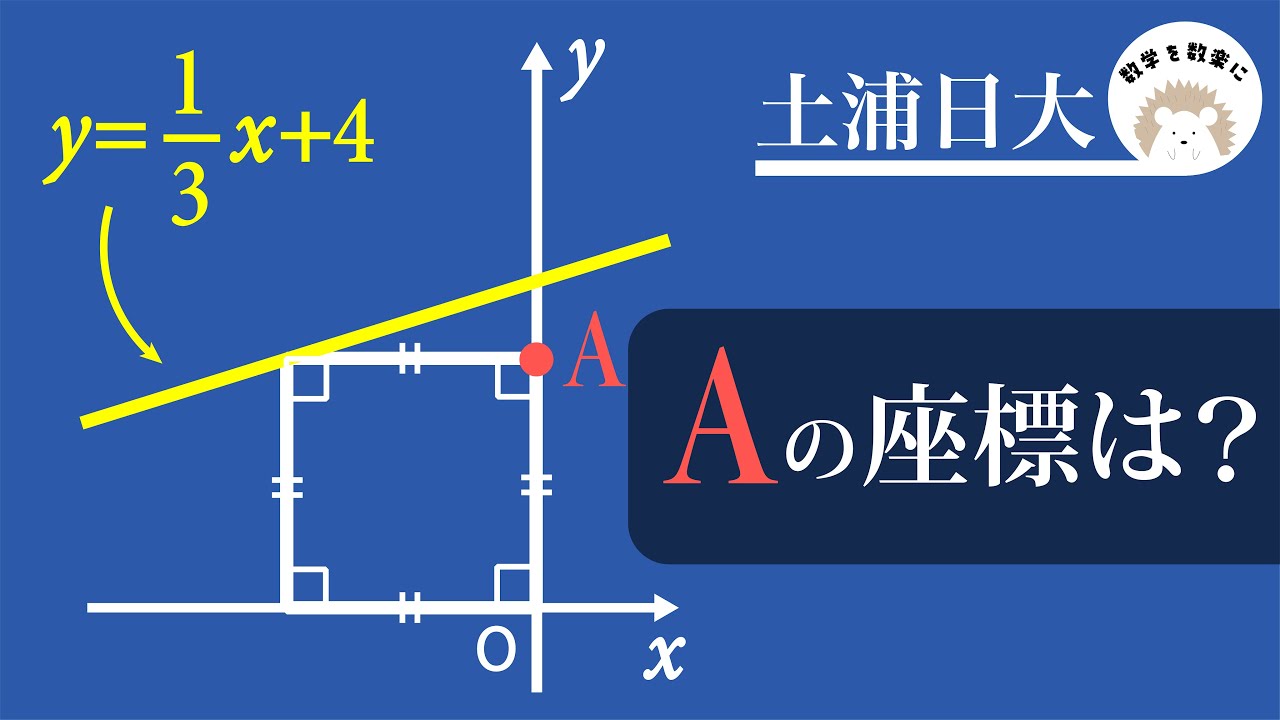
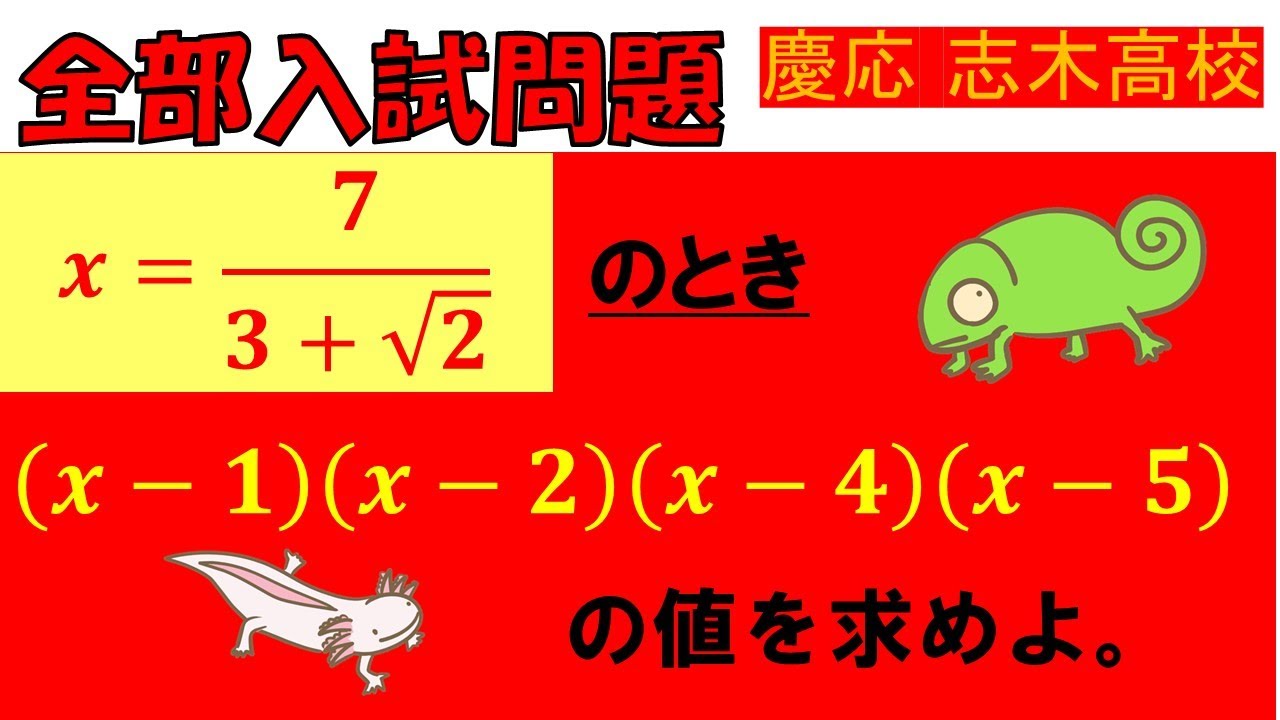
問題文全文(内容文):
高校受験対策・死守77
①$-3+(-2)$を計算しなさい。
➁$8-4÷(-2)^2$を計算しなさい。
③$5×(-5a)$を計算しなさい。
④$\frac{1}{2}x^2y÷\frac{1}{4}xy$を計算しなさい。
⑤$\sqrt{48}-\sqrt{3}$を計算しなさい。
⑥$(2a-b)^2$を展開しなさい。
⑦$x^2-x-42$を因数分解しなさい。
⑧半径が$6cm$で中心角が$45°$のおうぎ形の面積を求めなさい。
ただし、円周率は$\pi$とする。
⑨解が$-5,1$の2つの数となる、$x$についての2次方程式を1つ作りなさい。
⑩次のア~エのうち、数の集合と四則との関係について述べた文として正しいものをすべて選び、記号で答えなさい。
ア 自然数と自然数の加法の結果は、いつでも自然数となる。
イ 自然数と自然数の減法の結果は、いつでも整数となる。
ウ 自然数と自然数の乗法の結果は、いつでも自然数となる。
エ 自然数と自然数の除法の結果は、いつでも整数となる。
高校受験対策・死守77
①$-3+(-2)$を計算しなさい。
➁$8-4÷(-2)^2$を計算しなさい。
③$5×(-5a)$を計算しなさい。
④$\frac{1}{2}x^2y÷\frac{1}{4}xy$を計算しなさい。
⑤$\sqrt{48}-\sqrt{3}$を計算しなさい。
⑥$(2a-b)^2$を展開しなさい。
⑦$x^2-x-42$を因数分解しなさい。
⑧半径が$6cm$で中心角が$45°$のおうぎ形の面積を求めなさい。
ただし、円周率は$\pi$とする。
⑨解が$-5,1$の2つの数となる、$x$についての2次方程式を1つ作りなさい。
⑩次のア~エのうち、数の集合と四則との関係について述べた文として正しいものをすべて選び、記号で答えなさい。
ア 自然数と自然数の加法の結果は、いつでも自然数となる。
イ 自然数と自然数の減法の結果は、いつでも整数となる。
ウ 自然数と自然数の乗法の結果は、いつでも自然数となる。
エ 自然数と自然数の除法の結果は、いつでも整数となる。
単元:
#数学(中学生)#中1数学#中2数学#中3数学#正の数・負の数#方程式#式の計算(単項式・多項式・式の四則計算)#連立方程式#式の計算(展開、因数分解)#平方根#2次方程式#1次関数#文字と式#平面図形
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
高校受験対策・死守77
①$-3+(-2)$を計算しなさい。
➁$8-4÷(-2)^2$を計算しなさい。
③$5×(-5a)$を計算しなさい。
④$\frac{1}{2}x^2y÷\frac{1}{4}xy$を計算しなさい。
⑤$\sqrt{48}-\sqrt{3}$を計算しなさい。
⑥$(2a-b)^2$を展開しなさい。
⑦$x^2-x-42$を因数分解しなさい。
⑧半径が$6cm$で中心角が$45°$のおうぎ形の面積を求めなさい。
ただし、円周率は$\pi$とする。
⑨解が$-5,1$の2つの数となる、$x$についての2次方程式を1つ作りなさい。
⑩次のア~エのうち、数の集合と四則との関係について述べた文として正しいものをすべて選び、記号で答えなさい。
ア 自然数と自然数の加法の結果は、いつでも自然数となる。
イ 自然数と自然数の減法の結果は、いつでも整数となる。
ウ 自然数と自然数の乗法の結果は、いつでも自然数となる。
エ 自然数と自然数の除法の結果は、いつでも整数となる。
高校受験対策・死守77
①$-3+(-2)$を計算しなさい。
➁$8-4÷(-2)^2$を計算しなさい。
③$5×(-5a)$を計算しなさい。
④$\frac{1}{2}x^2y÷\frac{1}{4}xy$を計算しなさい。
⑤$\sqrt{48}-\sqrt{3}$を計算しなさい。
⑥$(2a-b)^2$を展開しなさい。
⑦$x^2-x-42$を因数分解しなさい。
⑧半径が$6cm$で中心角が$45°$のおうぎ形の面積を求めなさい。
ただし、円周率は$\pi$とする。
⑨解が$-5,1$の2つの数となる、$x$についての2次方程式を1つ作りなさい。
⑩次のア~エのうち、数の集合と四則との関係について述べた文として正しいものをすべて選び、記号で答えなさい。
ア 自然数と自然数の加法の結果は、いつでも自然数となる。
イ 自然数と自然数の減法の結果は、いつでも整数となる。
ウ 自然数と自然数の乗法の結果は、いつでも自然数となる。
エ 自然数と自然数の除法の結果は、いつでも整数となる。
投稿日:2021.10.09