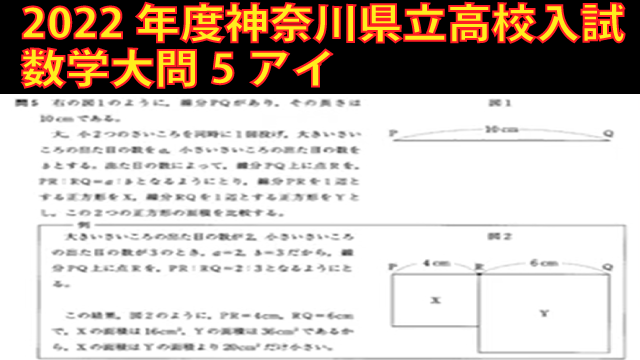
問題文全文(内容文):
問4 右の図において、直線①は関数$y=x+3$のグラフであり、曲線②は関数$y=ax^2$のグラフである。 点Aは直線①と曲線②との交点で、そのx座標は6である。点Bは曲線②状の点で、線分ABはx軸に平行である。点Cは直線①上の点で、線分BCはy軸に平行である。
また、点Dは線分BCとx軸との交点である。
さらに、減点をOとするとき、点Eはx軸上の点で、$DO:OE=6:5$であり、そのx座標は正である。このとき、次の問いに答えなさい。
(ア)曲線②の式y=ax²のaの値として正しいものを次の1~6の中から1つ選び、その番号を答えなさい。
1.$a=\dfrac{1}{6}$ 2.$a=\dfrac{1}{4}$ 3.$a=\dfrac{1}{3}$ 4.$a=\dfrac{1}{2}$ 5.$a=\dfrac{3}{4}$ 6.$a=\dfrac{3}{2}$
(イ)直線CEの式をy=mx+nとするとき、(ⅰ)mの値と、(ⅱ)nの値として正しいものを、それぞれ次の1~6の中から1つずつ選び、その番号を答えなさい。
(ⅰ)mの値
1.$m=\dfrac{3}{13}$ 2.$m=\dfrac{1}{4}$ 3.$m=\dfrac{3}{11}$ 4.$m=\dfrac{3}{10}$ 5.$m=\dfrac{1}{3}$ 6.$m=\dfrac{3}{8}$
(ⅱ)nの値
1.$n=\dfrac{-17}{11}$ 2.$n=\dfrac{-20}{13}$ 3.$n=\dfrac{-3}{2}$
4.$n=\dfrac{-18}{13}$ 5.$n=\dfrac{-15}{11}$ 6.$n=\dfrac{-11}{10}$
問4 右の図において、直線①は関数$y=x+3$のグラフであり、曲線②は関数$y=ax^2$のグラフである。 点Aは直線①と曲線②との交点で、そのx座標は6である。点Bは曲線②状の点で、線分ABはx軸に平行である。点Cは直線①上の点で、線分BCはy軸に平行である。
また、点Dは線分BCとx軸との交点である。
さらに、減点をOとするとき、点Eはx軸上の点で、$DO:OE=6:5$であり、そのx座標は正である。このとき、次の問いに答えなさい。
(ア)曲線②の式y=ax²のaの値として正しいものを次の1~6の中から1つ選び、その番号を答えなさい。
1.$a=\dfrac{1}{6}$ 2.$a=\dfrac{1}{4}$ 3.$a=\dfrac{1}{3}$ 4.$a=\dfrac{1}{2}$ 5.$a=\dfrac{3}{4}$ 6.$a=\dfrac{3}{2}$
(イ)直線CEの式をy=mx+nとするとき、(ⅰ)mの値と、(ⅱ)nの値として正しいものを、それぞれ次の1~6の中から1つずつ選び、その番号を答えなさい。
(ⅰ)mの値
1.$m=\dfrac{3}{13}$ 2.$m=\dfrac{1}{4}$ 3.$m=\dfrac{3}{11}$ 4.$m=\dfrac{3}{10}$ 5.$m=\dfrac{1}{3}$ 6.$m=\dfrac{3}{8}$
(ⅱ)nの値
1.$n=\dfrac{-17}{11}$ 2.$n=\dfrac{-20}{13}$ 3.$n=\dfrac{-3}{2}$
4.$n=\dfrac{-18}{13}$ 5.$n=\dfrac{-15}{11}$ 6.$n=\dfrac{-11}{10}$
チャプター:
00:00 オープニング
00:05 (ア)の解説
01:07 (イ)の解説
04:10 エンディング
単元:
#数学(中学生)#高校入試過去問(数学)#神奈川県公立高校入試
指導講師:
理数個別チャンネル
問題文全文(内容文):
問4 右の図において、直線①は関数$y=x+3$のグラフであり、曲線②は関数$y=ax^2$のグラフである。 点Aは直線①と曲線②との交点で、そのx座標は6である。点Bは曲線②状の点で、線分ABはx軸に平行である。点Cは直線①上の点で、線分BCはy軸に平行である。
また、点Dは線分BCとx軸との交点である。
さらに、減点をOとするとき、点Eはx軸上の点で、$DO:OE=6:5$であり、そのx座標は正である。このとき、次の問いに答えなさい。
(ア)曲線②の式y=ax²のaの値として正しいものを次の1~6の中から1つ選び、その番号を答えなさい。
1.$a=\dfrac{1}{6}$ 2.$a=\dfrac{1}{4}$ 3.$a=\dfrac{1}{3}$ 4.$a=\dfrac{1}{2}$ 5.$a=\dfrac{3}{4}$ 6.$a=\dfrac{3}{2}$
(イ)直線CEの式をy=mx+nとするとき、(ⅰ)mの値と、(ⅱ)nの値として正しいものを、それぞれ次の1~6の中から1つずつ選び、その番号を答えなさい。
(ⅰ)mの値
1.$m=\dfrac{3}{13}$ 2.$m=\dfrac{1}{4}$ 3.$m=\dfrac{3}{11}$ 4.$m=\dfrac{3}{10}$ 5.$m=\dfrac{1}{3}$ 6.$m=\dfrac{3}{8}$
(ⅱ)nの値
1.$n=\dfrac{-17}{11}$ 2.$n=\dfrac{-20}{13}$ 3.$n=\dfrac{-3}{2}$
4.$n=\dfrac{-18}{13}$ 5.$n=\dfrac{-15}{11}$ 6.$n=\dfrac{-11}{10}$
問4 右の図において、直線①は関数$y=x+3$のグラフであり、曲線②は関数$y=ax^2$のグラフである。 点Aは直線①と曲線②との交点で、そのx座標は6である。点Bは曲線②状の点で、線分ABはx軸に平行である。点Cは直線①上の点で、線分BCはy軸に平行である。
また、点Dは線分BCとx軸との交点である。
さらに、減点をOとするとき、点Eはx軸上の点で、$DO:OE=6:5$であり、そのx座標は正である。このとき、次の問いに答えなさい。
(ア)曲線②の式y=ax²のaの値として正しいものを次の1~6の中から1つ選び、その番号を答えなさい。
1.$a=\dfrac{1}{6}$ 2.$a=\dfrac{1}{4}$ 3.$a=\dfrac{1}{3}$ 4.$a=\dfrac{1}{2}$ 5.$a=\dfrac{3}{4}$ 6.$a=\dfrac{3}{2}$
(イ)直線CEの式をy=mx+nとするとき、(ⅰ)mの値と、(ⅱ)nの値として正しいものを、それぞれ次の1~6の中から1つずつ選び、その番号を答えなさい。
(ⅰ)mの値
1.$m=\dfrac{3}{13}$ 2.$m=\dfrac{1}{4}$ 3.$m=\dfrac{3}{11}$ 4.$m=\dfrac{3}{10}$ 5.$m=\dfrac{1}{3}$ 6.$m=\dfrac{3}{8}$
(ⅱ)nの値
1.$n=\dfrac{-17}{11}$ 2.$n=\dfrac{-20}{13}$ 3.$n=\dfrac{-3}{2}$
4.$n=\dfrac{-18}{13}$ 5.$n=\dfrac{-15}{11}$ 6.$n=\dfrac{-11}{10}$
投稿日:2022.06.29