【高校数学】同じものを含む順列～考え方は簡単～1-11 【数学A】 - 質問解決D.B.（データベース）
Generic selectors
完全一致検索
タイトルから検索
記事本文から検索
Post Type Selectors
all_unit_post
質問解決D.B.（データベース） > 動画投稿 > 数学(高校生) > 数A > 場合の数と確率 > 場合の数 > 【高校数学】同じものを含む順列～考え方は簡単～1-11 【数学A】

【高校数学】同じものを含む順列～考え方は簡単～1-11 【数学A】

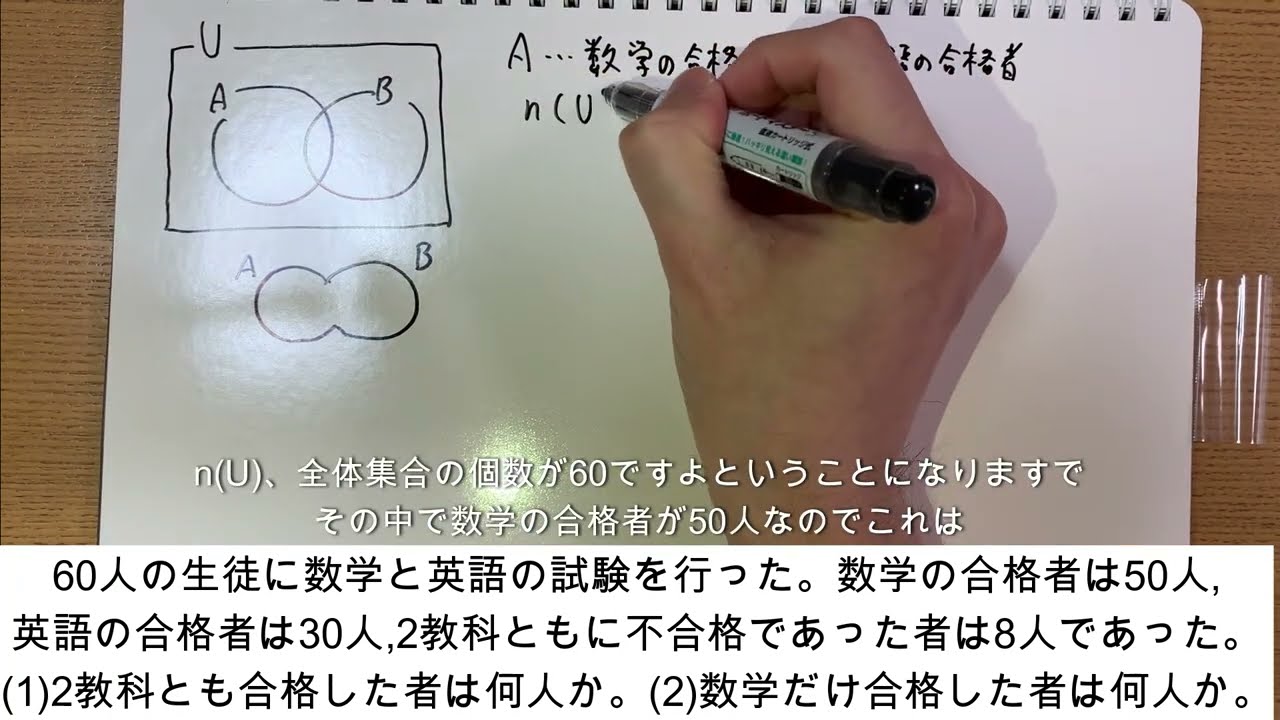
問題文全文(内容文)：
同じものを含む順列解説動画です
チャプター：

00:00 はじまり

00:27 同じものを含む順列とは

01:24 一つ目の解き方

03:33 もう一つの解き方

04:29 解き方の整理

04:59 真面目な説明

06:15 例題一問

08:14 まとめ

08:43 まとめノート

単元： #数A#場合の数と確率#場合の数#数学(高校生)
指導講師： 【楽しい授業動画】あきとんとん
問題文全文(内容文)：
同じものを含む順列解説動画です
投稿日：2020.06.23

＜関連動画＞

【高校数学】　　数A－１９　　確率①　・　さいころ編Part.1

アイキャッチ画像
単元： #数A#場合の数と確率#確率#数学(高校生)
指導講師： とある男が授業をしてみた
問題文全文(内容文)：
◎3個のさいころを同時に投げるとき、次の場合の確率は？

①目の和が6になる。
②少なくとも1個は3の目が出る。
③目の積が5の倍数になる。
④少なくとも2個の目が同じである。
この動画を見る　

福田の数学〜立教大学2025理学部第1問(4)〜確率の基本的な性質

アイキャッチ画像
単元： #数A#大学入試過去問(数学)#場合の数と確率#確率#学校別大学入試過去問解説(数学)#立教大学#数学(高校生)
指導講師： 福田次郎
問題文全文(内容文)：

$\boxed{1}$

(4)箱の中に緑色のカードが$5$枚、

黄色のカードが$4$枚、赤色のカードが$3$枚

入っている。

箱から無作為にカードを$3$枚取り出すとき、

$3$枚とも同じ色である確率は$\boxed{オ}$、

$3$枚の色がすべて異なる確率は$\boxed{カ}$、

$2$枚が同じ色であり、かつ、

残りの$1$枚が他の$2$枚と異なる色である確率は

$\boxed{キ}$である。

$2025$年立教大学理学部過去問題
この動画を見る　

福田の1.5倍速演習〜合格する重要問題043〜北海道大学2017年度文系第３問〜確率漸化式の定番問題

アイキャッチ画像
単元： #数A#大学入試過去問(数学)#場合の数と確率#確率#数列#漸化式#学校別大学入試過去問解説(数学)#数学(高校生)#北海道大学#数B
指導講師： 福田次郎
問題文全文(内容文)：
正四面体ABCDの頂点を移動する点Pがある。点Pは、1秒ごとに、
隣の3頂点のいずれかに等しい確率$\frac{a}{3}$で移るか、もとの頂点に確率1-aで
留まる。初め頂点Aにいた点Pが、n秒後に頂点Aにいる確率を$p_n$とする。
ただし、$0 \lt a \lt 1$とし、nは自然数とする。

(1)数列$\left\{p_n\right\}$の漸化式を求めよ。
(2)確率$p_n$を求めよ。

2017北海道大学文系過去問
この動画を見る　

福田の一夜漬け数学〜順列・組合せ(4)〜円順列（前編）

アイキャッチ画像
単元： #数A#場合の数と確率#場合の数#数学(高校生)
指導講師： 福田次郎
問題文全文(内容文)：
${\Large\boxed{1}}$　8人が円形のテーブルに座るとき
(1)特定の2人が隣り合う並び方は何通りか。
(2)特定の2人が向かい合う並び方は何通りか。

${\Large\boxed{2}}$　8人が次のようなテーブルに座る方法は何通りか。
(1)正方形のテーブル。各辺に2人ずつ座る。
(2)長方形のテーブル。長辺に3人、短辺に1人座る。

${\Large\boxed{3}}$　立方体の6面に色を塗る。隣り合う面には違う色を塗る。
(1)6色で塗り分ける方法は何通りあるか。
(2)5色で塗り分ける方法は何通りあるか。
この動画を見る　

【高校数学】集合と部分集合～記号の意味を理解しようぜ～ 1-1【数学A 】

アイキャッチ画像
単元： #数Ⅰ#数A#数と式#場合の数と確率#集合と命題（集合・命題と条件・背理法）#場合の数#数学(高校生)
指導講師： 【楽しい授業動画】あきとんとん
問題文全文(内容文)：
集合と部分集合説明動画です
この動画を見る　
PAGE TOP