問題文全文(内容文):
例1
下の図の四角形$ABCD$で,辺$BC$を$C$の方に延長した直線上に点$E$をとり,
四角形$ABCD$と面積が等しい$\triangle ABC$を書きなさい.
例2
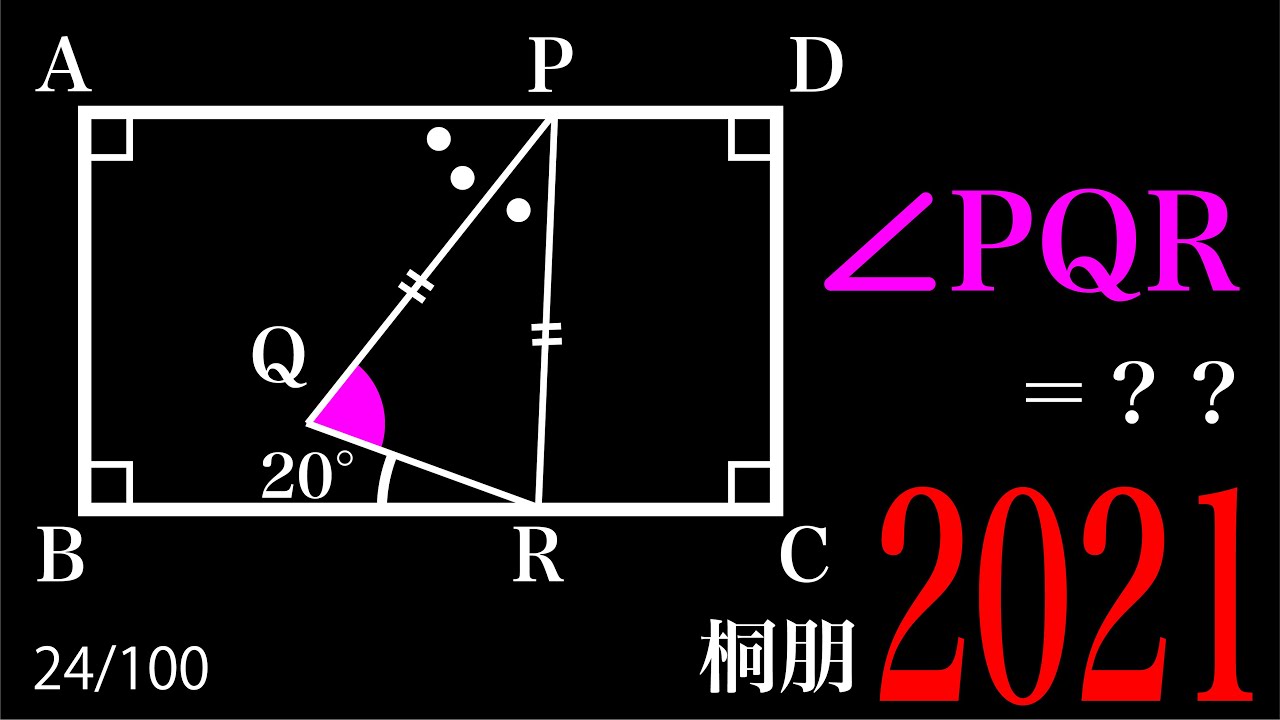
下の図のように,折れ線$PQR$を境界とする2つの土地があります.
それぞれの土地の面積を考えないで,境界を点$P$を通る線分にあらためるとき,
点$P$を通る線分を書きなさい.
例1
下の図の四角形$ABCD$で,辺$BC$を$C$の方に延長した直線上に点$E$をとり,
四角形$ABCD$と面積が等しい$\triangle ABC$を書きなさい.
例2
下の図のように,折れ線$PQR$を境界とする2つの土地があります.
それぞれの土地の面積を考えないで,境界を点$P$を通る線分にあらためるとき,
点$P$を通る線分を書きなさい.
単元:
#数学(中学生)#中2数学#三角形と四角形
指導講師:
中学受験算数・高校受験数学けいたくチャンネル
問題文全文(内容文):
例1
下の図の四角形$ABCD$で,辺$BC$を$C$の方に延長した直線上に点$E$をとり,
四角形$ABCD$と面積が等しい$\triangle ABC$を書きなさい.
例2
下の図のように,折れ線$PQR$を境界とする2つの土地があります.
それぞれの土地の面積を考えないで,境界を点$P$を通る線分にあらためるとき,
点$P$を通る線分を書きなさい.
例1
下の図の四角形$ABCD$で,辺$BC$を$C$の方に延長した直線上に点$E$をとり,
四角形$ABCD$と面積が等しい$\triangle ABC$を書きなさい.
例2
下の図のように,折れ線$PQR$を境界とする2つの土地があります.
それぞれの土地の面積を考えないで,境界を点$P$を通る線分にあらためるとき,
点$P$を通る線分を書きなさい.
投稿日:2023.04.24