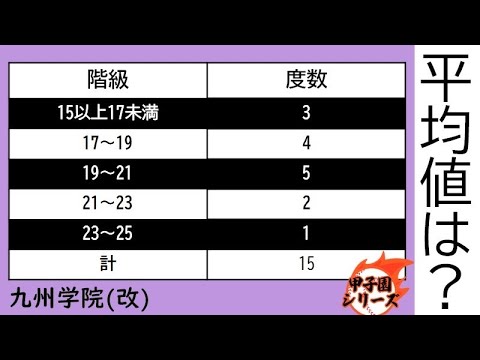
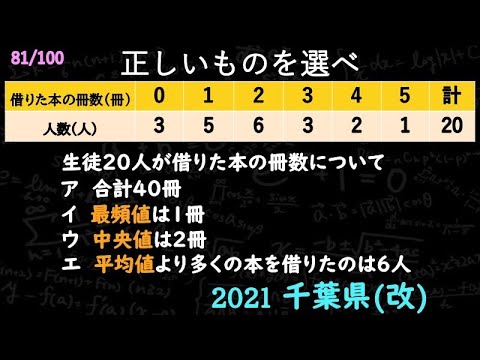
問題文全文(内容文):
$\Large\boxed{5}$ 下図(※動画参照)は、あるクラスの40人の生徒の数学と理科の試験得点の散布図である。
データ点の近くの数値はそのデータ点の生徒の出席番号である。
(1)数学と理科の合計得点が最も高い生徒の出席番号は$\boxed{\ \ ヒ\ \ }$である。また、数学と理科の得点差の絶対値が最も大きい生徒の出席番号は$\boxed{\ \ フ\ \ }$である。
(2)数学と理科それぞれの得点の平均値を$\bar{x}$, $\bar{y}$、標準偏差を$s_x$, $s_y$、数学と理科の得点の共分散を$s_{xy}$と表すと、これらの数値は以下であった。
$\bar{x}$=67.7, $\bar{y}$=70.9, $s_x$=14.9, $s_y$=11.5, $s_{xy}$=115.7
数学の得点と理科の得点の相関係数は$\boxed{\ \ ヘ\ \ }$である。なお、答えは小数第3位を四捨五入し、小数第2位まで求めなさい。
(3)各生徒の数学の得点を$x_1$, $x_2$, ..., $x_{40}$、理科の得点を$y_1$, $y_2$, ..., $y_{40}$で表す。
数学と理科の合計得点$x_1$+$y_1$, $x_2$+$y_2$, ..., $x_{40}$+$y_{40}$の平均値は$\bar{x}$, $\bar{y}$を用いると$\boxed{\ \ ホ\ \ }$と表せる。合計得点の分散は、
$\displaystyle\frac{1}{40}\sum_{i=1}^{40}\left(x_i+y_i-\boxed{\ ホ\ }\right)^2$
であるから、これを式変形すると、合計得点の分散は、$s_x$, $s_y$, $s_{xy}$を用いて$\boxed{\ \ マ\ \ }$と表せる。これらの式に(2)で与えられた数値を入れて計算すると、数学と理科の合計得点の平均値は$\boxed{\ \ ミ\ \ }$、分散は$\boxed{\ \ ム\ \ }$である。なお、答えは小数第2位を四捨五入し、小数第1位まで求めなさい。
$\Large\boxed{5}$ 下図(※動画参照)は、あるクラスの40人の生徒の数学と理科の試験得点の散布図である。
データ点の近くの数値はそのデータ点の生徒の出席番号である。
(1)数学と理科の合計得点が最も高い生徒の出席番号は$\boxed{\ \ ヒ\ \ }$である。また、数学と理科の得点差の絶対値が最も大きい生徒の出席番号は$\boxed{\ \ フ\ \ }$である。
(2)数学と理科それぞれの得点の平均値を$\bar{x}$, $\bar{y}$、標準偏差を$s_x$, $s_y$、数学と理科の得点の共分散を$s_{xy}$と表すと、これらの数値は以下であった。
$\bar{x}$=67.7, $\bar{y}$=70.9, $s_x$=14.9, $s_y$=11.5, $s_{xy}$=115.7
数学の得点と理科の得点の相関係数は$\boxed{\ \ ヘ\ \ }$である。なお、答えは小数第3位を四捨五入し、小数第2位まで求めなさい。
(3)各生徒の数学の得点を$x_1$, $x_2$, ..., $x_{40}$、理科の得点を$y_1$, $y_2$, ..., $y_{40}$で表す。
数学と理科の合計得点$x_1$+$y_1$, $x_2$+$y_2$, ..., $x_{40}$+$y_{40}$の平均値は$\bar{x}$, $\bar{y}$を用いると$\boxed{\ \ ホ\ \ }$と表せる。合計得点の分散は、
$\displaystyle\frac{1}{40}\sum_{i=1}^{40}\left(x_i+y_i-\boxed{\ ホ\ }\right)^2$
であるから、これを式変形すると、合計得点の分散は、$s_x$, $s_y$, $s_{xy}$を用いて$\boxed{\ \ マ\ \ }$と表せる。これらの式に(2)で与えられた数値を入れて計算すると、数学と理科の合計得点の平均値は$\boxed{\ \ ミ\ \ }$、分散は$\boxed{\ \ ム\ \ }$である。なお、答えは小数第2位を四捨五入し、小数第1位まで求めなさい。
単元:
#データの分析#データの分析#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{5}$ 下図(※動画参照)は、あるクラスの40人の生徒の数学と理科の試験得点の散布図である。
データ点の近くの数値はそのデータ点の生徒の出席番号である。
(1)数学と理科の合計得点が最も高い生徒の出席番号は$\boxed{\ \ ヒ\ \ }$である。また、数学と理科の得点差の絶対値が最も大きい生徒の出席番号は$\boxed{\ \ フ\ \ }$である。
(2)数学と理科それぞれの得点の平均値を$\bar{x}$, $\bar{y}$、標準偏差を$s_x$, $s_y$、数学と理科の得点の共分散を$s_{xy}$と表すと、これらの数値は以下であった。
$\bar{x}$=67.7, $\bar{y}$=70.9, $s_x$=14.9, $s_y$=11.5, $s_{xy}$=115.7
数学の得点と理科の得点の相関係数は$\boxed{\ \ ヘ\ \ }$である。なお、答えは小数第3位を四捨五入し、小数第2位まで求めなさい。
(3)各生徒の数学の得点を$x_1$, $x_2$, ..., $x_{40}$、理科の得点を$y_1$, $y_2$, ..., $y_{40}$で表す。
数学と理科の合計得点$x_1$+$y_1$, $x_2$+$y_2$, ..., $x_{40}$+$y_{40}$の平均値は$\bar{x}$, $\bar{y}$を用いると$\boxed{\ \ ホ\ \ }$と表せる。合計得点の分散は、
$\displaystyle\frac{1}{40}\sum_{i=1}^{40}\left(x_i+y_i-\boxed{\ ホ\ }\right)^2$
であるから、これを式変形すると、合計得点の分散は、$s_x$, $s_y$, $s_{xy}$を用いて$\boxed{\ \ マ\ \ }$と表せる。これらの式に(2)で与えられた数値を入れて計算すると、数学と理科の合計得点の平均値は$\boxed{\ \ ミ\ \ }$、分散は$\boxed{\ \ ム\ \ }$である。なお、答えは小数第2位を四捨五入し、小数第1位まで求めなさい。
$\Large\boxed{5}$ 下図(※動画参照)は、あるクラスの40人の生徒の数学と理科の試験得点の散布図である。
データ点の近くの数値はそのデータ点の生徒の出席番号である。
(1)数学と理科の合計得点が最も高い生徒の出席番号は$\boxed{\ \ ヒ\ \ }$である。また、数学と理科の得点差の絶対値が最も大きい生徒の出席番号は$\boxed{\ \ フ\ \ }$である。
(2)数学と理科それぞれの得点の平均値を$\bar{x}$, $\bar{y}$、標準偏差を$s_x$, $s_y$、数学と理科の得点の共分散を$s_{xy}$と表すと、これらの数値は以下であった。
$\bar{x}$=67.7, $\bar{y}$=70.9, $s_x$=14.9, $s_y$=11.5, $s_{xy}$=115.7
数学の得点と理科の得点の相関係数は$\boxed{\ \ ヘ\ \ }$である。なお、答えは小数第3位を四捨五入し、小数第2位まで求めなさい。
(3)各生徒の数学の得点を$x_1$, $x_2$, ..., $x_{40}$、理科の得点を$y_1$, $y_2$, ..., $y_{40}$で表す。
数学と理科の合計得点$x_1$+$y_1$, $x_2$+$y_2$, ..., $x_{40}$+$y_{40}$の平均値は$\bar{x}$, $\bar{y}$を用いると$\boxed{\ \ ホ\ \ }$と表せる。合計得点の分散は、
$\displaystyle\frac{1}{40}\sum_{i=1}^{40}\left(x_i+y_i-\boxed{\ ホ\ }\right)^2$
であるから、これを式変形すると、合計得点の分散は、$s_x$, $s_y$, $s_{xy}$を用いて$\boxed{\ \ マ\ \ }$と表せる。これらの式に(2)で与えられた数値を入れて計算すると、数学と理科の合計得点の平均値は$\boxed{\ \ ミ\ \ }$、分散は$\boxed{\ \ ム\ \ }$である。なお、答えは小数第2位を四捨五入し、小数第1位まで求めなさい。
投稿日:2024.04.07