 データの分析
データの分析
 データの分析
データの分析
データの分析 4S数学問題集数Ⅰ 332 ヒストグラムと箱ひげ図1【ユースケ・マセマティックがていねいに解説】
単元:
#数Ⅰ#データの分析#データの分析#数学(高校生)
教材:
#4S数学#4S数学Ⅰ+AのB問題解説(新課程2022年以降)#データの分析#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
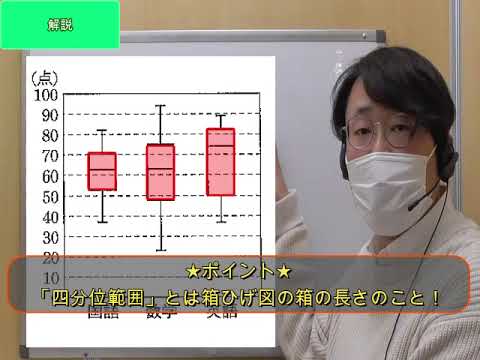
右の図は、400人の生徒が受験した国語、数学、英語のテストの得点のデータの箱ひげ図である。この箱ひげ図から読み取れることとして正しいものを、次の①~⑤からすべて選べ。
① 範囲が最も大きいのは英語である。
② 四分位範囲が最も小さいのは国語である。
③ 60点以上の生徒は、国語と数学では200人以上、英語では300人以上いる。
④ 50点未満の生徒は、国語と英語では100人以下、数学では100人以上いる。
⑤ 30点台の生徒は、国語と英語ではいるが、数学ではいない。
※箱ひげ図は動画内に載せております。
この動画を見る
右の図は、400人の生徒が受験した国語、数学、英語のテストの得点のデータの箱ひげ図である。この箱ひげ図から読み取れることとして正しいものを、次の①~⑤からすべて選べ。
① 範囲が最も大きいのは英語である。
② 四分位範囲が最も小さいのは国語である。
③ 60点以上の生徒は、国語と数学では200人以上、英語では300人以上いる。
④ 50点未満の生徒は、国語と英語では100人以下、数学では100人以上いる。
⑤ 30点台の生徒は、国語と英語ではいるが、数学ではいない。
※箱ひげ図は動画内に載せております。
データの分析 4S数学問題集数Ⅰ 356 仮説検定2 【ユースケ・マセマティックがていねいに解説】

単元:
#数Ⅰ#データの分析#データの分析#数学(高校生)
教材:
#4S数学#4S数学Ⅰ+AのB問題解説(新課程2022年以降)#データの分析#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
(1)1枚の公正なコインを10回投げるとき、すべて表が出る確率を反復試行の確率の公式を用いて求めよ。また、表がちょうど9回出る確率を求めよ。
(2)1枚のコインを10回投げたところ、表が9回出た。このコインは表が出やすいと判断して良いか。仮説検定の考え方を用い、基準となる確率を0.05として考察せよ。ただし(1)の結果を用いよ。
この動画を見る
(1)1枚の公正なコインを10回投げるとき、すべて表が出る確率を反復試行の確率の公式を用いて求めよ。また、表がちょうど9回出る確率を求めよ。
(2)1枚のコインを10回投げたところ、表が9回出た。このコインは表が出やすいと判断して良いか。仮説検定の考え方を用い、基準となる確率を0.05として考察せよ。ただし(1)の結果を用いよ。
データの分析 4S数学問題集数Ⅰ 355 仮説検定1 【ユースケ・マセマティックがていねいに解説】

単元:
#数Ⅰ#データの分析#データの分析#数学(高校生)
教材:
#4S数学#4S数学Ⅰ+AのB問題解説(新課程2022年以降)#データの分析#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
以前、ある芸能人を知っているか街頭で大規模なアンケートをとったところ、全体の1/8の人が知っていると答えた。その1年後、再び同じ芸能人について、100人の人にアンケートをとったところ、19人が知っていると答えた。この時、この芸能人の知名度は上がったと判断して良いか。仮説検定の考え方を用い、次の(1)、(2)の場合において考察せよ。ただし、公正な8面さいころを100回投げて1の目が出た回数を記録する実験を800セット行ったところ次の表のようになったとし、この結果を用いよ。
1の目が出た回数 4 5 6 7 8 9 10 11 12 13
度数 2 9 8 24 32 65 71 83 107 94
1の目が出た回数 14 15 16 17 18 19 20 21 22 23
合計度数 88 69 54 42 25 11 7 5 3 1 800
(1) 基準となる確率 0.05
(2) 基準となる確率 0.01
この動画を見る
以前、ある芸能人を知っているか街頭で大規模なアンケートをとったところ、全体の1/8の人が知っていると答えた。その1年後、再び同じ芸能人について、100人の人にアンケートをとったところ、19人が知っていると答えた。この時、この芸能人の知名度は上がったと判断して良いか。仮説検定の考え方を用い、次の(1)、(2)の場合において考察せよ。ただし、公正な8面さいころを100回投げて1の目が出た回数を記録する実験を800セット行ったところ次の表のようになったとし、この結果を用いよ。
1の目が出た回数 4 5 6 7 8 9 10 11 12 13
度数 2 9 8 24 32 65 71 83 107 94
1の目が出た回数 14 15 16 17 18 19 20 21 22 23
合計度数 88 69 54 42 25 11 7 5 3 1 800
(1) 基準となる確率 0.05
(2) 基準となる確率 0.01
データの分析 4S数学問題集数Ⅰ 349 相関係数2 【ユースケ・マセマティックがていねいに解説】

単元:
#数Ⅰ#データの分析#データの分析#数学(高校生)
教材:
#4S数学#4S数学Ⅰ+AのB問題解説(新課程2022年以降)#データの分析#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
下の表は10人の生徒の右手と左手の握力を測定した結果である。
右手と左手の握力の相関係数を求めよ。ただし、小数第3位を四捨五入せよ。
生徒の番号 1 2 3 4 5 6 7 8 9 10
右手の握力(kg) 36 42 35 33 38 32 39 40 34 41
左手の握力(kg) 27 39 35 25 41 23 43 31 29 37
この動画を見る
下の表は10人の生徒の右手と左手の握力を測定した結果である。
右手と左手の握力の相関係数を求めよ。ただし、小数第3位を四捨五入せよ。
生徒の番号 1 2 3 4 5 6 7 8 9 10
右手の握力(kg) 36 42 35 33 38 32 39 40 34 41
左手の握力(kg) 27 39 35 25 41 23 43 31 29 37
データの分析 4S数学問題集数Ⅰ 348 相関係数1 【ユースケ・マセマティックがていねいに解説】

単元:
#数Ⅰ#データの分析#データの分析#数学(高校生)
教材:
#4S数学#4S数学Ⅰ+AのB問題解説(新課程2022年以降)#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
散布図は、K市のある月の30日間について、日ごとの最低気温を横軸、最高気温を縦軸にとったものである。この散布図から読み取れる内容として正しくないものを、次の①~⑥から3つ選べ。
① 最低気温が上がるにつれて最高気温も上がる傾向にある。
② 最高気温が15℃以下である日は、全部で8日以上ある。
③ 最低気温の範囲より最高気温の範囲の方が小さい。
④ 最低気温は10℃を超える日の最高気温は、すべて18℃以上である。
⑤ 最低気温が最も高い日の最高気温は24℃未満である。
⑥ 最低気温と最高気温の間には負の相関関係がある。
この動画を見る
散布図は、K市のある月の30日間について、日ごとの最低気温を横軸、最高気温を縦軸にとったものである。この散布図から読み取れる内容として正しくないものを、次の①~⑥から3つ選べ。
① 最低気温が上がるにつれて最高気温も上がる傾向にある。
② 最高気温が15℃以下である日は、全部で8日以上ある。
③ 最低気温の範囲より最高気温の範囲の方が小さい。
④ 最低気温は10℃を超える日の最高気温は、すべて18℃以上である。
⑤ 最低気温が最も高い日の最高気温は24℃未満である。
⑥ 最低気温と最高気温の間には負の相関関係がある。
【数Ⅰ】間違えやすい? 分散の公式の覚え方

【ユースケ・マセマティックがていねいに解説】データの分析 4S数学問題集数Ⅰ 341 変量変換2

単元:
#数Ⅰ#データの分析#データの分析#数学(高校生)
教材:
#4S数学#4S数学Ⅰ+AのB問題解説(新課程2022年以降)#データの分析#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
変量xのデータが次のように与えられている。
672, 693, 644, 665, 630, 644
c=7 , x₀=644 ,u=(x-x₀)/cとして新たな変量uを作る。
(1)変量uのデータの平均値、分散、標準偏差を求めよ。
(2)変量xのデータの平均値、分散、標準偏差を求めよ。
この動画を見る
変量xのデータが次のように与えられている。
672, 693, 644, 665, 630, 644
c=7 , x₀=644 ,u=(x-x₀)/cとして新たな変量uを作る。
(1)変量uのデータの平均値、分散、標準偏差を求めよ。
(2)変量xのデータの平均値、分散、標準偏差を求めよ。
【ユースケ・マセマティックがていねいに解説】データの分析 4S数学問題集数Ⅰ 339,340 変量変換

単元:
#数Ⅰ#データの分析#データの分析#数学(高校生)
教材:
#4S数学#4S数学Ⅰ+AのB問題解説(新課程2022年以降)#データの分析#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
変量xのデータの平均値$\bar{ x }$が35、分散$S_{ x }^2$が16であるとする。この時、次の式によって得られる新しい変量yのデータについて、平均$\bar{ y }$,分散$S_{ y }^2$,標準偏差$S_{ y }$を求めよ。
(1)$y=x-10$
(2)$y=3x$
(3)$y=-\frac{1}{2}x+6$
あるクラスの生徒を対象に100点満点の試験を行ったところ,平均値は68点,分散は36であった。得点調整のため,生徒全員の得点を2.5倍して,更に30点を加えたとき,得点調整後の平均値,分散,標準偏差を求めよ。
この動画を見る
変量xのデータの平均値$\bar{ x }$が35、分散$S_{ x }^2$が16であるとする。この時、次の式によって得られる新しい変量yのデータについて、平均$\bar{ y }$,分散$S_{ y }^2$,標準偏差$S_{ y }$を求めよ。
(1)$y=x-10$
(2)$y=3x$
(3)$y=-\frac{1}{2}x+6$
あるクラスの生徒を対象に100点満点の試験を行ったところ,平均値は68点,分散は36であった。得点調整のため,生徒全員の得点を2.5倍して,更に30点を加えたとき,得点調整後の平均値,分散,標準偏差を求めよ。
【ユースケ・マセマティックがていねいに解説】データの分析 4S数学問題集数Ⅰ 338 不明なデータがある場合の問題

単元:
#数Ⅰ#データの分析#データの分析#数学(高校生)
教材:
#4S数学#4S数学Ⅰ+AのB問題解説(新課程2022年以降)#データの分析#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
次のデータは、あるパズルに挑戦した10人について、完成するまでにかかった時間$x$(分)をまとめたものである。ただし、$x$のデータの平均値を$\bar{ x }$で表し、20分を超えた人はいなかったもののとする。次の問いに答えよ。
番号 1 2 3 4 5 6 7 8 9 10
$x$ 13 a 7 3 11 18 7 b 16 3
$(x-\bar{ x })² $ 4 c 16 64 0 d 16 1 25 64
(1)$\bar{ x }$の値を求めよ。
(2)$a$を$b$の式で表せ。
(3) $a$、$b$、$c$、$d$の値を求めよ。
(4)$x$の分散と標準偏差を求めよ。ただし小数第1位を四捨五入せよ。
この動画を見る
次のデータは、あるパズルに挑戦した10人について、完成するまでにかかった時間$x$(分)をまとめたものである。ただし、$x$のデータの平均値を$\bar{ x }$で表し、20分を超えた人はいなかったもののとする。次の問いに答えよ。
番号 1 2 3 4 5 6 7 8 9 10
$x$ 13 a 7 3 11 18 7 b 16 3
$(x-\bar{ x })² $ 4 c 16 64 0 d 16 1 25 64
(1)$\bar{ x }$の値を求めよ。
(2)$a$を$b$の式で表せ。
(3) $a$、$b$、$c$、$d$の値を求めよ。
(4)$x$の分散と標準偏差を求めよ。ただし小数第1位を四捨五入せよ。
【ユースケ・マセマティックがていねいに解説】データの分析 4S数学問題集数Ⅰ 337 データが変更されたときの平均、分散の関係

単元:
#数Ⅰ#データの分析#データの分析#数学(高校生)
教材:
#4S数学#4S数学Ⅰ+AのB問題解説(新課程2022年以降)#データの分析#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
次のデータは、ある6人について、懸垂が何回できたかを記録したものである。
14 11 10 18 16 9(単位は回)
(1) このデータの平均値を求めよ。
(2) このデータには記録ミスがあり、18回は正しくは17回、9回は正しくは10回であった。この誤りを修正した時、このデータの平均値、分散は、修正前から増加するか、減少するか、変化しないかを答えよ。
(3)(2)の修正後、他の1人の生徒について同じように懸垂の記録を取ったところ、13回であった。この生徒を加えた7人のデータの分散は、加える前と比較して増加するか、減少するか、変化しないかを答えよ。
この動画を見る
次のデータは、ある6人について、懸垂が何回できたかを記録したものである。
14 11 10 18 16 9(単位は回)
(1) このデータの平均値を求めよ。
(2) このデータには記録ミスがあり、18回は正しくは17回、9回は正しくは10回であった。この誤りを修正した時、このデータの平均値、分散は、修正前から増加するか、減少するか、変化しないかを答えよ。
(3)(2)の修正後、他の1人の生徒について同じように懸垂の記録を取ったところ、13回であった。この生徒を加えた7人のデータの分散は、加える前と比較して増加するか、減少するか、変化しないかを答えよ。
【ユースケ・マセマティックがていねいに解説】データの分析 4S数学問題集数Ⅰ 336 平均と分散だけ与えられたデータ

単元:
#数Ⅰ#データの分析#データの分析#数学(高校生)
教材:
#4S数学#4S数学Ⅰ+AのB問題解説(新課程2022年以降)#データの分析#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
次のデータは、ある6人について、懸垂が何回できたかを記録したものである。
14 11 10 18 16 9(単位は回)
(1) このデータの平均値を求めよ。
(2) このデータには記録ミスがあり、18回は正しくは17回、9回は正しくは10回であった。この誤りを修正した時、このデータの平均値、分散は、修正前から増加するか、減少するか、変化しないかを答えよ。
(3)(2)の修正後、他の1人の生徒について同じように懸垂の記録を取ったところ、13回であった。この生徒を加えた7人のデータの分散は、加える前と比較して増加するか、減少するか、変化しないかを答えよ。
この動画を見る
次のデータは、ある6人について、懸垂が何回できたかを記録したものである。
14 11 10 18 16 9(単位は回)
(1) このデータの平均値を求めよ。
(2) このデータには記録ミスがあり、18回は正しくは17回、9回は正しくは10回であった。この誤りを修正した時、このデータの平均値、分散は、修正前から増加するか、減少するか、変化しないかを答えよ。
(3)(2)の修正後、他の1人の生徒について同じように懸垂の記録を取ったところ、13回であった。この生徒を加えた7人のデータの分散は、加える前と比較して増加するか、減少するか、変化しないかを答えよ。
データの分析 4S数学問題集数Ⅰ 333 ヒストグラムと箱ひげ図2【ユースケ・マセマティックがていねいに解説】

単元:
#数Ⅰ#データの分析#データの分析#数学(高校生)
教材:
#4S数学#4S数学Ⅰ+AのB問題解説(新課程2022年以降)#データの分析#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
下のヒストグラムは、A市のある月の30日の日ごとの最高気温のデータを集めたものである。A市に対応する箱ひげ図を次の①~④の中から選べ。
この動画を見る
下のヒストグラムは、A市のある月の30日の日ごとの最高気温のデータを集めたものである。A市に対応する箱ひげ図を次の①~④の中から選べ。
【ユースケ・マセマティックがていねいに解説】データの分析 4S数学問題集数Ⅰ 326 欠けたデータの推測

単元:
#数Ⅰ#データの分析#データの分析#数学(高校生)
教材:
#4S数学#4S数学Ⅰ+AのB問題解説(新課程2022年以降)#データの分析#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
次のデータは、ある8店舗での1kgあたりのみかんの価格である。ただし、aの値は0以上の整数である。
525 550 498 550 555 500 a (単位は円)
(1)aの値がわからないとき、このデータの中央値として何通りの値があり得るか。
(2)このデータの平均値が535円であるとき、このデータの中央値を求めよ。
この動画を見る
次のデータは、ある8店舗での1kgあたりのみかんの価格である。ただし、aの値は0以上の整数である。
525 550 498 550 555 500 a (単位は円)
(1)aの値がわからないとき、このデータの中央値として何通りの値があり得るか。
(2)このデータの平均値が535円であるとき、このデータの中央値を求めよ。
【ユースケ・マセマティックがていねいに解説】データの分析 4S数学問題集数Ⅰ 325 データの中に誤りがあった場合

単元:
#数Ⅰ#データの分析#データの分析#数学(高校生)
教材:
#4S数学#4S数学Ⅰ+AのB問題解説(新課程2022年以降)#データの分析#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
ある高校で、エコ活動としてペットボトルのキャップを集めている。次のデータは、1か月ごとに集まったキャップの重量を半年間記録したものである。
3.2 1.2 2.3 2.0 2.7 2.4 (単位はkg)
(1)中央値と平均値を求めよ。
(2)上記の6個のうち1個が誤りであることが分かった。正しい数値に基づく中央値と平均値は、それぞれ2.55kgと2.4kgであるという。誤っている数値を選び、正しい数値を求めよ。
この動画を見る
ある高校で、エコ活動としてペットボトルのキャップを集めている。次のデータは、1か月ごとに集まったキャップの重量を半年間記録したものである。
3.2 1.2 2.3 2.0 2.7 2.4 (単位はkg)
(1)中央値と平均値を求めよ。
(2)上記の6個のうち1個が誤りであることが分かった。正しい数値に基づく中央値と平均値は、それぞれ2.55kgと2.4kgであるという。誤っている数値を選び、正しい数値を求めよ。
【ユースケ・マセマティックがていねいに解説】データの分析 4S数学問題集数Ⅰ 324 度数分布表

単元:
#数Ⅰ#データの分析#データの分析#数学(高校生)
教材:
#4S数学#4S数学Ⅰ+AのB問題解説(新課程2022年以降)#データの分析#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
右の表は25人の生徒のテストの得点のデータから作った度数分布表である。
(1)このデータの平均値のとり得る範囲を求めよ。
(2)60点以上69点以下の階級に含まれる値が次ののようであるとき、全体のデータの中央値を求めよ。
68 63 66 62 68 63 67 65
この動画を見る
右の表は25人の生徒のテストの得点のデータから作った度数分布表である。
(1)このデータの平均値のとり得る範囲を求めよ。
(2)60点以上69点以下の階級に含まれる値が次ののようであるとき、全体のデータの中央値を求めよ。
68 63 66 62 68 63 67 65
【ユースケ・マセマティックがていねいに解説】データの分析 4S数学問題集数Ⅰ 323 平均点からデータを求める

単元:
#数Ⅰ#データの分析#データの分析#数学(高校生)
教材:
#4S数学#4S数学Ⅰ+AのB問題解説(新課程2022年以降)#データの分析#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
次のデータは、ある体操競技会に参加した10人のある種目の得点である。
13.2 13.0 13.7 12.5 14.6 12.3 12.5 11.9 13.9 a (単位は点)
このデータの平均値が13.1点であるとき、aの値を求めよ。
この動画を見る
次のデータは、ある体操競技会に参加した10人のある種目の得点である。
13.2 13.0 13.7 12.5 14.6 12.3 12.5 11.9 13.9 a (単位は点)
このデータの平均値が13.1点であるとき、aの値を求めよ。
【短時間でマスター!!】分散・標準偏差の求め方を解説!〔現役塾講師解説、数学〕

単元:
#数Ⅰ#データの分析#データの分析#数学(高校生)
指導講師:
3rd School
問題文全文(内容文):
数学1A
分散・標準偏差
3,7,9,6,4,7
①分散
②標準偏差
この動画を見る
数学1A
分散・標準偏差
3,7,9,6,4,7
①分散
②標準偏差
【短時間でマスター!!】四分位数・四分位範囲・四分位偏差の求め方を解説!〔現役塾講師解説、数学〕

算数できない投資情報誌の記者の記事が医大の入試問題に 小学生もチャレンジしてね!
単元:
#数Ⅰ#大学入試過去問(数学)#データの分析#データの分析#学校別大学入試過去問解説(数学)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
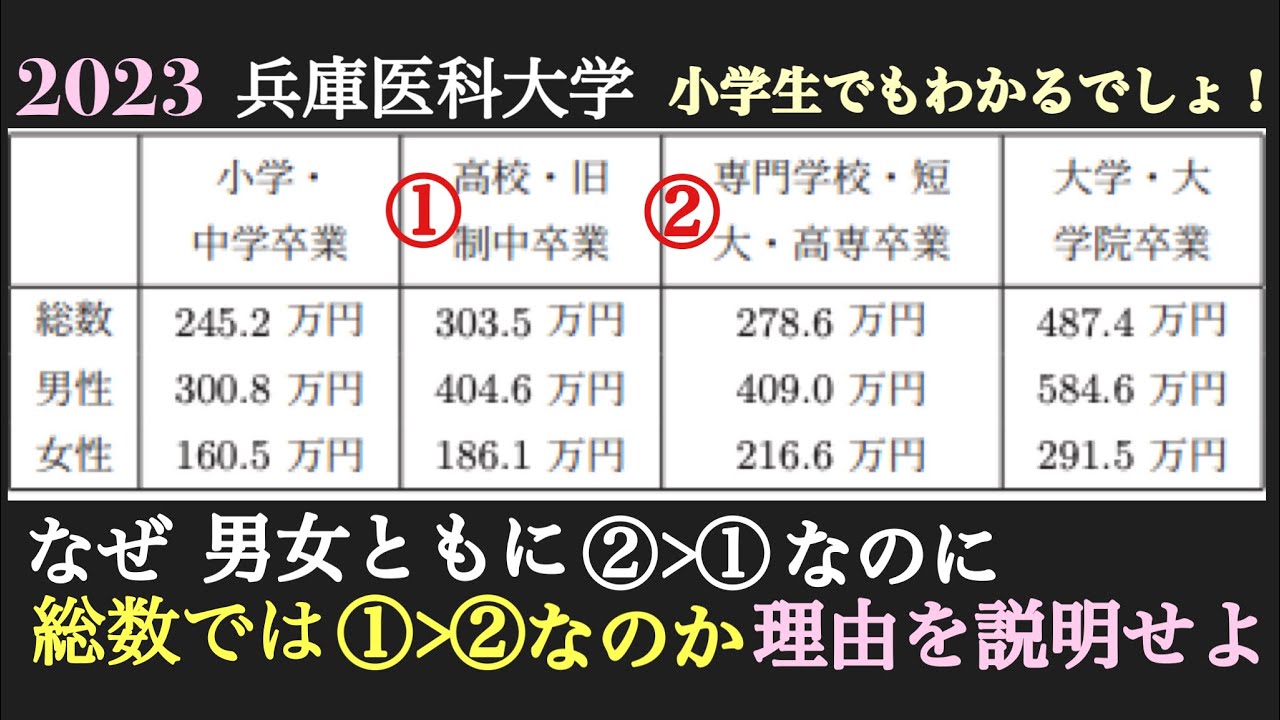
$次の文章は,「貯蓄額や所得の多い少ないは「学歴」と関係あるのか?」という記事^1からの抜粋である。表は厚生労働省の令和元年国民生活基礎調査から,学歴ごとの平均所得金額(15歳以上の雇用者1人あたり)をまとめたものです。(中略)
男性・女性ともに専門学校・短大・高専卒の方が所得金額が多いのに,総数となると高校・旧制中卒の方が多いのは統計上の謎です。
男性の所得金額も女性の所得金額もともに,専門学校・短大・高専卒業の方が,高校・旧制中卒業より多いのに,総数(男性+女性)では,逆転した結果になっている。これはどうしてか?説明しなさい。$
この動画を見る
$次の文章は,「貯蓄額や所得の多い少ないは「学歴」と関係あるのか?」という記事^1からの抜粋である。表は厚生労働省の令和元年国民生活基礎調査から,学歴ごとの平均所得金額(15歳以上の雇用者1人あたり)をまとめたものです。(中略)
男性・女性ともに専門学校・短大・高専卒の方が所得金額が多いのに,総数となると高校・旧制中卒の方が多いのは統計上の謎です。
男性の所得金額も女性の所得金額もともに,専門学校・短大・高専卒業の方が,高校・旧制中卒業より多いのに,総数(男性+女性)では,逆転した結果になっている。これはどうしてか?説明しなさい。$
福田の数学〜立教大学2022年経済学部第1問(6)〜平均と分散

福田の数学〜慶應義塾大学2022年看護医療学部第3問〜平均と分散の変換

単元:
#数Ⅰ#大学入試過去問(数学)#データの分析#データの分析#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
\begin{eqnarray}
{\large\boxed{3}}\ (1)ある学校で100点満点のテストを行うことになった。\\
まず10人の教員で解いてみたところ、その得点のヒストグラムは\\
右図(※動画参照)のようになった。ただし、得点は整数値とする。\\
このデータの平均値は\boxed{\ \ ア\ \ }\ 点、中央値は\boxed{\ \ イ\ \ }\ 点、\\
最頻値は\boxed{\ \ ウ\ \ }\ 点、分散は\boxed{\ \ エ\ \ }\ 点である。\\
(2)A組とB組の2つのクラスで数学のテストを行ったところ、A組の得点の平均\\
値が\overline{x}_A、分散がs_A^2、B組の得点の平均値が\overline{x}_B、分散がs_B^2となった。\\
ただし、\overline{x}_A,\overline{x}_B,s_A^2,s_B^2はいずれも0ではなかった。このとき、B組の各生徒\\
の得点xに対して、正の実数aと実数bを用いてy=ax+bと変換し、\\
yの平均値と分散をA組の平均値と分散に一致させるためには、\\
a=\boxed{\ \ オ\ \ }、b=\boxed{\ \ カ\ \ }とすればよい。
\end{eqnarray}
この動画を見る
\begin{eqnarray}
{\large\boxed{3}}\ (1)ある学校で100点満点のテストを行うことになった。\\
まず10人の教員で解いてみたところ、その得点のヒストグラムは\\
右図(※動画参照)のようになった。ただし、得点は整数値とする。\\
このデータの平均値は\boxed{\ \ ア\ \ }\ 点、中央値は\boxed{\ \ イ\ \ }\ 点、\\
最頻値は\boxed{\ \ ウ\ \ }\ 点、分散は\boxed{\ \ エ\ \ }\ 点である。\\
(2)A組とB組の2つのクラスで数学のテストを行ったところ、A組の得点の平均\\
値が\overline{x}_A、分散がs_A^2、B組の得点の平均値が\overline{x}_B、分散がs_B^2となった。\\
ただし、\overline{x}_A,\overline{x}_B,s_A^2,s_B^2はいずれも0ではなかった。このとき、B組の各生徒\\
の得点xに対して、正の実数aと実数bを用いてy=ax+bと変換し、\\
yの平均値と分散をA組の平均値と分散に一致させるためには、\\
a=\boxed{\ \ オ\ \ }、b=\boxed{\ \ カ\ \ }とすればよい。
\end{eqnarray}
福田の数学〜慶應義塾大学2022年薬学部第3問〜データの分析・平均・標準偏差・共分散・相関係数
単元:
#数Ⅰ#大学入試過去問(数学)#データの分析#データの分析#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
\begin{eqnarray}
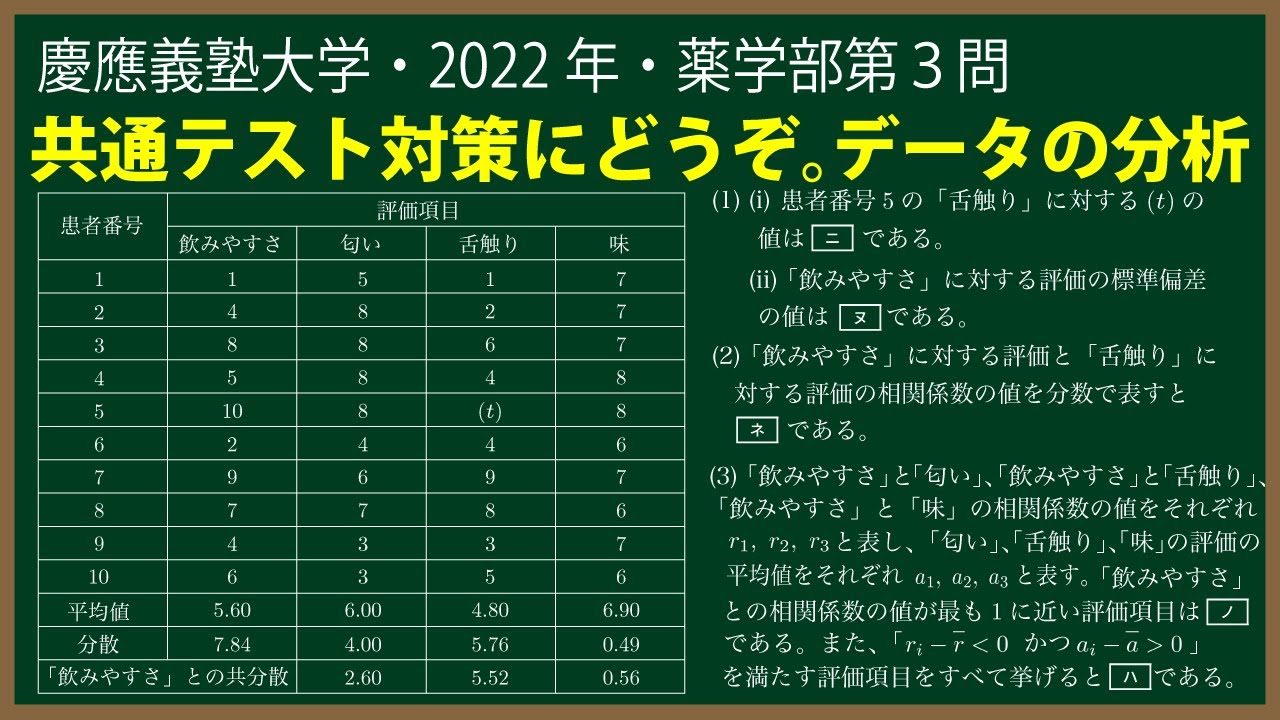
{\Large\boxed{3}}\ ある病院の入院患者10人に対して、病院内で作っている粉薬の評価を調査した。\hspace{50pt}\\
調査の評価項目は、粉薬の「飲みやすさ」と、「飲みやすさ」の要因と考えられる\\
「匂い」「舌触り」、「味」の計4項目についてである。\\
10人の患者が、評価項目について最も満足な場合は10、最も不安な場合は1として、\\
1以上10以下の整数で評価した。表内の平均値、分散、共分散の数値は四捨五入\\
されていない正確な値である。(※動画参照)\\
「飲みやすさ」との共分散は、「飲みやすさ」に対する評価の偏差と、各評価項目\\
に対する評価の偏差の積の平均値である。\\
(1)(\textrm{i})患者番号5の「舌触り」に対する(t)の値は\boxed{\ \ ニ\ \ }である。\\
(\textrm{ii})「飲みやすさ」に対する評価の標準偏差の値は\boxed{\ \ ヌ\ \ }である。\\
(2)「飲みやすさ」に対する評価と「舌触り」に対する評価の相関係数の値を\\
分数で表すと\boxed{\ \ ネ\ \ }である。\\
(3)「飲みやすさ」と「匂い」、「飲みやすさ」と「舌触り」、「飲みやすさ」と「味」\\
の相関係数の値をそれぞれr_1,r_2,r_3と表し、「匂い」、「舌触り」、「味」の評価の\\
平均値をそれぞれa_1,a_2,a_3と表す。a_i,r_i (1 \leqq i \leqq 3)に対し、\bar{ r }と\bar{ a }は以下の式で定める。\\
\bar{ r }=\frac{r_1+r_2+r_3}{3}, \bar{ a }=\frac{a_1+a_2+a_3}{3}\\
「飲みやすさ」との相関係数の値が最も1に近い評価項目は\ \boxed{\ \ ノ\ \ }\ である。\\
また、「r_i-\bar{ r } \lt0かつa_i-\bar{ a } \gt0」を満たす評価項目をすべて挙げると\ \boxed{\ \ ノ\ \ }\ である。\\
\\
(4)「匂い」、「舌触り」、「味」のうち、\ \boxed{\ \ ハ\ \ }\ にあてはまらない評価項目\\
(以降、この評価項目をXと表す)に関して改良を行った。改良後の紛薬に対して、同じ10人の\\
患者がXと「飲みやすさ」について再び評価した。\\
改良後の調査結果では、Xの評価は10人全員の評価が改良前に比べてそれぞれ1上がっていた。\\
改良後のXの評価の平均値を求めると\ \boxed{\ \ ヒ\ \ }\ であり、標準偏差は改良前調査における値と\\
比べて\ \boxed{\ \ フ\ \ }\ 。また、「飲みやすさ」の評価については、改良前の調査において評価が\\
1以上4以下の場合は2上がり、5以上9以下の場合は1上がり、10の場合は評価が変わらず\\
10であった。よって改良後の「飲みやすさ」に対する評価の平均値を求めると\ \boxed{\ \ ヘ\ \ }\ であり、\\
標準偏差は改良前の調査における値と比べて\ \boxed{\ \ ホ\ \ }。\\
\end{eqnarray}
この動画を見る
\begin{eqnarray}
{\Large\boxed{3}}\ ある病院の入院患者10人に対して、病院内で作っている粉薬の評価を調査した。\hspace{50pt}\\
調査の評価項目は、粉薬の「飲みやすさ」と、「飲みやすさ」の要因と考えられる\\
「匂い」「舌触り」、「味」の計4項目についてである。\\
10人の患者が、評価項目について最も満足な場合は10、最も不安な場合は1として、\\
1以上10以下の整数で評価した。表内の平均値、分散、共分散の数値は四捨五入\\
されていない正確な値である。(※動画参照)\\
「飲みやすさ」との共分散は、「飲みやすさ」に対する評価の偏差と、各評価項目\\
に対する評価の偏差の積の平均値である。\\
(1)(\textrm{i})患者番号5の「舌触り」に対する(t)の値は\boxed{\ \ ニ\ \ }である。\\
(\textrm{ii})「飲みやすさ」に対する評価の標準偏差の値は\boxed{\ \ ヌ\ \ }である。\\
(2)「飲みやすさ」に対する評価と「舌触り」に対する評価の相関係数の値を\\
分数で表すと\boxed{\ \ ネ\ \ }である。\\
(3)「飲みやすさ」と「匂い」、「飲みやすさ」と「舌触り」、「飲みやすさ」と「味」\\
の相関係数の値をそれぞれr_1,r_2,r_3と表し、「匂い」、「舌触り」、「味」の評価の\\
平均値をそれぞれa_1,a_2,a_3と表す。a_i,r_i (1 \leqq i \leqq 3)に対し、\bar{ r }と\bar{ a }は以下の式で定める。\\
\bar{ r }=\frac{r_1+r_2+r_3}{3}, \bar{ a }=\frac{a_1+a_2+a_3}{3}\\
「飲みやすさ」との相関係数の値が最も1に近い評価項目は\ \boxed{\ \ ノ\ \ }\ である。\\
また、「r_i-\bar{ r } \lt0かつa_i-\bar{ a } \gt0」を満たす評価項目をすべて挙げると\ \boxed{\ \ ノ\ \ }\ である。\\
\\
(4)「匂い」、「舌触り」、「味」のうち、\ \boxed{\ \ ハ\ \ }\ にあてはまらない評価項目\\
(以降、この評価項目をXと表す)に関して改良を行った。改良後の紛薬に対して、同じ10人の\\
患者がXと「飲みやすさ」について再び評価した。\\
改良後の調査結果では、Xの評価は10人全員の評価が改良前に比べてそれぞれ1上がっていた。\\
改良後のXの評価の平均値を求めると\ \boxed{\ \ ヒ\ \ }\ であり、標準偏差は改良前調査における値と\\
比べて\ \boxed{\ \ フ\ \ }\ 。また、「飲みやすさ」の評価については、改良前の調査において評価が\\
1以上4以下の場合は2上がり、5以上9以下の場合は1上がり、10の場合は評価が変わらず\\
10であった。よって改良後の「飲みやすさ」に対する評価の平均値を求めると\ \boxed{\ \ ヘ\ \ }\ であり、\\
標準偏差は改良前の調査における値と比べて\ \boxed{\ \ ホ\ \ }。\\
\end{eqnarray}
ここ分からんかったやろ?

単元:
#数学(中学生)#中1数学#数Ⅰ#資料の活用#データの分析#データの分析#数学(高校生)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
四分位数
四分位範囲
箱ひげ図
解説動画です
この動画を見る
四分位数
四分位範囲
箱ひげ図
解説動画です
福田の共通テスト解答速報〜2022年共通テスト数学IA問題2[2]。データの分析の問題。

単元:
#数Ⅰ#大学入試過去問(数学)#データの分析#データの分析#センター試験・共通テスト関連#共通テスト#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
\begin{eqnarray}
[2] 日本国外における日本語教育の状況を調べるために、独立行政法人国際交流基金では\\
「海外日本教育機関調査」を実施しており、各国における教育機関数,教員数,学習数\\
が調べられている。2018年度において学習者数が5000人以上の国と地域(以下、国)\\
は29ヵ国であった。これら29ヵ国について、2009年度と2018年度のデータが得られている。\\
\\
\\
(1) 各国において、学習者数を教員数で割ることにより、国ごとの\\
「教員1人当たりの学習者数」を算出することができる。図1と図2(※動画参照)は、\\
2009年度および2018年度における「教員1人当たりの学習者数」のヒストグラム\\
である。これら二つのヒストグラムから、9年間の変化に関して、後のことが読み取れる。\\
なお、ヒストグラムの各階級の区間は、左側の数値を含み、右側の数値を含まない。\\
\\
\\
・2009年度と2018年度の中央値が含まれる階級の階級値を比較すると、\boxed{\ \ ケ\ \ }\\
・2009年度と2018年度の第1四分位数が含まれる階級の階級値を比較すると、\boxed{\ \ コ\ \ }\\
・2009年度と2018年度の第3四分位数が含まれる階級の階級値を比較すると、\boxed{\ \ サ\ \ }\\
・2009年度と2018年度の範囲を比較すると、\boxed{\ \ シ\ \ }。\\
・2009年度と2018年度の四分位範囲を比較すると、\boxed{\ \ ス\ \ }。\\
\\
\boxed{\ \ ケ\ \ }~\boxed{\ \ ス\ \ }を次の⓪~③のうちから一つ選べ。\\
⓪ 2018年度の方が小さい\\
① 2018年度の方が大きい\\
② 両者は等しい\\
③ これら二つのヒストグラムからだけでは両者の大小を判断できない\\
\\
\\
(2)各国において、学習者数を教育機関数で割ることにより、「教育機関1機関あたりの\\
学習者数」も算出した。図3(※動画参照)は、2009年度における\\
「教育機関1機関あたりの学習者数」の箱ひげ図である。\\
\\
2009年度について、「教育機関1機関あたりの学習者数」(横軸)と\\
「教員1人当たりの学習者数」(縦軸)の散布図は\boxed{\ \ セ\ \ }である。ここで、\\
2009年度における「教員1人当たりの学習者数」のヒストグラムである(1)の図1\\
を、図4(※動画参照)として再掲しておく。\\
\\
\boxed{\ \ セ\ \ }については、最も適当なものを、次の⓪~③のうちから一つ選べ。\\
なお、これらの散布図には、完全に重なっている点はない。\\
(※選択肢は動画参照)\\
\\
(3) 各国における2018年度の学習者数を100としたときの2009年度の学習者数S,\\
および、各国における2018年度の教員数を100としたときの2009年度の\\
教員数Tを算出した。\\
例えば、学習者数について説明すると、ある国において、2009年度が44272人,\\
2018年度が174521人であった場合、2009年度の学習者数Sは\\
\frac{44272}{174521}×100 より25.4と算出される。\\
表1(※動画参照)はSとTについて、平均値、標準偏差および共分散を計算したものである。\\
ただし、SとTの共分散は、Sの偏差とTの偏差の積の平均値である。\\
表1の数値が四捨五入していない正確な値であるとして、SとTの相関係数\\
を求めると\boxed{\ \ ソ\ \ }, \boxed{\ \ タチ\ \ } である。\\
\\
(4) 表1と(3)で求めた相関係数を参考にすると、(3)で算出した2009年度の\\
S(横軸)とT(縦軸)の散布図は\boxed{\ \ ツ\ \ }である。\\
\\
\boxed{\ \ ツ\ \ }については、最も適当なものを、次の⓪~③のうちから一つ\\
選べ。なお、これらの散布図には、完全に重なっている点はない。\\
(※選択肢は動画参照)
\end{eqnarray}
この動画を見る
\begin{eqnarray}
[2] 日本国外における日本語教育の状況を調べるために、独立行政法人国際交流基金では\\
「海外日本教育機関調査」を実施しており、各国における教育機関数,教員数,学習数\\
が調べられている。2018年度において学習者数が5000人以上の国と地域(以下、国)\\
は29ヵ国であった。これら29ヵ国について、2009年度と2018年度のデータが得られている。\\
\\
\\
(1) 各国において、学習者数を教員数で割ることにより、国ごとの\\
「教員1人当たりの学習者数」を算出することができる。図1と図2(※動画参照)は、\\
2009年度および2018年度における「教員1人当たりの学習者数」のヒストグラム\\
である。これら二つのヒストグラムから、9年間の変化に関して、後のことが読み取れる。\\
なお、ヒストグラムの各階級の区間は、左側の数値を含み、右側の数値を含まない。\\
\\
\\
・2009年度と2018年度の中央値が含まれる階級の階級値を比較すると、\boxed{\ \ ケ\ \ }\\
・2009年度と2018年度の第1四分位数が含まれる階級の階級値を比較すると、\boxed{\ \ コ\ \ }\\
・2009年度と2018年度の第3四分位数が含まれる階級の階級値を比較すると、\boxed{\ \ サ\ \ }\\
・2009年度と2018年度の範囲を比較すると、\boxed{\ \ シ\ \ }。\\
・2009年度と2018年度の四分位範囲を比較すると、\boxed{\ \ ス\ \ }。\\
\\
\boxed{\ \ ケ\ \ }~\boxed{\ \ ス\ \ }を次の⓪~③のうちから一つ選べ。\\
⓪ 2018年度の方が小さい\\
① 2018年度の方が大きい\\
② 両者は等しい\\
③ これら二つのヒストグラムからだけでは両者の大小を判断できない\\
\\
\\
(2)各国において、学習者数を教育機関数で割ることにより、「教育機関1機関あたりの\\
学習者数」も算出した。図3(※動画参照)は、2009年度における\\
「教育機関1機関あたりの学習者数」の箱ひげ図である。\\
\\
2009年度について、「教育機関1機関あたりの学習者数」(横軸)と\\
「教員1人当たりの学習者数」(縦軸)の散布図は\boxed{\ \ セ\ \ }である。ここで、\\
2009年度における「教員1人当たりの学習者数」のヒストグラムである(1)の図1\\
を、図4(※動画参照)として再掲しておく。\\
\\
\boxed{\ \ セ\ \ }については、最も適当なものを、次の⓪~③のうちから一つ選べ。\\
なお、これらの散布図には、完全に重なっている点はない。\\
(※選択肢は動画参照)\\
\\
(3) 各国における2018年度の学習者数を100としたときの2009年度の学習者数S,\\
および、各国における2018年度の教員数を100としたときの2009年度の\\
教員数Tを算出した。\\
例えば、学習者数について説明すると、ある国において、2009年度が44272人,\\
2018年度が174521人であった場合、2009年度の学習者数Sは\\
\frac{44272}{174521}×100 より25.4と算出される。\\
表1(※動画参照)はSとTについて、平均値、標準偏差および共分散を計算したものである。\\
ただし、SとTの共分散は、Sの偏差とTの偏差の積の平均値である。\\
表1の数値が四捨五入していない正確な値であるとして、SとTの相関係数\\
を求めると\boxed{\ \ ソ\ \ }, \boxed{\ \ タチ\ \ } である。\\
\\
(4) 表1と(3)で求めた相関係数を参考にすると、(3)で算出した2009年度の\\
S(横軸)とT(縦軸)の散布図は\boxed{\ \ ツ\ \ }である。\\
\\
\boxed{\ \ ツ\ \ }については、最も適当なものを、次の⓪~③のうちから一つ\\
選べ。なお、これらの散布図には、完全に重なっている点はない。\\
(※選択肢は動画参照)
\end{eqnarray}
【数Ⅰ】データの分析:標準得点について

単元:
#数Ⅰ#データの分析#データの分析#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
【高校数学 数学Ⅰ データの分析】
標準得点(Z得点)と呼ばれる調整された得点の計算方法と、その特徴について説明をします。
共通テストの模試や私大の入試にも良く出題されるテーマですので、この機会にぜひマスターしておきましょう!
この動画を見る
【高校数学 数学Ⅰ データの分析】
標準得点(Z得点)と呼ばれる調整された得点の計算方法と、その特徴について説明をします。
共通テストの模試や私大の入試にも良く出題されるテーマですので、この機会にぜひマスターしておきましょう!
福田の共通テスト直前演習〜2021年共通テスト数学IA問題2[2]。データの分析の問題。

単元:
#数Ⅰ#大学入試過去問(数学)#データの分析#データの分析#センター試験・共通テスト関連#共通テスト#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
\begin{eqnarray}
{\Large\boxed{2}} [2]就業者の従事する産業は第1次産業、第2次産業、第3次産業の三つに分類される。\\
都道府県別に、就業者数に対する各産業に就業する人数の割合を、\\
各産業の「就業者数割合」と呼ぶことにする。\\
\\
(1)図1(※動画参照)は、1975年から2010年まで5年ごとの8個の年度(それ\\
ぞれを時点という)における都道府県別の三つの産業の就業者\\
数割合を箱ひげ図で表したものである。各時点の箱ひげ図は、\\
それぞれ上から第1次産業、第2次産業、第3次産業である。 \\
次の①~⑤のうち、図1から読み取れることとして正しくない\\
ものは\boxed{\ \ タ\ \ }と\boxed{\ \ チ\ \ }である。\\
\\
タ、チの解答群\\
\\
⓪ 第1次産業の就業者数割合の四分位範囲は、2000年までは\\
後の時点になるにしたがって減少している。\\
① 第1次産業の就業者数割合について、左側のひげの長さと右側\\
のひげの長さを比較すると、どの時点においても左側の方が長い。\\
② 第2次産業の就業者数割合の中央値は、1990年以降、後の時点\\
になるにしたがって減少している。\\
③ 第2次産業の就業者数割合の第1四分位数は、後の時点にした\\
がって減少している。\\
④ 第3次産業の就業者数割合の第3四分位数は、後の時点にした\\
がって増加している。\\
⑤ 第3次産業の就業者数割合の最小値は、後の時点にしたがって増加している。\\
\\
\\
(2)(1)で取り上げた8時点の中から5時点を取り出して考える。\\
各時点における都道府県別の、第1次産業と第3次産業の就業\\
者数割合のヒストグラムを一つのグラフにまとめてかいたもの\\
が、右の5つのグラフである。それぞれの右側の網掛けした\\
ヒストグラムが第3次産業のものである。なお、ヒストグラム\\
の各階級の区間は、左側の数値を含み、右側の数値を含まない。\\
・1985年度におけるグラフは\boxed{\ \ ツ\ \ } である。\\
・1995年度におけるグラフは\boxed{\ \ テ\ \ } である。\\
\\
(※\boxed{\ \ ツ\ \ }, \boxed{\ \ テ\ \ }の選択肢は動画参照)\\
\\
(3) 三つの産業から二つずつを組み合わせて都道府県別の就業者数割合\\
の散布図を作成した。右の図2の散布\\
図群は、左から順に1975年度における第1次産業(横軸)と\\
第2次産業(縦軸)の散布図、第2次産業(横軸) \\
と第3次産業(縦軸)の散布図、第3次産業(横軸)と第1次産業(縦軸)の散布図である。\\
また、図3(※動画参照)は同様に作成した2015年度の散布図群である。\\
下の (\textrm{I})(\textrm{II})(\textrm{III}) は1975年度を基準にしたときの、\\
2015年度の変化を記述したものである。ただし、ここで\\
「相関が強くなった」とは、相関係数の絶対値が大きくなったことを意味する。\\
\\
(\textrm{I}) 都道府県別の第1次産業の就業者数割合と第2次産業\\
の就業者数割合の間の相関は強くなった。\\
(\textrm{II}) 都道府県別の第2次産業の就業者数割合と第3次産業\\
の就業者数割合の間の相関は強くなった。 \\
(\textrm{III}) 都道府県別の第3次産業の就業者数割合と第1次産業\\
の就業者数割合の間の相関は強くなった。\\
正誤の組み合わせとして正しいのは\boxed{\ \ ト\ \ }である。\\
(※\boxed{\ \ ト\ \ }の選択肢は動画参照)\\
\\
(4) 各都道府県の就業者数割合の内訳として男女別の\\
就業者数も発表されている。そこで、就業者数に対する\\
男性・女性の就業者数の割合をそれぞれ「男性の就業者数割合」、\\
「女性の就業者数割合」と呼ぶことにし、\\
これらを都道府県別に算出した、下の図4(※動画参照)は、2015年度における\\
都道府県別の、第1次産業の就業者数割合(横軸)、\\
男性の就業者数割合(縦軸)の散布図である。\\
各都道府県の、男性の就業者数と女性の就業者数を\\
合計すると就業者数の全体になることに注意すると、\\
2015年度における都道府県別の、第1次産業の就業者数割合(横軸)と、\\
女性の就業者数割合(縦軸)の 散布図は\boxed{\ \ ナ\ \ }である。\\
ナについては①~③のうちから 最も適当なものを一つ選べ。
\end{eqnarray}
この動画を見る
\begin{eqnarray}
{\Large\boxed{2}} [2]就業者の従事する産業は第1次産業、第2次産業、第3次産業の三つに分類される。\\
都道府県別に、就業者数に対する各産業に就業する人数の割合を、\\
各産業の「就業者数割合」と呼ぶことにする。\\
\\
(1)図1(※動画参照)は、1975年から2010年まで5年ごとの8個の年度(それ\\
ぞれを時点という)における都道府県別の三つの産業の就業者\\
数割合を箱ひげ図で表したものである。各時点の箱ひげ図は、\\
それぞれ上から第1次産業、第2次産業、第3次産業である。 \\
次の①~⑤のうち、図1から読み取れることとして正しくない\\
ものは\boxed{\ \ タ\ \ }と\boxed{\ \ チ\ \ }である。\\
\\
タ、チの解答群\\
\\
⓪ 第1次産業の就業者数割合の四分位範囲は、2000年までは\\
後の時点になるにしたがって減少している。\\
① 第1次産業の就業者数割合について、左側のひげの長さと右側\\
のひげの長さを比較すると、どの時点においても左側の方が長い。\\
② 第2次産業の就業者数割合の中央値は、1990年以降、後の時点\\
になるにしたがって減少している。\\
③ 第2次産業の就業者数割合の第1四分位数は、後の時点にした\\
がって減少している。\\
④ 第3次産業の就業者数割合の第3四分位数は、後の時点にした\\
がって増加している。\\
⑤ 第3次産業の就業者数割合の最小値は、後の時点にしたがって増加している。\\
\\
\\
(2)(1)で取り上げた8時点の中から5時点を取り出して考える。\\
各時点における都道府県別の、第1次産業と第3次産業の就業\\
者数割合のヒストグラムを一つのグラフにまとめてかいたもの\\
が、右の5つのグラフである。それぞれの右側の網掛けした\\
ヒストグラムが第3次産業のものである。なお、ヒストグラム\\
の各階級の区間は、左側の数値を含み、右側の数値を含まない。\\
・1985年度におけるグラフは\boxed{\ \ ツ\ \ } である。\\
・1995年度におけるグラフは\boxed{\ \ テ\ \ } である。\\
\\
(※\boxed{\ \ ツ\ \ }, \boxed{\ \ テ\ \ }の選択肢は動画参照)\\
\\
(3) 三つの産業から二つずつを組み合わせて都道府県別の就業者数割合\\
の散布図を作成した。右の図2の散布\\
図群は、左から順に1975年度における第1次産業(横軸)と\\
第2次産業(縦軸)の散布図、第2次産業(横軸) \\
と第3次産業(縦軸)の散布図、第3次産業(横軸)と第1次産業(縦軸)の散布図である。\\
また、図3(※動画参照)は同様に作成した2015年度の散布図群である。\\
下の (\textrm{I})(\textrm{II})(\textrm{III}) は1975年度を基準にしたときの、\\
2015年度の変化を記述したものである。ただし、ここで\\
「相関が強くなった」とは、相関係数の絶対値が大きくなったことを意味する。\\
\\
(\textrm{I}) 都道府県別の第1次産業の就業者数割合と第2次産業\\
の就業者数割合の間の相関は強くなった。\\
(\textrm{II}) 都道府県別の第2次産業の就業者数割合と第3次産業\\
の就業者数割合の間の相関は強くなった。 \\
(\textrm{III}) 都道府県別の第3次産業の就業者数割合と第1次産業\\
の就業者数割合の間の相関は強くなった。\\
正誤の組み合わせとして正しいのは\boxed{\ \ ト\ \ }である。\\
(※\boxed{\ \ ト\ \ }の選択肢は動画参照)\\
\\
(4) 各都道府県の就業者数割合の内訳として男女別の\\
就業者数も発表されている。そこで、就業者数に対する\\
男性・女性の就業者数の割合をそれぞれ「男性の就業者数割合」、\\
「女性の就業者数割合」と呼ぶことにし、\\
これらを都道府県別に算出した、下の図4(※動画参照)は、2015年度における\\
都道府県別の、第1次産業の就業者数割合(横軸)、\\
男性の就業者数割合(縦軸)の散布図である。\\
各都道府県の、男性の就業者数と女性の就業者数を\\
合計すると就業者数の全体になることに注意すると、\\
2015年度における都道府県別の、第1次産業の就業者数割合(横軸)と、\\
女性の就業者数割合(縦軸)の 散布図は\boxed{\ \ ナ\ \ }である。\\
ナについては①~③のうちから 最も適当なものを一つ選べ。
\end{eqnarray}
福田の数学〜立教大学2021年経済学部第1問(6)〜平均と分散の関係

単元:
#数Ⅰ#大学入試過去問(数学)#データの分析#データの分析#学校別大学入試過去問解説(数学)#立教大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
\begin{eqnarray}
{\Large\boxed{1}} (6)\ 10個の正三角形がある。それらの辺の長さからなるデータの平均は9である。\\
また、それらの面積からなるデータの平均値は\frac{118\sqrt3}{5}である。このとき、\\
辺の長さからなるデータの分散は\ \boxed{\ \ ク\ \ }\ である。
\end{eqnarray}
この動画を見る
\begin{eqnarray}
{\Large\boxed{1}} (6)\ 10個の正三角形がある。それらの辺の長さからなるデータの平均は9である。\\
また、それらの面積からなるデータの平均値は\frac{118\sqrt3}{5}である。このとき、\\
辺の長さからなるデータの分散は\ \boxed{\ \ ク\ \ }\ である。
\end{eqnarray}
【数Ⅰ】データの分析の全用語を解説【これだけでデータの分析はバッチシ】

福田の数学〜明治大学2021年全学部統一入試IⅡAB第1問(3)〜九九の表の平均と分散

単元:
#数Ⅰ#大学入試過去問(数学)#データの分析#データの分析#学校別大学入試過去問解説(数学)#明治大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
\begin{eqnarray}
{\Large\boxed{1}} (3)\ 九九の表(1の段から9の段まで)に現れる81個の数の平均値\ \boxed{\ \ シス\ \ }\ であり、\\
分散は小数第一位を四捨五入して整数で求めると\ \boxed{\ \ セソタ\ \ }\ である。
\end{eqnarray}
この動画を見る
\begin{eqnarray}
{\Large\boxed{1}} (3)\ 九九の表(1の段から9の段まで)に現れる81個の数の平均値\ \boxed{\ \ シス\ \ }\ であり、\\
分散は小数第一位を四捨五入して整数で求めると\ \boxed{\ \ セソタ\ \ }\ である。
\end{eqnarray}
福田の数学〜慶應義塾大学2021年看護医療学部第3問〜散布図と箱ひげ図

単元:
#数Ⅰ#大学入試過去問(数学)#データの分析#データの分析#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
\begin{eqnarray}
{\Large\boxed{3}} ある高校の生徒30人に対し、50m走のタイムを2回計測した。\\
左図(※動画参照)は1回目の計測結果を横軸に2回目の計測結果\\
を縦軸に取った散布図である。\\
(1)次の(\textrm{A})から(\textrm{F})のうち、1回目の計測結果の箱ひげ図\\
として適当なものは\boxed{\ \ ネ\ \ }であり、2回目の計測結果の箱ひげ図として\\
適当なものは\boxed{\ \ ノ\ \ }である。\\
(2)次の(\textrm{G})から(\textrm{L})のうち、1回目と2回目の計測結果の合計の\\
箱ひげ図として適切なものは\boxed{\ \ ハ\ \ }である。\\
(3)遅れてやってきた31人目の生徒の50m走のタイムを2回計測した\\
結果、1回目は20.0(秒)、2回目は10.0(秒)であった。各生徒の2回の\\
計測結果の合計を考え、最初の30人の生徒の平均値を\bar{ x_{31} },中央値を\\
m_{31}とする。\bar{ x_{30} }=17.0であることに注意すると、\\
\bar{ x_{31} }-\bar{ x_{30} }=\boxed{\ \ ヒ\ \ }である。一方、\\
m_{31}-m_{30}=\boxed{\ \ フ\ \ }である。\\
\end{eqnarray}
この動画を見る
\begin{eqnarray}
{\Large\boxed{3}} ある高校の生徒30人に対し、50m走のタイムを2回計測した。\\
左図(※動画参照)は1回目の計測結果を横軸に2回目の計測結果\\
を縦軸に取った散布図である。\\
(1)次の(\textrm{A})から(\textrm{F})のうち、1回目の計測結果の箱ひげ図\\
として適当なものは\boxed{\ \ ネ\ \ }であり、2回目の計測結果の箱ひげ図として\\
適当なものは\boxed{\ \ ノ\ \ }である。\\
(2)次の(\textrm{G})から(\textrm{L})のうち、1回目と2回目の計測結果の合計の\\
箱ひげ図として適切なものは\boxed{\ \ ハ\ \ }である。\\
(3)遅れてやってきた31人目の生徒の50m走のタイムを2回計測した\\
結果、1回目は20.0(秒)、2回目は10.0(秒)であった。各生徒の2回の\\
計測結果の合計を考え、最初の30人の生徒の平均値を\bar{ x_{31} },中央値を\\
m_{31}とする。\bar{ x_{30} }=17.0であることに注意すると、\\
\bar{ x_{31} }-\bar{ x_{30} }=\boxed{\ \ ヒ\ \ }である。一方、\\
m_{31}-m_{30}=\boxed{\ \ フ\ \ }である。\\
\end{eqnarray}
