単元:
#数学(中学生)#高校入試過去問(数学)#青山学院高等部
指導講師:
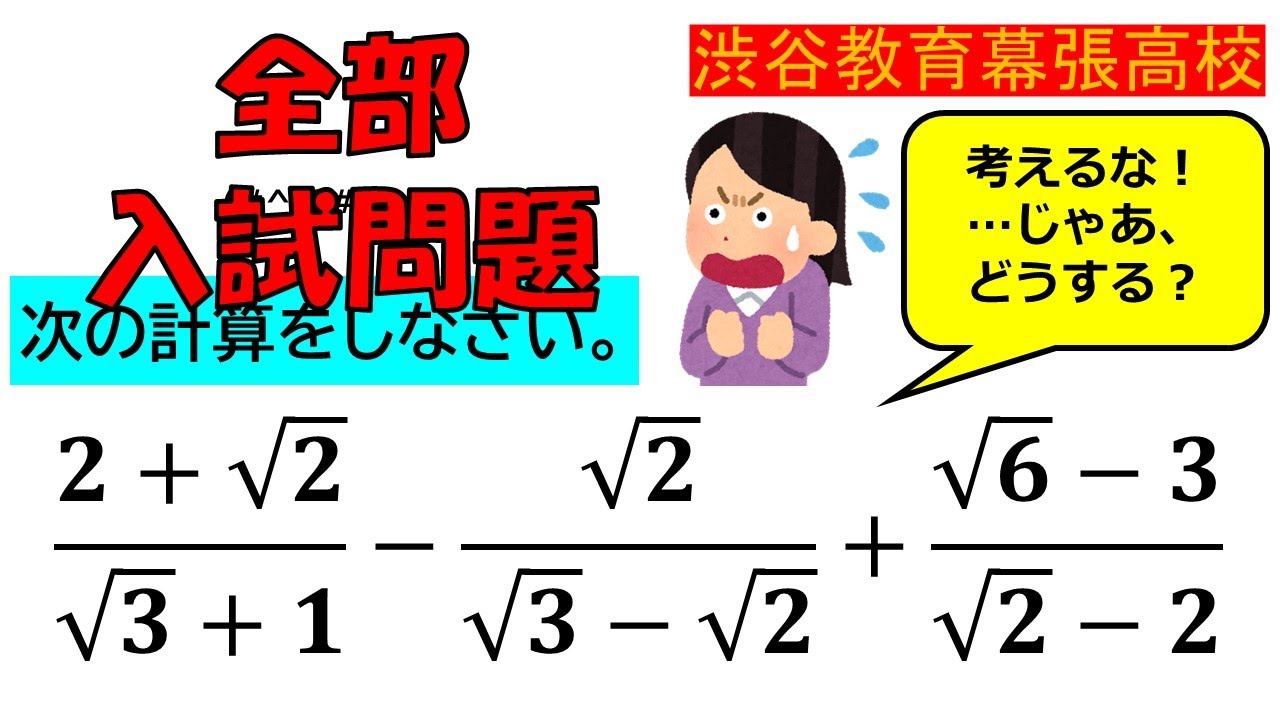
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
入試予想問題 青山学院高等部
星形$ABCDE$がある。
はじめに$A$の位置にコマを置き
さいころを$1$つ投げ、出た目の数 だけ移動する。
さいころを$2$回投げたとき、コマが 元の位置にある確率?
車で$50km$離れた$2$地点の間を往復した。
行きは$20$分間渋滞に巻き込まれ、
ガソリンを$3.66L$消費した。
帰りは$70$分間渋滞に巻き込まれ、
ガソリンを$4.06L$消費した。
この車は渋滞に巻き込まれていない時には$1km$進むのに$xmL$ガソリン消費。
渋滞中は$ymL$消費、渋滞中の車の速さは$100m$/分
$x, y =?$
2つの円が$A,B$で交わる。
また、 $P,C,D,E,F$は
$PE = 5 EB = 3 BF = 12 , DF=12,FDP = 90^{ \circ }$
(1)$DP =?$
(2)$AB =?$
(3)$\triangle AEF$の面積?
(4)$\triangle AEF$と$\triangle BDC$の 重った部の面積?
※図は動画内参照
平行四辺形$ABCD AB=3cm, AD=5cm CE=2cm$、各点は図のとおり
(1)$DF=?$
(2)$GE: EF = ?$
(3)$\Box AGED$と$\triangle BCG$の面積比?
※図は動画内参照
この動画を見る