ゆる言語学者 水野さん参上 - 質問解決D.B.（データベース）
Generic selectors
完全一致検索
タイトルから検索
記事本文から検索
Post Type Selectors
all_unit_post
質問解決D.B.（データベース） > 動画投稿 > 数学(高校生) > 数Ⅰ > 数と式 > 式の計算（整式・展開・因数分解） > ゆる言語学者　水野さん参上

ゆる言語学者　水野さん参上

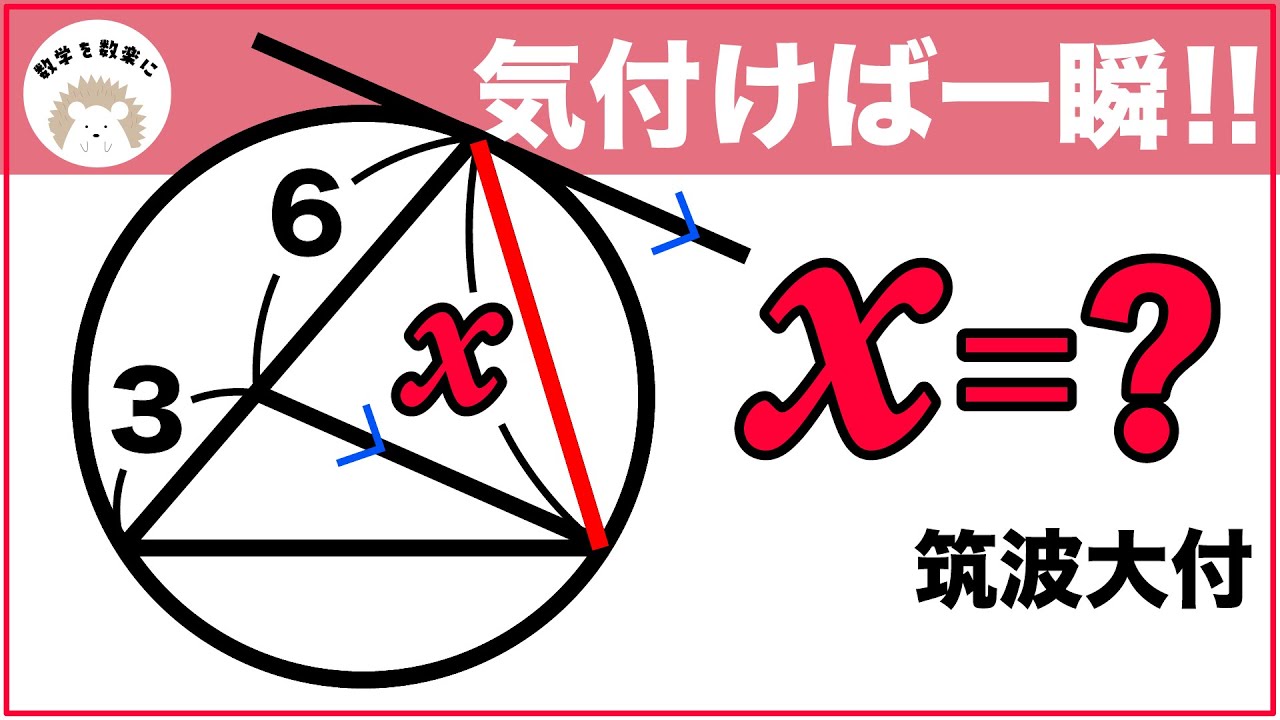
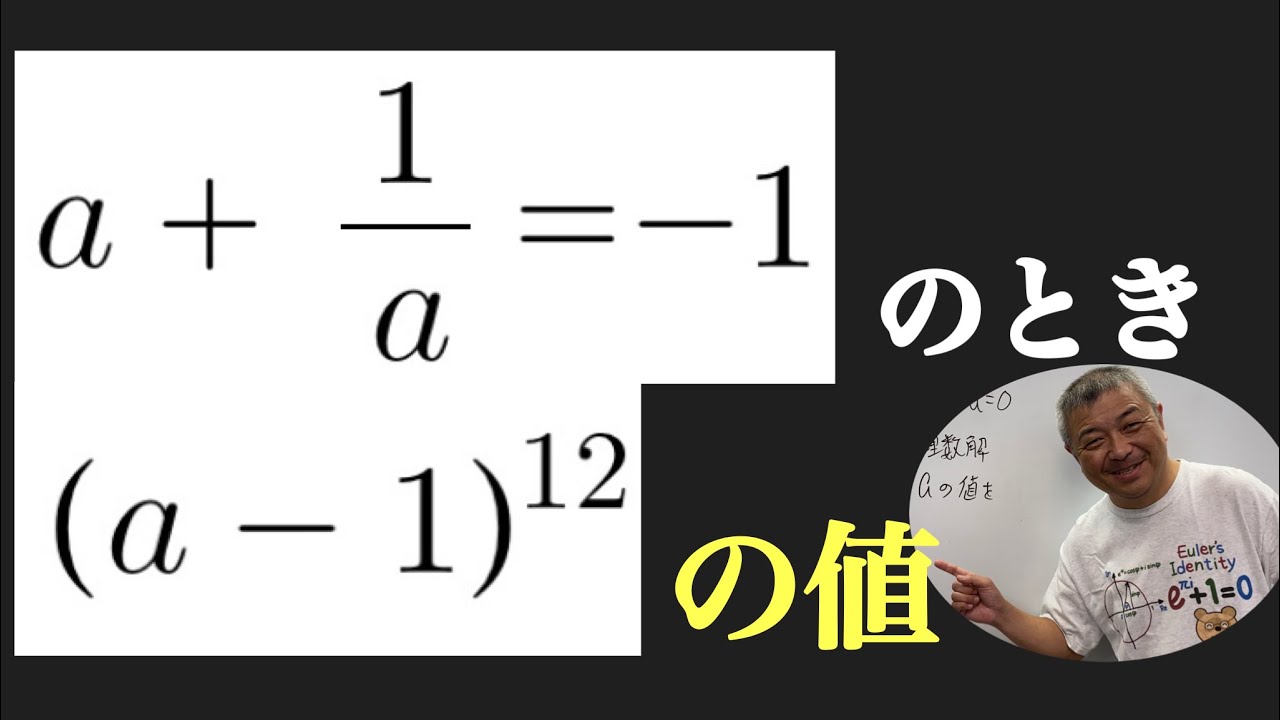問題文全文(内容文)：
定義域に関して解説していきます.
単元： #数Ⅰ#数と式#式の計算（整式・展開・因数分解）#数学(高校生)
指導講師： 鈴木貫太郎
問題文全文(内容文)：
定義域に関して解説していきます.
投稿日：2021.08.14

＜関連動画＞

「二次不等式の解の条件①」【高校数学ⅠA】を宇宙一わかりやすく

アイキャッチ画像
単元： #数Ⅰ#２次関数#2次方程式と2次不等式#数学(高校生)
指導講師： ハクシ高校【数学科】良問演習チャンネル
問題文全文(内容文)：
次の問いに答えよ。
（1）すべての実数$x$について、2次不等式$x^2-2kx-3k+4 \gt 0$が成り立つような$k$の値の範囲を求めよ。
（2）すべての実数$x$について、不等式$(k-2)x^2-2(k-I)x+3k-5 \geqq 0$が成り立つような$k$の値の範囲を求めよ。
この動画を見る　

【有名問題】京都大学の伝説の問題です【数学 入試問題】

アイキャッチ画像
単元： #数Ⅰ#大学入試過去問(数学)#数と式#実数と平方根（循環小数・有理数・無理数・絶対値・平方根計算・2重根号）#集合と命題（集合・命題と条件・背理法）#三角関数#加法定理とその応用#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)
指導講師： 数学・算数の楽しさを思い出した / Ken
問題文全文(内容文)：
$ tan1°$は有理数か？

数学入試問題過去問
この動画を見る　

富山大（医）　無理数の証明

アイキャッチ画像
単元： #数Ⅰ#数と式#実数と平方根（循環小数・有理数・無理数・絶対値・平方根計算・2重根号）#数学(高校生)
指導講師： 鈴木貫太郎
問題文全文(内容文)：
$p,q$は異なる素数であり,$k,m,n$は整数である.
$k+m\sqrt p+n\sqrt q=0$なら,$k=m=n=0$を示せ.

(1)$\sqrt p$が無理数であることを示せ.

2016富山大(医)
この動画を見る　

智弁和歌山2021 A

アイキャッチ画像
単元： #数学(中学生)#数Ⅰ#図形と計量#三角比（三角比・拡張・相互関係・単位円）#高校入試過去問(数学)#数学(高校生)
指導講師： 数学を数楽に
問題文全文(内容文)：
AB=5,BC=3,AE=?
＊図は動画内参照

2021智辯学園和歌山高等学校
この動画を見る　

【短時間でマスター!!】四分位数・四分位範囲・四分位偏差の求め方を解説！〔現役塾講師解説、数学〕

アイキャッチ画像
単元： #数Ⅰ#データの分析#データの分析#数学(高校生)
指導講師： 3rd School
問題文全文(内容文)：
数学1A
四分位数・四分位範囲・四分位偏差の求め方を解説します。
この動画を見る　
PAGE TOP