問題文全文(内容文):
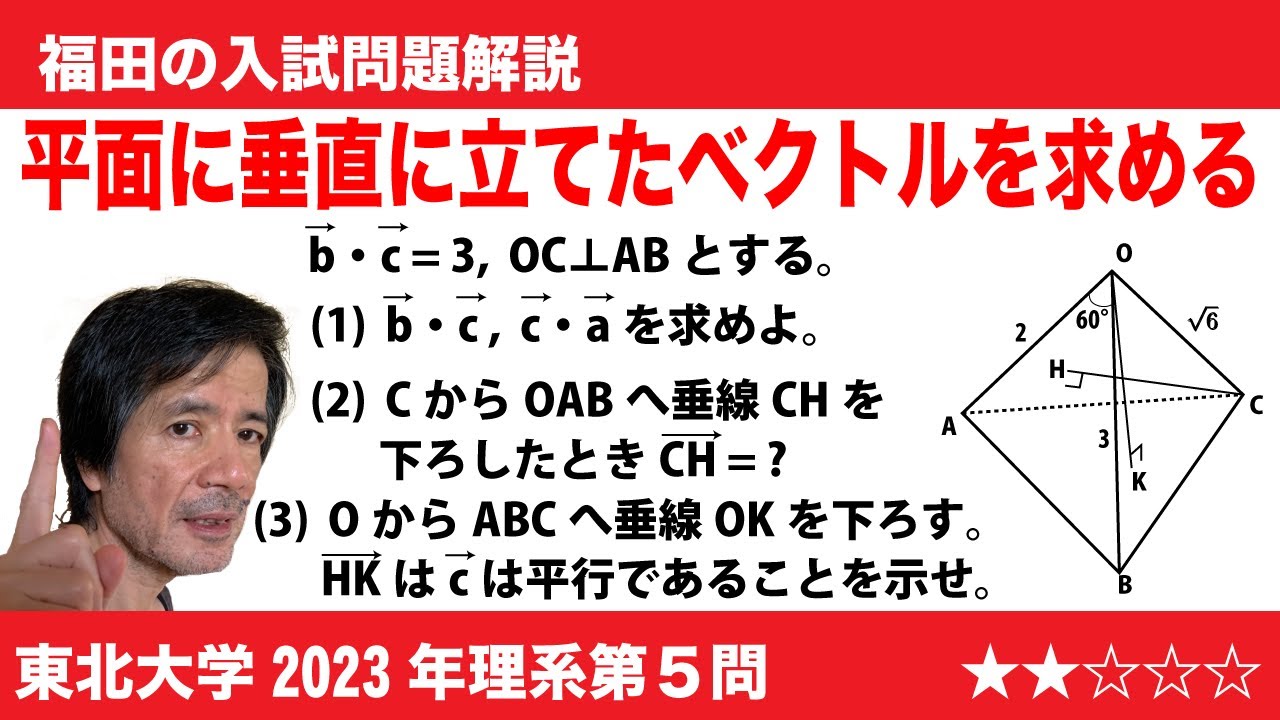
四面体OABCは,OA=4,OB=5,OC=3,∠AOB=90°,∠AOC=∠BOC=60°を満たしている。
(1)点Cから△OABに下した垂線と△OABとの交点をHとする。ベクトルCHをOA,OB,OCを用いて表そう。
(2)四面体OABCの体積を求めよう。
四面体OABCは,OA=4,OB=5,OC=3,∠AOB=90°,∠AOC=∠BOC=60°を満たしている。
(1)点Cから△OABに下した垂線と△OABとの交点をHとする。ベクトルCHをOA,OB,OCを用いて表そう。
(2)四面体OABCの体積を求めよう。
チャプター:
0:00 オープニング
0:05 問題文
0:20 問題解説(1)
3:43 問題解説(2)
4:49 別解(図形を座標に乗せる)
7:35 名言
単元:
#大学入試過去問(数学)#空間ベクトル#空間ベクトル#学校別大学入試過去問解説(数学)#東京理科大学#数学(高校生)#数C
指導講師:
理数個別チャンネル
問題文全文(内容文):
四面体OABCは,OA=4,OB=5,OC=3,∠AOB=90°,∠AOC=∠BOC=60°を満たしている。
(1)点Cから△OABに下した垂線と△OABとの交点をHとする。ベクトルCHをOA,OB,OCを用いて表そう。
(2)四面体OABCの体積を求めよう。
四面体OABCは,OA=4,OB=5,OC=3,∠AOB=90°,∠AOC=∠BOC=60°を満たしている。
(1)点Cから△OABに下した垂線と△OABとの交点をHとする。ベクトルCHをOA,OB,OCを用いて表そう。
(2)四面体OABCの体積を求めよう。
投稿日:2021.01.17