【裏技】平行線と角度のこれ知ってた？

問題文全文(内容文)：
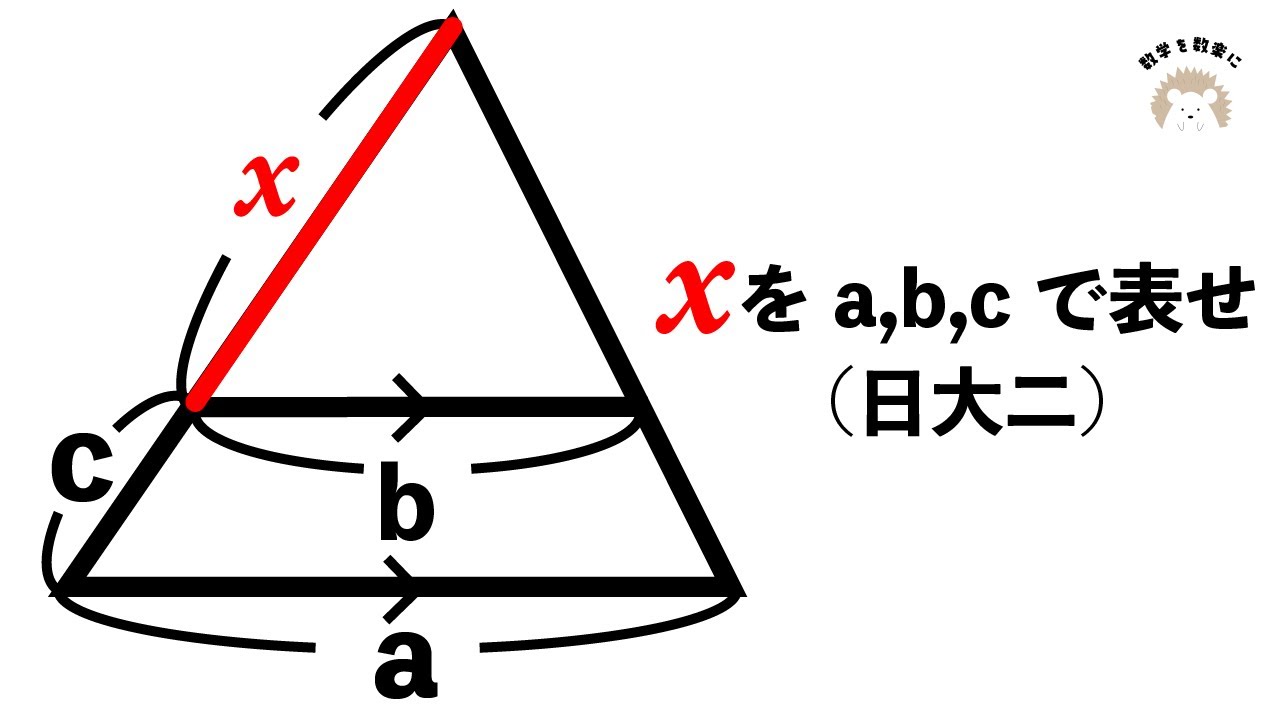
図は2本の平行な直線の間にZ型の線が引かれている。
※図は動画内参照
角xを求めよ。

単元： #数学(中学生)#中２数学#平行と合同

指導講師：【楽しい授業動画】あきとんとん

問題文全文(内容文)：
図は2本の平行な直線の間にZ型の線が引かれている。
※図は動画内参照
角xを求めよ。

投稿日：2022.10.26

単元： #数学(中学生)#中２数学#平面図形#角度と面積#図形の移動#平面図形その他#三角形と四角形

指導講師：いつもの先生

問題文全文(内容文)：
正三角形を図のように折り返したとき、
色のついた部分の面積は？

＊図は動画内参照

この動画を見る　

単元： #算数(中学受験)#数学(中学生)#中２数学#連立方程式#速さ#速さその他

指導講師：いつもの先生

問題文全文(内容文)：
家から池の前を通って、1400m離れた駅まで行くのに、
家から池までは分速60m、
池から駅までは分速50mで歩くと、
全体で26分かかりました。
家から池まで、池から駅までの道のりを、
それぞれ求めなさい。

この動画を見る　

単元： #数学(中学生)#中２数学#三角形と四角形

指導講師：数学を数楽に

問題文全文(内容文)：
△ABC=?
＊図は動画内参照

この動画を見る　

単元： #数学(中学生)#中２数学#確率#福岡県公立高等学校

指導講師：高校入試から見た数学の世界「全部入試問題」by しろたん

問題文全文(内容文)：
4枚の硬貨A、B、C、Dを同時に投げる。少なくとも1枚は表が出る確率を求めよ。硬貨のそれぞれについて、表と裏の出ることは同様に確からしいとする。

この動画を見る　

単元： #数学(中学生)#中２数学#平行と合同

指導講師：中学受験算数・高校受験数学けいたくチャンネル

問題文全文(内容文)：
中2～合同な図形～

例題次の図の2つの四角形は合同です。

(1) 2つの四角形が合同であることを記号≡を使って表しなさい。

(2) 次の辺の長さや角の大きさを求めなさい。
① 辺EH ② 辺DC ③ ∠A

※図は動画内参照

この動画を見る　