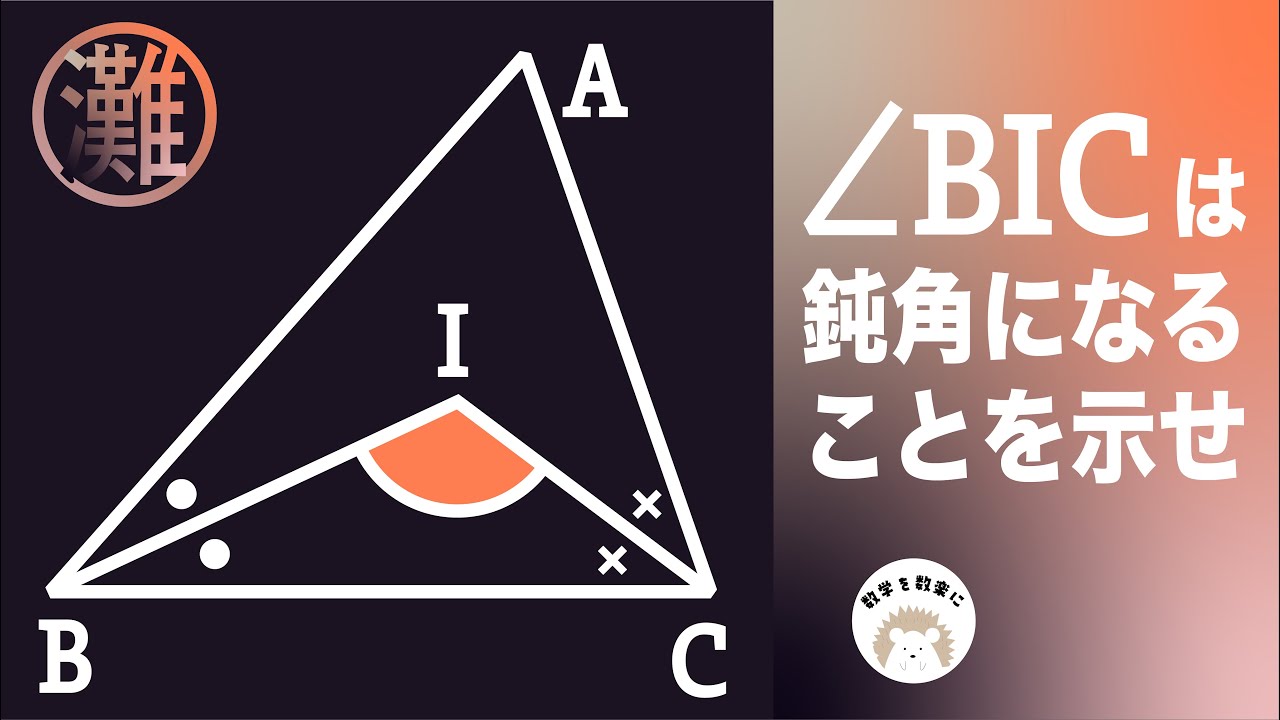
問題文全文(内容文):
右の図は,$ AB = 3cm,BC = 2cm,\angle ABC = 90°$の
直角三角形$ABC$を底面とし,
点$D$を頂点とする三角錐であり,
$AD=6cm,\angle ABD= \angle CBD = 90°$である.
また,点$E$は辺$AD$上の点で,$AE = 2cm$である.
このとき,次の各問いに答えなさい.
①この三角錐の体積を求めなさい.
②この三角錐の表面に,点$C$から辺$BD$を通るように,
点$E$まで細い糸をかける.
かけた糸の長さが最も短くなるとき,その糸の長さを求めなさい.
ただし糸はのびたり縮んだりしないものとする.
図は動画内参照
右の図は,$ AB = 3cm,BC = 2cm,\angle ABC = 90°$の
直角三角形$ABC$を底面とし,
点$D$を頂点とする三角錐であり,
$AD=6cm,\angle ABD= \angle CBD = 90°$である.
また,点$E$は辺$AD$上の点で,$AE = 2cm$である.
このとき,次の各問いに答えなさい.
①この三角錐の体積を求めなさい.
②この三角錐の表面に,点$C$から辺$BD$を通るように,
点$E$まで細い糸をかける.
かけた糸の長さが最も短くなるとき,その糸の長さを求めなさい.
ただし糸はのびたり縮んだりしないものとする.
図は動画内参照
単元:
#数学(中学生)#中1数学#空間図形
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
右の図は,$ AB = 3cm,BC = 2cm,\angle ABC = 90°$の
直角三角形$ABC$を底面とし,
点$D$を頂点とする三角錐であり,
$AD=6cm,\angle ABD= \angle CBD = 90°$である.
また,点$E$は辺$AD$上の点で,$AE = 2cm$である.
このとき,次の各問いに答えなさい.
①この三角錐の体積を求めなさい.
②この三角錐の表面に,点$C$から辺$BD$を通るように,
点$E$まで細い糸をかける.
かけた糸の長さが最も短くなるとき,その糸の長さを求めなさい.
ただし糸はのびたり縮んだりしないものとする.
図は動画内参照
右の図は,$ AB = 3cm,BC = 2cm,\angle ABC = 90°$の
直角三角形$ABC$を底面とし,
点$D$を頂点とする三角錐であり,
$AD=6cm,\angle ABD= \angle CBD = 90°$である.
また,点$E$は辺$AD$上の点で,$AE = 2cm$である.
このとき,次の各問いに答えなさい.
①この三角錐の体積を求めなさい.
②この三角錐の表面に,点$C$から辺$BD$を通るように,
点$E$まで細い糸をかける.
かけた糸の長さが最も短くなるとき,その糸の長さを求めなさい.
ただし糸はのびたり縮んだりしないものとする.
図は動画内参照
投稿日:2016.08.15