【とにかく、解け！】図形：静岡県高校入試～全国入試問題解法 - 質問解決D.B.（データベース）
Generic selectors
完全一致検索
タイトルから検索
記事本文から検索
Post Type Selectors
all_unit_post
質問解決D.B.（データベース） > 動画投稿 > 数学(中学生) > 高校入試過去問(数学) > 静岡県公立高校入試 > 【とにかく、解け！】図形：静岡県高校入試～全国入試問題解法

【とにかく、解け！】図形：静岡県高校入試～全国入試問題解法

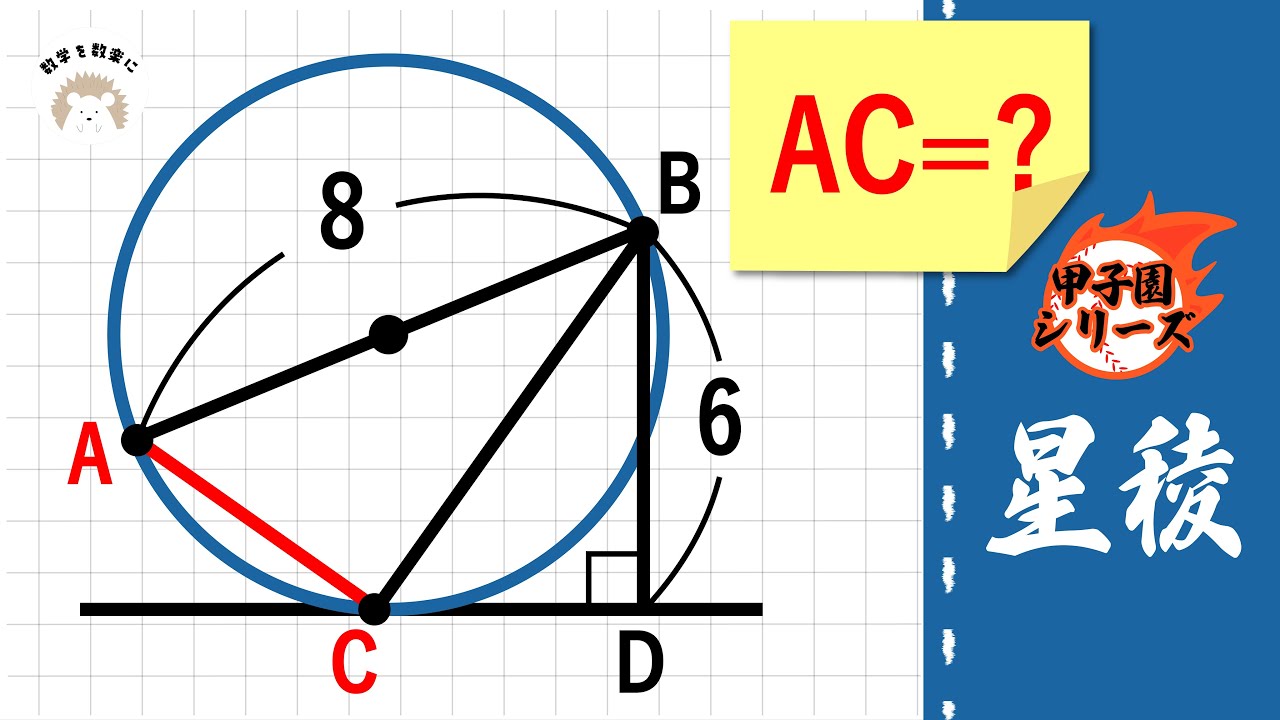
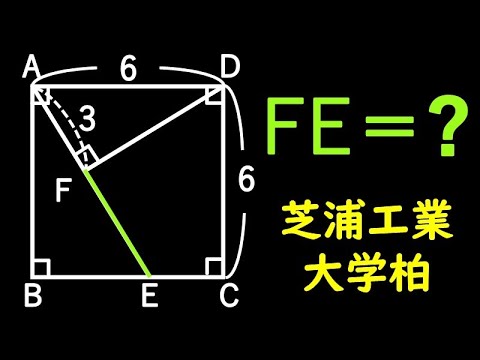
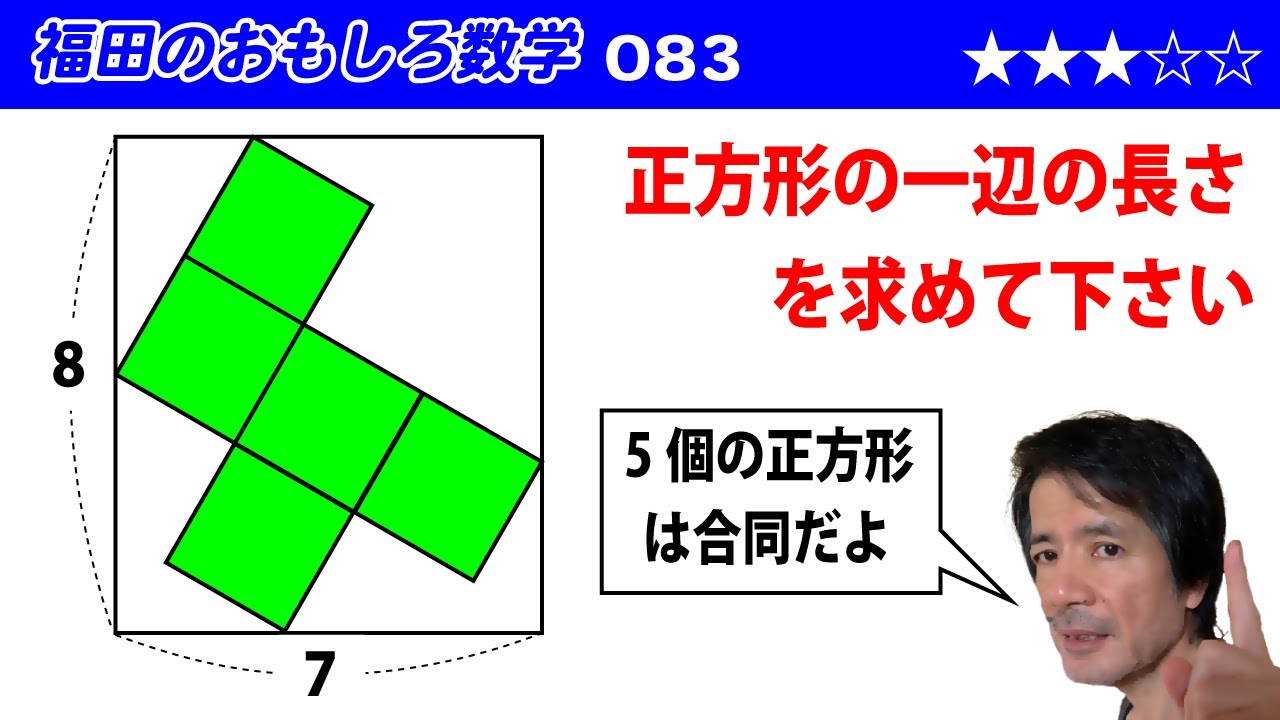
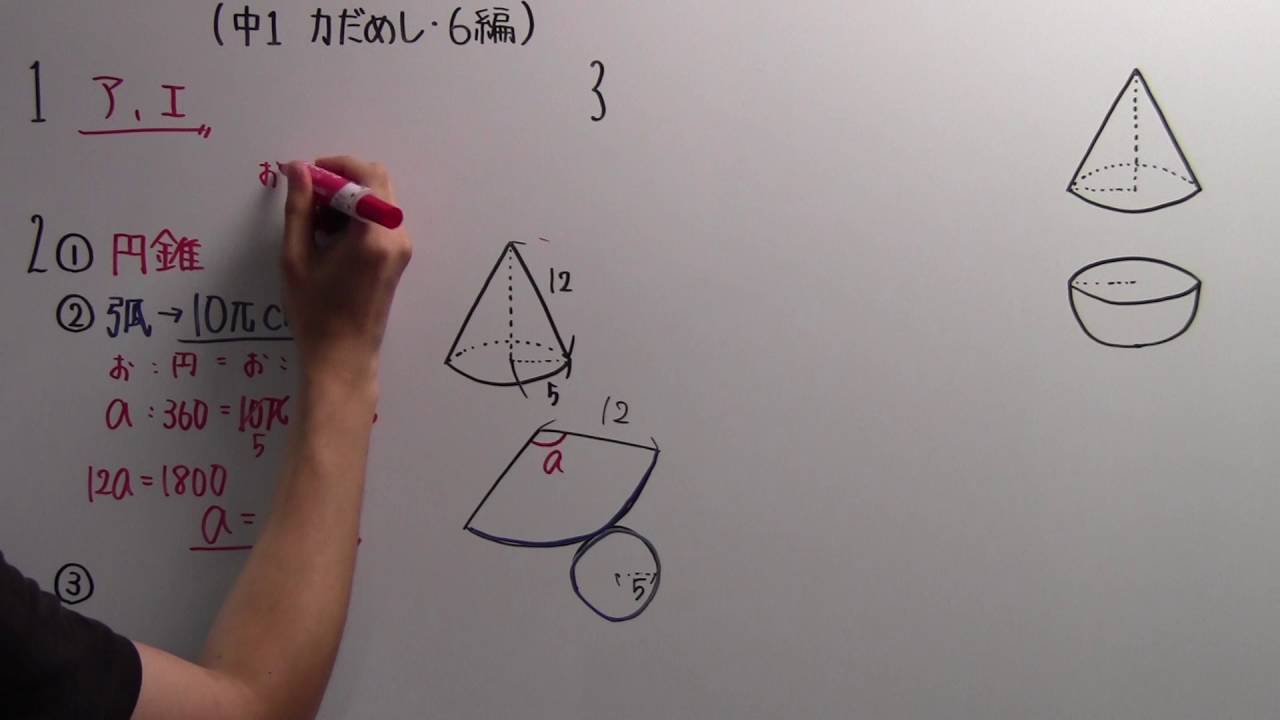問題文全文(内容文)：
入試問題　静岡県の高校

円すいの展開図:
底面→半径$2cm$の円
側面→半径$5cm$の扇形
このおうぎ型の中心角の 大きさを求めなさい。
※図は動画内参照
単元： #数学(中学生)#空間図形#平面図形#静岡県公立高校入試
指導講師： 高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文)：
入試問題　静岡県の高校

円すいの展開図:
底面→半径$2cm$の円
側面→半径$5cm$の扇形
このおうぎ型の中心角の 大きさを求めなさい。
※図は動画内参照
投稿日：2020.11.06

＜関連動画＞

PAGE TOP