中学受験算数「倍数と公倍数③」小学４年生～６年生対象【毎日配信】 - 質問解決D.B.（データベース）
Generic selectors
完全一致検索
タイトルから検索
記事本文から検索
Post Type Selectors
all_unit_post
質問解決D.B.（データベース） > 動画投稿 > 算数(中学受験) > 計算と数の性質 > 約数・倍数を利用する問題 > 中学受験算数「倍数と公倍数③」小学４年生～６年生対象【毎日配信】

中学受験算数「倍数と公倍数③」小学４年生～６年生対象【毎日配信】

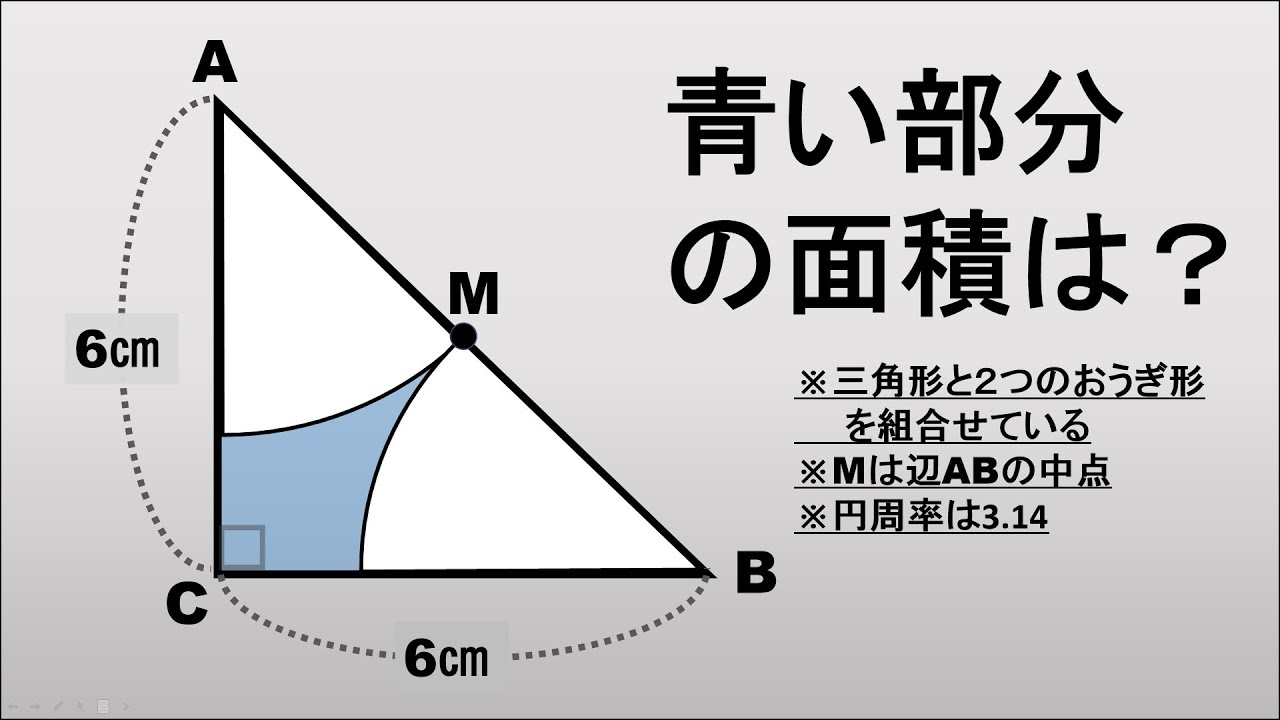
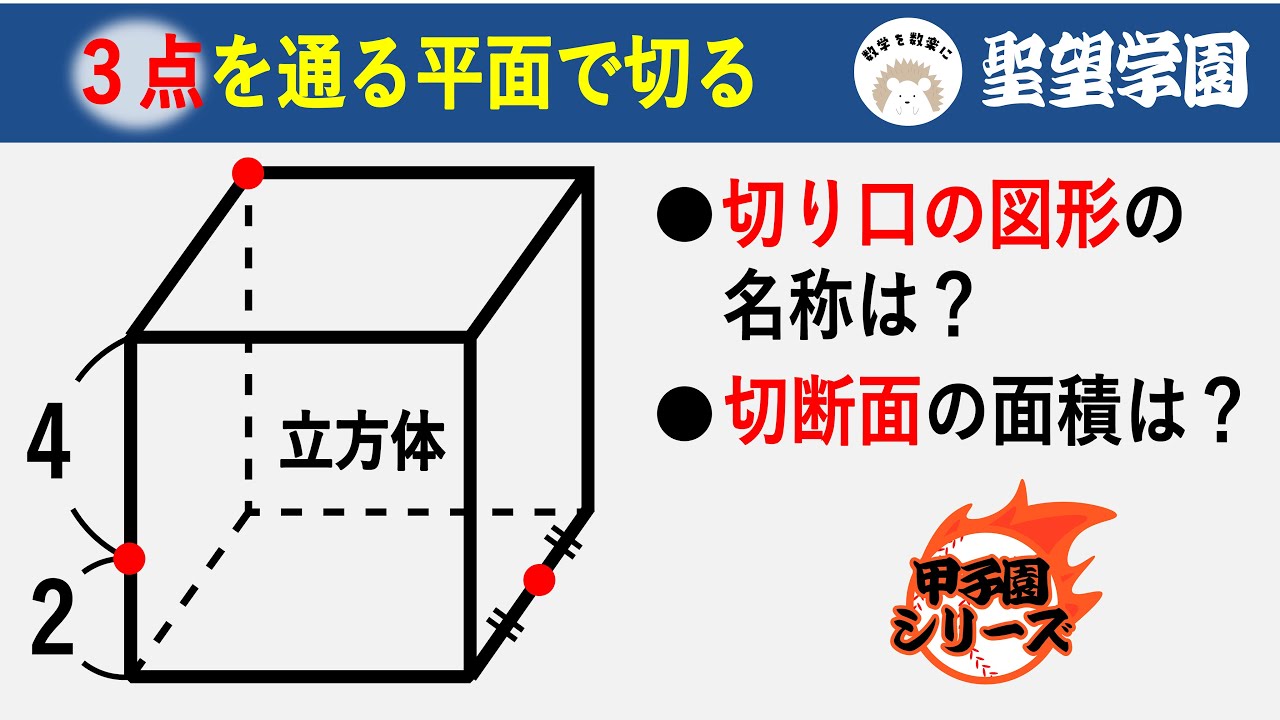
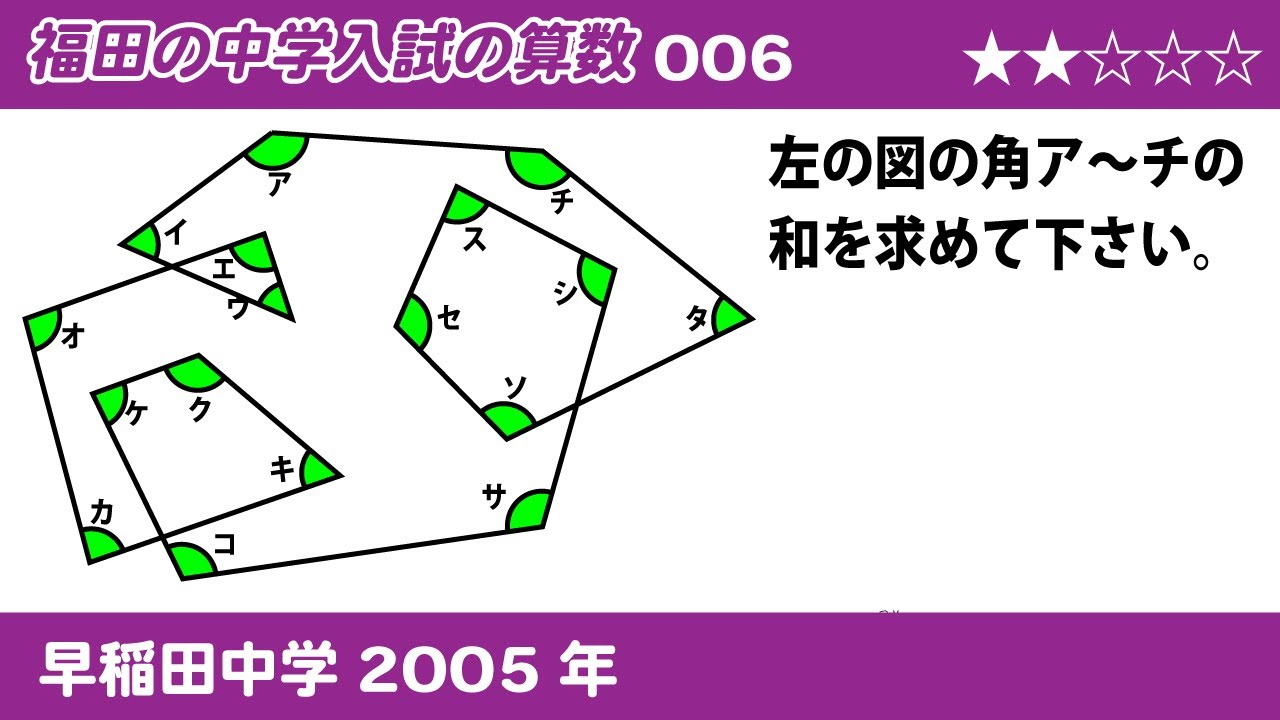
問題文全文(内容文)：
第19回倍数と公倍数③

例1
3けたの整数21が3の倍数であるとき、口にあてはまる 数をすべて求めなさい。

例2
1から100までの整数の中に、3でも4でもわり切れない数は いくつありますか。
単元： #算数(中学受験)#計算と数の性質#約数・倍数を利用する問題
指導講師： 中学受験算数・高校受験数学けいたくチャンネル
問題文全文(内容文)：
第19回倍数と公倍数③

例1
3けたの整数21が3の倍数であるとき、口にあてはまる 数をすべて求めなさい。

例2
1から100までの整数の中に、3でも4でもわり切れない数は いくつありますか。
投稿日：2020.04.19

＜関連動画＞

【中学受験問題に挑戦】46　（”大人”は頭の体操）7つの円の面積問題

アイキャッチ画像
単元： #算数(中学受験)#平面図形#角度と面積
指導講師： 算数・数学ちゃんねる
問題文全文(内容文)：
7つの円の世界の面積問題を解説していきます。
オレンジ色の部分の面積は？
この動画を見る　

ポイントは２組の○○！？定番の解き方だけで解けます！【中学受験算数】【入試問題】【灘中学校】

アイキャッチ画像
単元： #算数(中学受験)#平面図形#角度と面積
指導講師： こばちゃん塾
問題文全文(内容文)：
2023年　灘中学校
下図の四角形EFGHの面積は？
＊図は動画内参照
この動画を見る　

25%引きって答えたら、巣鴨中落ちるよ！　2025年巣鴨中　#中学受験 #算数 #割合

アイキャッチ画像
単元： #算数(中学受験)#過去問解説(学校別)#文章題#単位・比と割合・比例・反比例#巣鴨中学
指導講師： 重吉
問題文全文(内容文)：
ある品物に25％の利益をみこんで定価をつけました。さらに定価の(　　)％引きで売ったところ、利益も損もありませんでした。(　　)に当てはまる数を答えなさい。
この動画を見る　

灘中　ちょっと合同式

アイキャッチ画像
単元： #算数(中学受験)#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#過去問解説(学校別)#数学(高校生)#灘中学校
指導講師： 鈴木貫太郎
問題文全文(内容文)：
連続した5つの整数の積が2441880　最初の整数は？

出典：2002年灘中学校　過去問
この動画を見る　

【テスト対策・中１】２章－２

アイキャッチ画像
単元： #文章題#文章題その他
指導講師： とある男が授業をしてみた
問題文全文(内容文)：
次の数量の関係を,等式か不等式に表しなさい.

①あめを1人7個ずつ$a$人に配ると,60個ではたりない.

②1000円で,$x$円の品物を3個と$y$円の品物を1個買うことができた.

③兄は0円,弟は$b$円持っていたが,兄が弟に$C$円渡したので,
2人の所持金が同じになった.

④底辺の長さが$6cm$,高さが$xcm$の三角形の面積は$ycm^2$以下である。
この動画を見る　
Back to top