一次方程式の解法を知る15秒！～全国入試問題解法 #shorts #数学 #高校入試 #動体視力

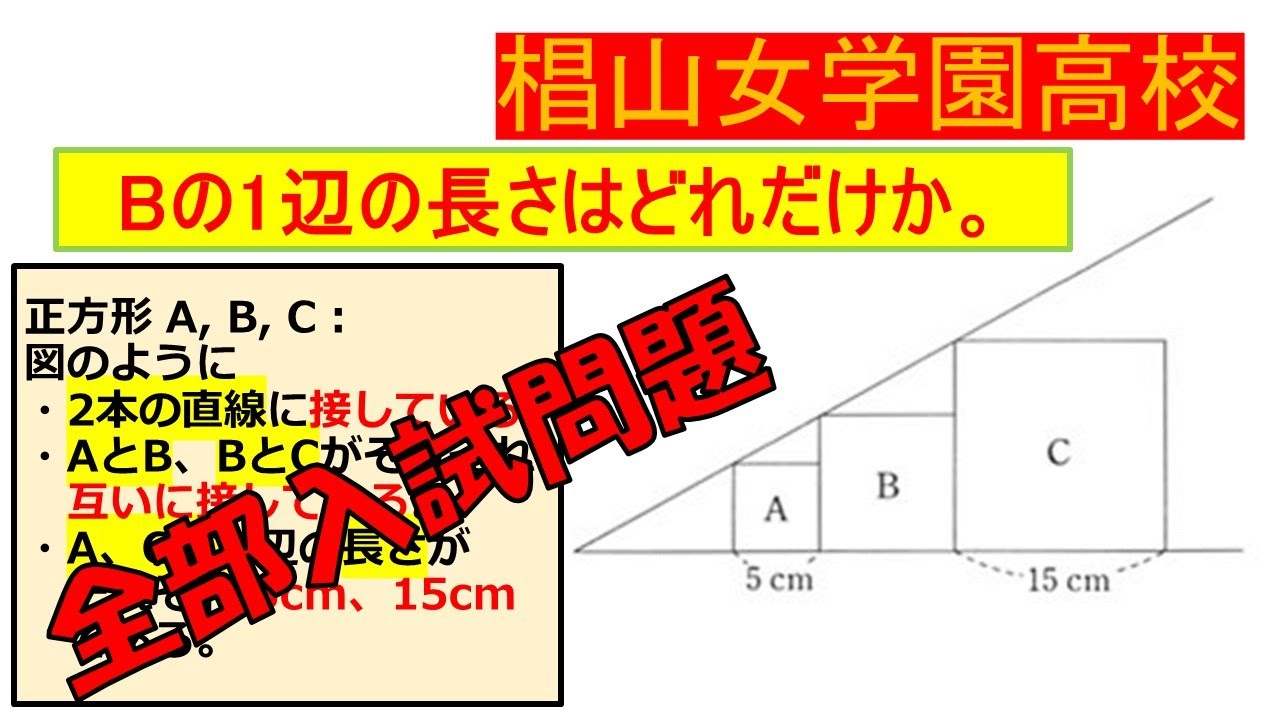
問題文全文(内容文)：
方程式$ 3-\dfrac{x-5}{12}=0.25(3x+2)$を解け.

関西大倉高校過去問

単元： #数学(中学生)#中１数学#方程式

指導講師：高校入試から見た数学の世界「全部入試問題」by しろたん

問題文全文(内容文)：
方程式$ 3-\dfrac{x-5}{12}=0.25(3x+2)$を解け.

関西大倉高校過去問

投稿日：2023.09.23

＜関連動画＞

中１数学「比例のグラフの書き方」【毎日配信】

単元： #数学(中学生)#中１数学#比例・反比例

指導講師：中学受験算数・高校受験数学けいたくチャンネル

問題文全文(内容文)：
比例のグラフの書き方に関して解説していきます。

この動画を見る　

手を動かすだけの問題

単元： #方程式#数と式

指導講師：鈴木貫太郎

問題文全文(内容文)：
$ \dfrac{1}{x}-\dfrac{1}{2y}=\dfrac{1}{2x+y}$のとき,
$\dfrac{y^2}{x^2}+\dfrac{x^2}{y^2}$の値を求めよ.

シンガポール数学オリンピック過去問

この動画を見る　

【中1 数学】中1-37 方程式の利用⑤ 追いつく編

単元： #数学(中学生)#中１数学#方程式

指導講師：とある男が授業をしてみた

問題文全文(内容文)：
みはじの問題は①＿＿を書こう！

◎兄が1800m離れたコンビニに向かって家を出発した。
それから10分後に、妹が兄が忘れた財布を持って、自転車で同じ道を追いかけた。
兄は分速90m、妹は分速270mで進むとする。

②妹が出発してから何分後に追いつく？

③家から何m離れたところで追いつく？

④もし妹が16分後に家を出たとしたら、兄がコンビニに着くまでに追いつける？
(理由も答えてね！)

この動画を見る　

【中１　数学】　　１－２（旧）　加法・減法

単元： #数学(中学生)#中１数学#正の数・負の数

指導講師：とある男が授業をしてみた

問題文全文(内容文)：
加法、減法の計算問題
$(+4)+(+5)=$
$(+4)+(-5)=$
$(+9)-(-3)=$
を求めよ。

この動画を見る　

【中学数学】文字のかけ算・割り算～計算のテクニック～ 2-4【中１数学】

単元： #数学(中学生)#中１数学#文字と式

指導講師：【楽しい授業動画】あきとんとん

この動画を見る　

<img src="https://kaiketsu-db.net/wp-content/uploads/2021/11/112-book-morph-outline.gif" alt="" data-eio="l"> 一次方程式の解法を知る15秒！～全国入試問題解法 #shorts #数学 #高校入試 #動体視力

＜関連動画＞

中１数学「比例のグラフの書き方」【毎日配信】

手を動かすだけの問題

【中1 数学】中1-37 方程式の利用⑤ 追いつく編

【中１ 数学】 １－２（旧） 加法・減法

【中学数学】文字のかけ算・割り算～計算のテクニック～ 2-4【中１数学】

一次方程式の解法を知る15秒！～全国入試問題解法 #shorts #数学 #高校入試 #動体視力

【中１　数学】　　１－２（旧）　加法・減法