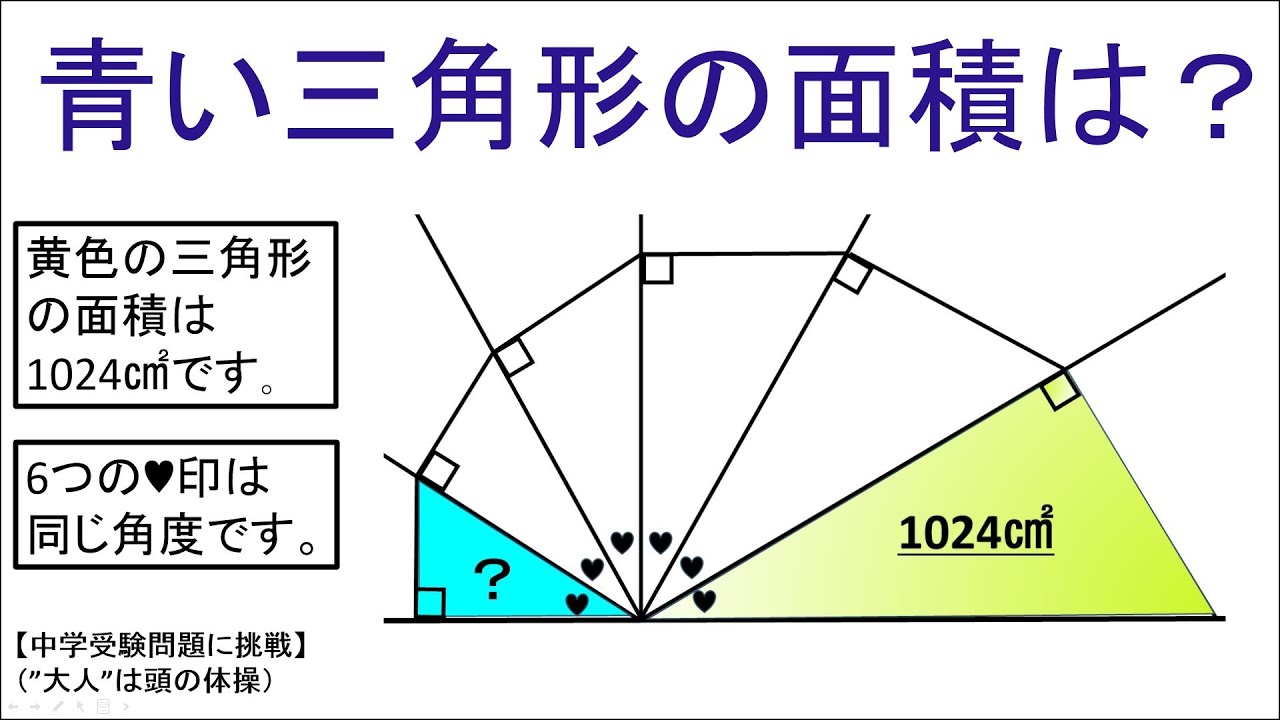
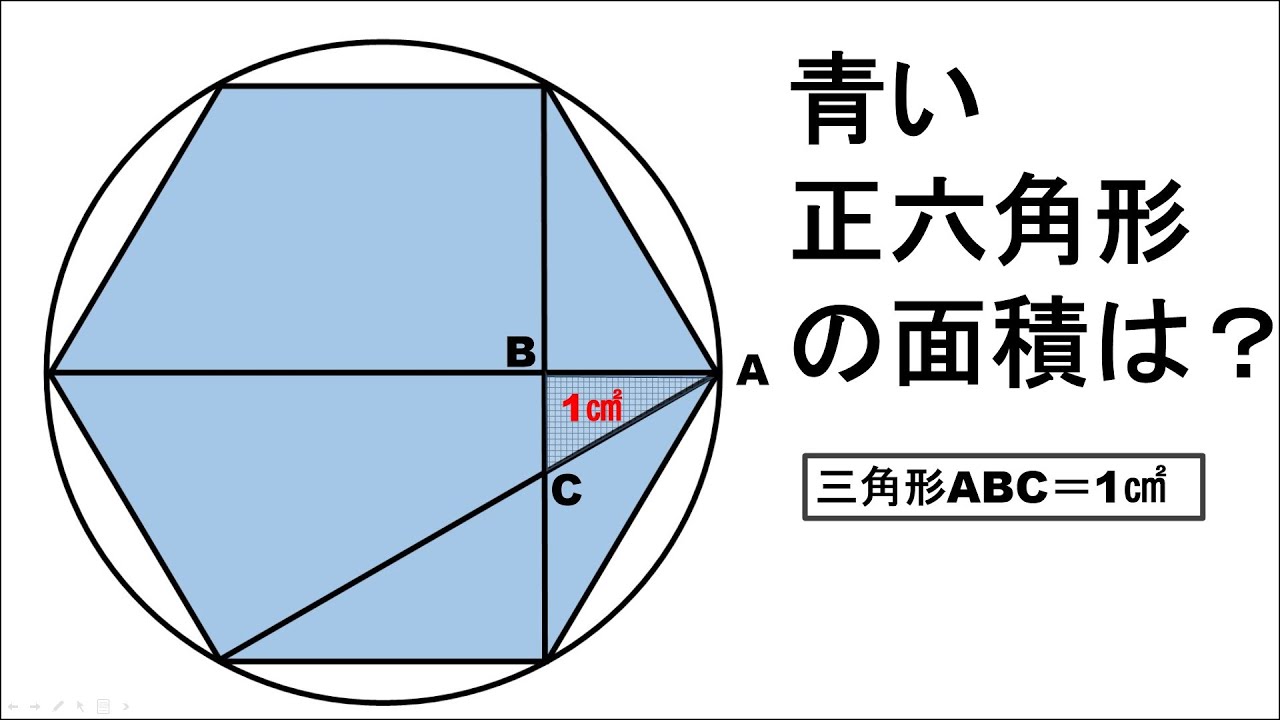
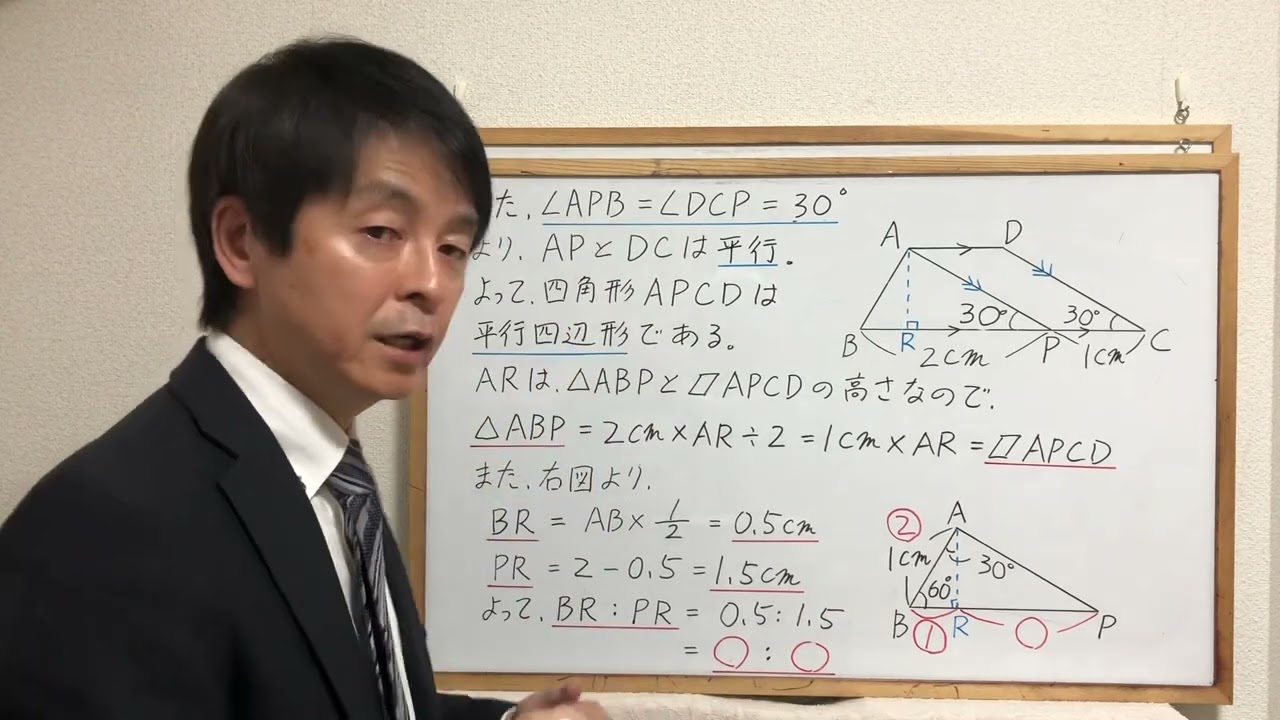
問題文全文(内容文):
4つの異なる整数A,B,C,Dがあります。
これらの整数のうち異なる2つをたすと全部で6つの数ができますが、この6つの数の中に同じ数があったので、できた数は10,13,15,17,20の5種類でした。
4つの整数A,B,C,Dの積を求めなさい。
出典:2024年立教新座中学校 入試問題
4つの異なる整数A,B,C,Dがあります。
これらの整数のうち異なる2つをたすと全部で6つの数ができますが、この6つの数の中に同じ数があったので、できた数は10,13,15,17,20の5種類でした。
4つの整数A,B,C,Dの積を求めなさい。
出典:2024年立教新座中学校 入試問題
単元:
#算数(中学受験)#過去問解説(学校別)#文章題#和差算・植木算・分配算・倍数算・年齢算・相当算・つるかめ算#立教新座中学
指導講師:
重吉
問題文全文(内容文):
4つの異なる整数A,B,C,Dがあります。
これらの整数のうち異なる2つをたすと全部で6つの数ができますが、この6つの数の中に同じ数があったので、できた数は10,13,15,17,20の5種類でした。
4つの整数A,B,C,Dの積を求めなさい。
出典:2024年立教新座中学校 入試問題
4つの異なる整数A,B,C,Dがあります。
これらの整数のうち異なる2つをたすと全部で6つの数ができますが、この6つの数の中に同じ数があったので、できた数は10,13,15,17,20の5種類でした。
4つの整数A,B,C,Dの積を求めなさい。
出典:2024年立教新座中学校 入試問題
投稿日:2024.07.09