中学受験類題45 角Xは何度？（おうぎ形の面積＝円の面積） - 質問解決D.B.（データベース）
Generic selectors
完全一致検索
タイトルから検索
記事本文から検索
Post Type Selectors
all_unit_post
質問解決D.B.（データベース） > 動画投稿 > 算数(中学受験) > 平面図形 > 角度と面積 > 中学受験類題45　角Xは何度？（おうぎ形の面積＝円の面積）

中学受験類題45　角Xは何度？（おうぎ形の面積＝円の面積）

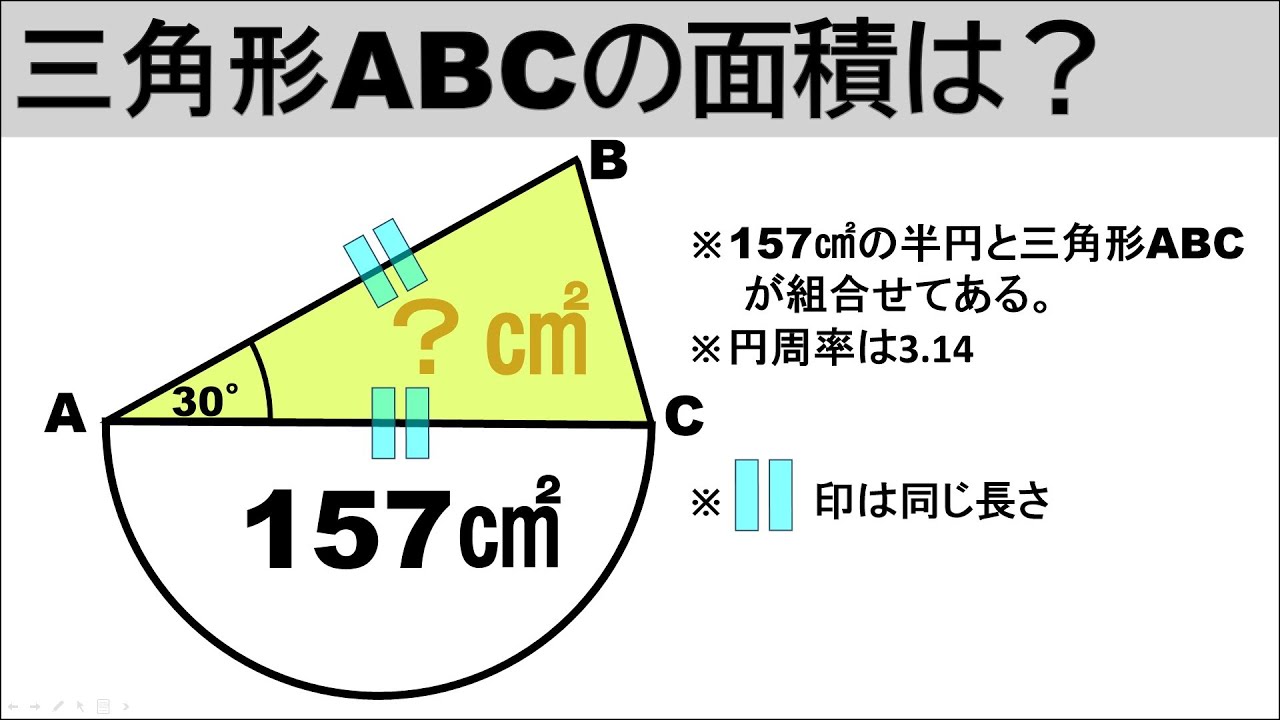
問題文全文(内容文)：
面積問題からの角度問題を解説していきます。
扇形と円が等しいときの角Ｘは何度か？
単元： #算数(中学受験)#平面図形#角度と面積
指導講師： 【楽しい授業動画】あきとんとん
問題文全文(内容文)：
面積問題からの角度問題を解説していきます。
扇形と円が等しいときの角Ｘは何度か？
投稿日：2023.08.19

＜関連動画＞

【受験算数】規則性に関する問題：（練習❸）三角数と群数列【予習シリーズ演習問題集・小5下】

アイキャッチ画像
単元： #算数(中学受験)#計算と数の性質#規則性（周期算・方陣算・数列・日暦算・N進法）
教材： #予習シ#予習シ演問・小5下#中学受験教材#規則性に関する問題
指導講師： 理数個別チャンネル
問題文全文(内容文)：
右の図のように、1から順に整数を並べていきます。これについて、次の問いに答えなさい。
(1)1段目の8列目の数はいくつですか。また、8段目の1列目の数はいくつですか。
(2)99は何段目の何列目の数ですか。
(3)10段目の5列目の数はいくつですか。
この動画を見る　

灘中　中学入試問題シリーズ　整数問題

アイキャッチ画像
単元： #算数(中学受験)#計算と数の性質#約数・倍数を利用する問題#過去問解説(学校別)#灘中学校
指導講師： 鈴木貫太郎
問題文全文(内容文)：
灘中学校過去問題
6桁の整数　5ABC15が999の倍数である。
ABCを求めよ。
この動画を見る　

【SPX小5算数51-24】仕事算(A5)：水を入れながら出す【D-支援確認編】

アイキャッチ画像
単元： #算数(中学受験)#文章題#仕事算とニュートン算
教材： #SPX#5年算数D-支援#中学受験教材
指導講師： 受験算数の森
問題文全文(内容文)：
ある水そうに、注水管Aを使うと28分で空の状態が満水になり、排水管Bを使うと12分で満水の状態が空になります。今、満水の状態の水そうに、A、B両管を同時に使うと何分で空になりますか。
この動画を見る　

定番過ぎる！解法テクニックがギュッと詰まった問題！補助線の場所がすぐに思いつく？【中学受験算数】【入試問題】【洗足学園中学校】

アイキャッチ画像
単元： #算数(中学受験)#過去問解説(学校別)#平面図形#角度と面積#洗足学園中学
指導講師： こばちゃん塾
問題文全文(内容文)：
・左図で、lとmが平行でABとACの長さが等しく、㋑が㋐の3倍の大きさの角度のとき、㋒は何度？

・左図の正六角形ABCDEFにおいて、角xは何度？

・左図のようなABを直径とする円があります。斜線部は何㎠？

＊図は動画内参照
この動画を見る　

ある条件を見逃すと一生解けない！？誰もが見逃しやすいその条件は○○【中学受験算数】【入試問題】【江戸川女子中学校】

アイキャッチ画像
単元： #算数(中学受験)#過去問解説(学校別)#平面図形#角度と面積#ラ・サール中学#桜蔭中学
指導講師： こばちゃん塾
問題文全文(内容文)：
2021城西川越中学校
下図のlとmは平行で、三角形ABCは正三角形です。
角㋐は何度？

2021桐蔭学園中等教育学校
下図の印がついた角の大きさの合計は何度？

2021ラ・サール中学校
下図で、ADとBCが平行、AE=BE、BC=BDです。
角㋐、角㋑は何度？

2021江戸川女子中学校
下図は正方形を折り返したところを表している。角㋐は何度？

＊図は動画内参照
この動画を見る　
PAGE TOP