【高校数学】独立な試行の確率～イメージでいけんじゃね？～ 2-5【数学A】 - 質問解決D.B.（データベース）
Generic selectors
完全一致検索
タイトルから検索
記事本文から検索
Post Type Selectors
all_unit_post
質問解決D.B.（データベース） > 動画投稿 > 数学(高校生) > 数A > 【高校数学】独立な試行の確率～イメージでいけんじゃね？～ 2-5【数学A】

【高校数学】独立な試行の確率～イメージでいけんじゃね？～ 2-5【数学A】

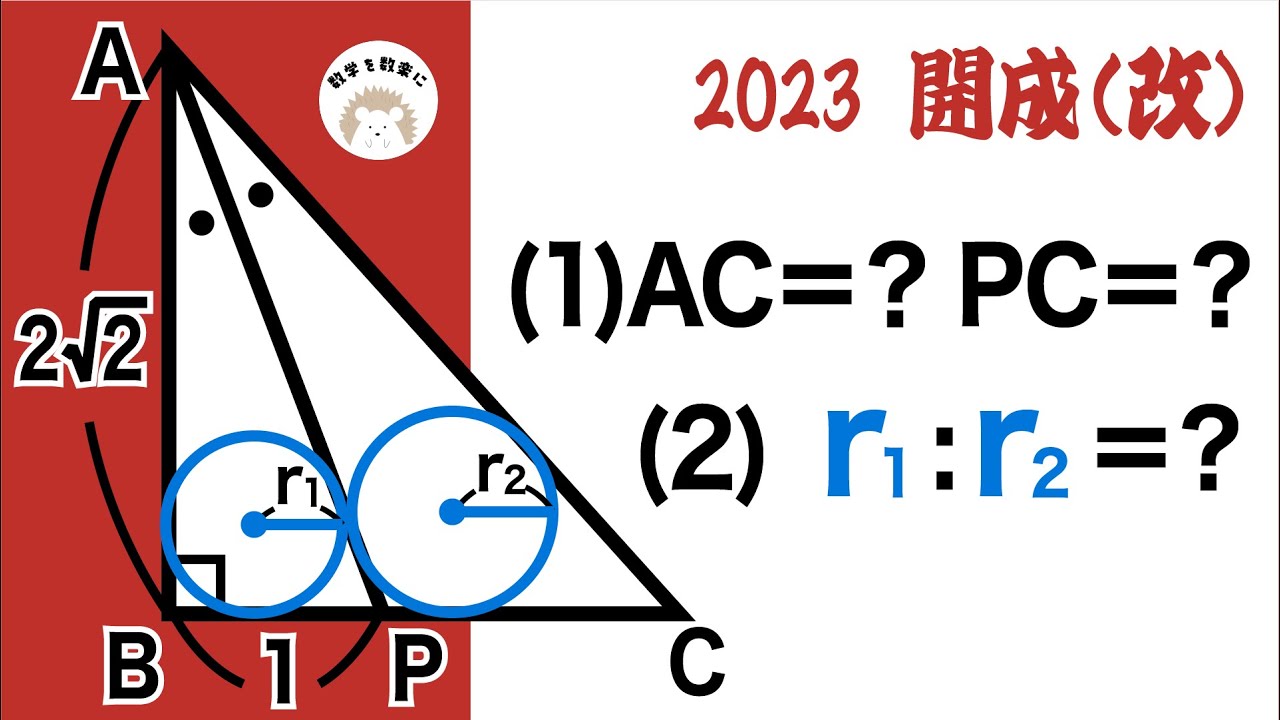
問題文全文(内容文)：
独立な試行の確率についての説明動画です
チャプター：

00:00 はじまり

00:27 独立の言葉の説明

00:45 独立な試行の例

01:46 独立な試行の確率公式

02:18 例題演習(1)

04:51 例題演習(2)

06:41 まとめ

07:27 まとめノート

単元： #数A#確率#数学(高校生)
指導講師： 【楽しい授業動画】あきとんとん
問題文全文(内容文)：
独立な試行の確率についての説明動画です
投稿日：2020.07.19

＜関連動画＞

14兵庫県教員採用試験（数学：1-1番　整数問題）

アイキャッチ画像
単元： #数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#その他#数学(高校生)#教員採用試験
指導講師： ますただ
問題文全文(内容文)：
1⃣-(1)
$2^{2x}-3^{2y} =55$を満たす、$x,y \in \mathbb{ Z }$を求めよ。
この動画を見る　

あなたもダマされる

アイキャッチ画像
単元： #数A#整数の性質#ユークリッド互除法と不定方程式・Ｎ進法#数学(高校生)
指導講師： 数学を数楽に
問題文全文(内容文)：
方程式を解け
$x \times x = 2 \times 2$
この動画を見る　

これなに？

アイキャッチ画像
単元： #数A#図形の性質#空間における垂直と平行と多面体（オイラーの法則）
指導講師： 【楽しい授業動画】あきとんとん
問題文全文(内容文)：
オイラーの多面体定理解説動画です
この動画を見る　

【高校数学】樹形図～改めて図と法則を考える～ 1-5【数学A】

アイキャッチ画像
単元： #数A#場合の数と確率#場合の数#数学(高校生)
指導講師： 【楽しい授業動画】あきとんとん
問題文全文(内容文)：
樹形図　改めて図と法則を考える動画です
この動画を見る　

２つの円と正方形

アイキャッチ画像
単元： #数A#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#数学(高校生)
指導講師： 数学を数楽に
問題文全文(内容文)：
長方形の面積=?
＊図は動画内参照
この動画を見る　
Back to top