2024年慶応義塾普通部算数「公倍数」中学受験指導歴20年以上のプロ解説 - 質問解決D.B.（データベース）
Generic selectors
完全一致検索
タイトルから検索
記事本文から検索
Post Type Selectors
all_unit_post
質問解決D.B.（データベース） > 動画投稿 > 算数(中学受験) > 計算と数の性質 > 約数・倍数を利用する問題 > 2024年慶応義塾普通部算数「公倍数」中学受験指導歴20年以上のプロ解説

2024年慶応義塾普通部算数「公倍数」中学受験指導歴20年以上のプロ解説

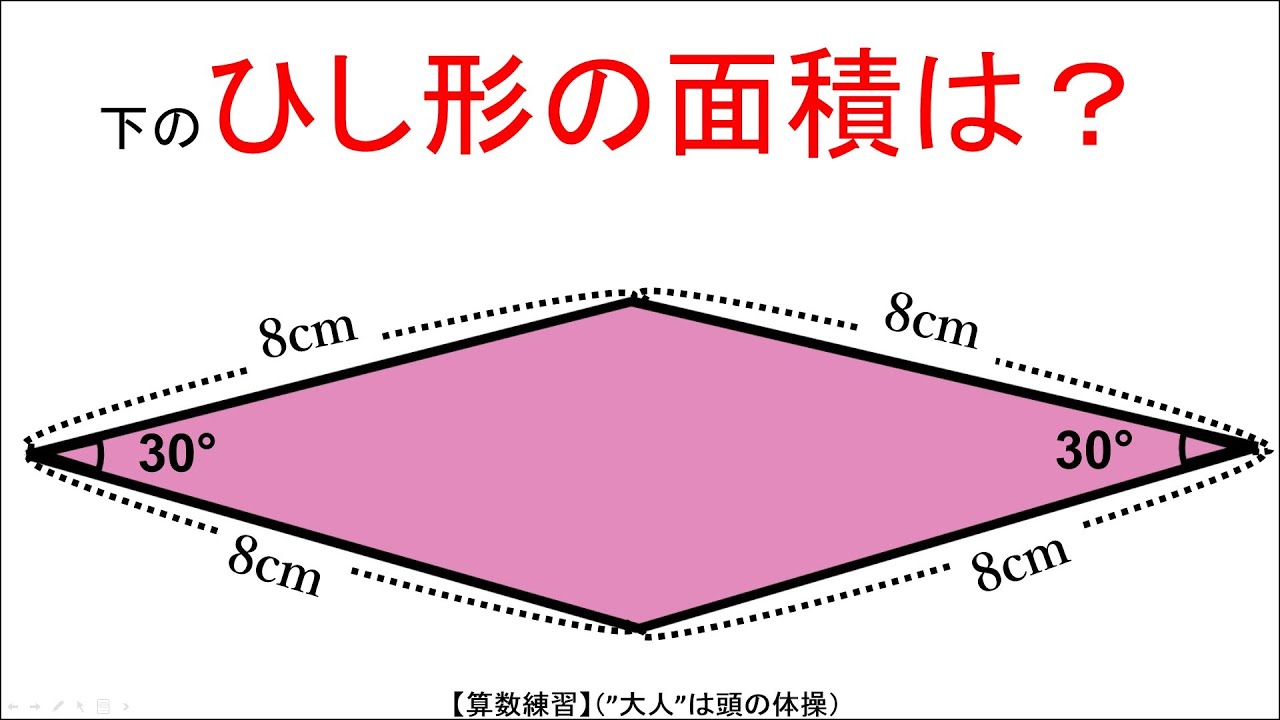
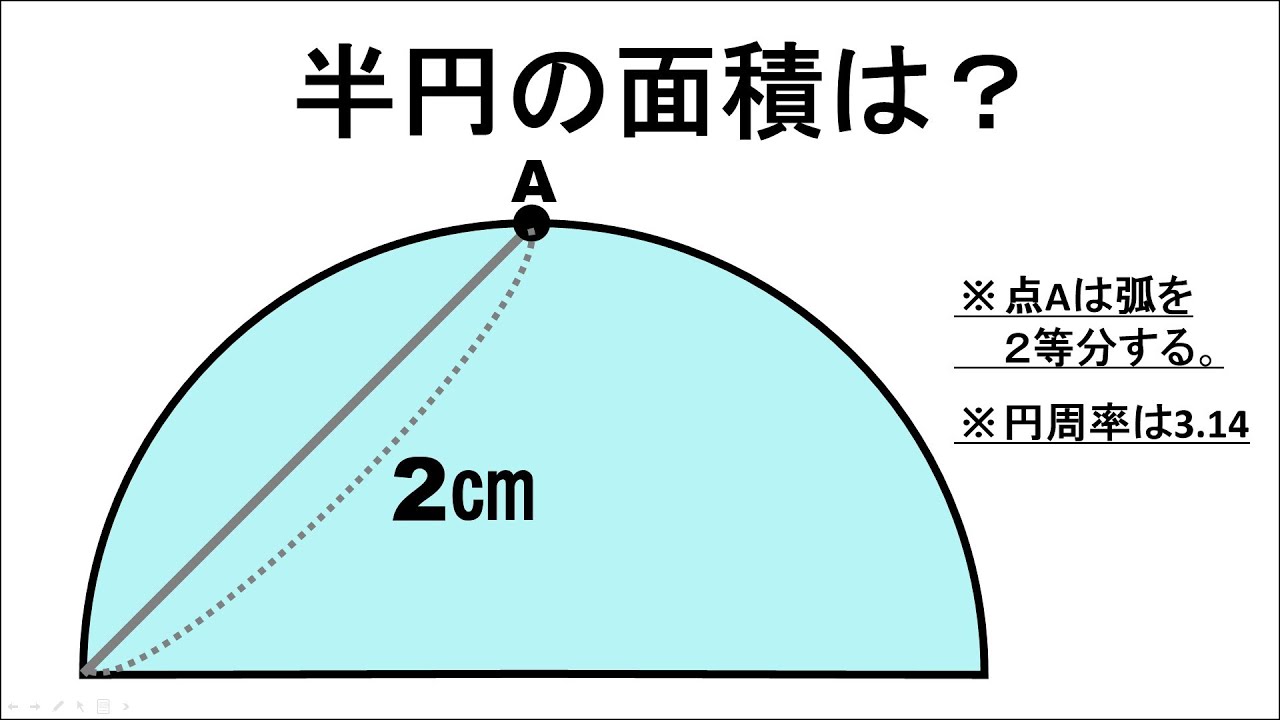
問題文全文(内容文)：
①2から5までの4個の整数のいずれでも割り切れる整数の中で最小の整数は60です.
では,2から9までの8個の整数のいずれでも割り切れる整数の中で,最小の整数はいくつですか.
②2から5までの4個の整数のうちちょうど3個の整数で割り切れる整数の中で,最小の整数は12です.
では,2から9までの8個の整数のうちちょうど6個の整数で割りきれる整数の中で,2番目に小さい整
数はいくつですか.

2024年慶応義塾普通部過去問
単元： #算数(中学受験)#計算と数の性質#約数・倍数を利用する問題
指導講師： 重吉
問題文全文(内容文)：
①2から5までの4個の整数のいずれでも割り切れる整数の中で最小の整数は60です.
では,2から9までの8個の整数のいずれでも割り切れる整数の中で,最小の整数はいくつですか.
②2から5までの4個の整数のうちちょうど3個の整数で割り切れる整数の中で,最小の整数は12です.
では,2から9までの8個の整数のうちちょうど6個の整数で割りきれる整数の中で,2番目に小さい整
数はいくつですか.

2024年慶応義塾普通部過去問
投稿日：2024.07.16

＜関連動画＞

正2.5角形があるとすればどんな形？

アイキャッチ画像
単元： #算数(中学受験)#平面図形#平面図形その他
指導講師： 【楽しい授業動画】あきとんとん
問題文全文(内容文)：
正2.5角形が星形になるという説明
この動画を見る　

GW勉強予定ありますか？

アイキャッチ画像
単元： #算数(中学受験)#その他#その他
指導講師： 【楽しい授業動画】あきとんとん
問題文全文(内容文)：
おすすめの勉強法説明動画です
この動画を見る　

【受験算数】平面図形：豊島岡過去問～正方形をはみ出る円の面積の求め方

アイキャッチ画像
単元： #算数(中学受験)#過去問解説(学校別)#平面図形#平面図形その他
指導講師： 理数個別チャンネル
問題文全文(内容文)：
豊島岡女子学園の過去問の解説します。
正方形をはみ出る円の面積の求め方に関して解説していきます.
この動画を見る　

【受験算数】回転体：三角形の回転体【予習シリーズ算数・小5下】

アイキャッチ画像
単元： #算数(中学受験)#立体図形#体積・表面積・回転体・水量・変化のグラフ
教材： #予習シ#予習シ算数・小5下#中学受験教材
指導講師： 理数個別チャンネル
問題文全文(内容文)：
図のような図形を軸ℓを中心に回転させた時にできる立体の体積を求めなさい。ただしABの真ん中にEが来るものとする。【予習シリーズ】【空間図形】
この動画を見る　

中3生も解けるし　どっちが大きい？

アイキャッチ画像
単元： #数Ⅰ#数A#図形の性質#図形と計量#立体図形#立体図形その他#数学(高校生)
指導講師： 数学を数楽に
問題文全文(内容文)：
xとyどっちが大きい？
＊図は動画内参照
この動画を見る　
PAGE TOP