 重吉
重吉
 重吉
重吉
※下の画像部分をクリックすると、先生の紹介ページにリンクします。
2024年明治大付属明治中算数「食塩水濃度」中学受験指導歴20年以上のプロ解説

単元:
#算数(中学受験)#過去問解説(学校別)#文章題#売買損益と食塩水#明治大学附属明治中学
指導講師:
重吉
問題文全文(内容文):
容器Aには6%の食塩水が300g、容器Bには12%の食塩水が500g入っています。
両方の容器から同じ量の食塩水を同時に取り出し、それぞれもう一方の容器に入れたところ、Aに入っている食塩水の濃さは10%になりました。
Bに入っている食塩水の濃さは□%になります。
出典:2024年明治大学付属明治中学校 入試問題
この動画を見る
容器Aには6%の食塩水が300g、容器Bには12%の食塩水が500g入っています。
両方の容器から同じ量の食塩水を同時に取り出し、それぞれもう一方の容器に入れたところ、Aに入っている食塩水の濃さは10%になりました。
Bに入っている食塩水の濃さは□%になります。
出典:2024年明治大学付属明治中学校 入試問題
2024年明治大付属明治中算数「食塩水濃度」中学受験指導歴20年以上のプロ解説

単元:
#算数(中学受験)#文章題#売買損益と食塩水
指導講師:
重吉
問題文全文(内容文):
容器$A$には6%の食塩水が300g,容器$B$には12%の食塩水が500g入っています.
両方の容器から同じ量の食塩水を同時に取り出し,それぞれもう一方の容器に入れたところ,
$A$に入っている食塩水の濃さは10%になりました.
$B$に入っている食塩水の濃さは$\Box$になります.
$\Box$を求めよ.
2024年明治大付属明治中過去問
この動画を見る
容器$A$には6%の食塩水が300g,容器$B$には12%の食塩水が500g入っています.
両方の容器から同じ量の食塩水を同時に取り出し,それぞれもう一方の容器に入れたところ,
$A$に入っている食塩水の濃さは10%になりました.
$B$に入っている食塩水の濃さは$\Box$になります.
$\Box$を求めよ.
2024年明治大付属明治中過去問
2024年慶応義塾普通部算数「公倍数」中学受験指導歴20年以上のプロ解説

単元:
#算数(中学受験)#計算と数の性質#約数・倍数を利用する問題#過去問解説(学校別)#慶應義塾普通部
指導講師:
重吉
問題文全文(内容文):
①
2から5までの4個の整数のいずれでもわり切れる整数の中で、最小の整数は60です。
では、2から9までの8個の整数のいずれでもわり切れる整数の中で、最小の整数はいくつですか。
②
2から5までの4個のせいすうのうちちょうど3個の整数でわり切れる整数の中で、最小の整数は12です。
では、2から9までの8個の整数のうちちょうど6個の整数でわり切れる整数の中で、2番目に小さい整数はいくつですか。
出典:2024年慶應義塾普通部 入試問題
この動画を見る
①
2から5までの4個の整数のいずれでもわり切れる整数の中で、最小の整数は60です。
では、2から9までの8個の整数のいずれでもわり切れる整数の中で、最小の整数はいくつですか。
②
2から5までの4個のせいすうのうちちょうど3個の整数でわり切れる整数の中で、最小の整数は12です。
では、2から9までの8個の整数のうちちょうど6個の整数でわり切れる整数の中で、2番目に小さい整数はいくつですか。
出典:2024年慶應義塾普通部 入試問題
2024年慶応義塾普通部算数「公倍数」中学受験指導歴20年以上のプロ解説

単元:
#算数(中学受験)#計算と数の性質#約数・倍数を利用する問題
指導講師:
重吉
問題文全文(内容文):
①2から5までの4個の整数のいずれでも割り切れる整数の中で最小の整数は60です.
では,2から9までの8個の整数のいずれでも割り切れる整数の中で,最小の整数はいくつですか.
②2から5までの4個の整数のうちちょうど3個の整数で割り切れる整数の中で,最小の整数は12です.
では,2から9までの8個の整数のうちちょうど6個の整数で割りきれる整数の中で,2番目に小さい整
数はいくつですか.
2024年慶応義塾普通部過去問
この動画を見る
①2から5までの4個の整数のいずれでも割り切れる整数の中で最小の整数は60です.
では,2から9までの8個の整数のいずれでも割り切れる整数の中で,最小の整数はいくつですか.
②2から5までの4個の整数のうちちょうど3個の整数で割り切れる整数の中で,最小の整数は12です.
では,2から9までの8個の整数のうちちょうど6個の整数で割りきれる整数の中で,2番目に小さい整
数はいくつですか.
2024年慶応義塾普通部過去問
2024年昭和学院秀英中算数「相似」中学受験指導歴20年以上のプロ解説

単元:
#算数(中学受験)#過去問解説(学校別)#平面図形#相似と相似を利用した問題#昭和学院秀英中学
指導講師:
重吉
問題文全文(内容文):
正方形の紙を下の図のように折ったときBG=3cm,BE=4cm,EG=5cmとなりました。
このとき、三角形IHFの面積は[イ]㎠です。
出典:2024年昭和学院秀英中学校 入試問題
この動画を見る
正方形の紙を下の図のように折ったときBG=3cm,BE=4cm,EG=5cmとなりました。
このとき、三角形IHFの面積は[イ]㎠です。
出典:2024年昭和学院秀英中学校 入試問題
2024年昭和学院秀英中算数「相似」中学受験指導歴20年以上のプロ解説

2024年立教新座中算数「和差算」中学受験指導歴20年のプロ解説

単元:
#算数(中学受験)#文章題#和差算・植木算・分配算・倍数算・年齢算・相当算・つるかめ算
指導講師:
重吉
問題文全文(内容文):
$4$つの異なる整数,$A,B,C,D$があります.
これらの整数のうち異なる2つをたすと全部で6つの数ができますが,この6つの数の中に同じ数が
あったので,できた数は$10,13,15,17,20$の5種類でした.4つの整数$A,B,C,D$の積をもとめなさい.
2024年立教新座中過去問
この動画を見る
$4$つの異なる整数,$A,B,C,D$があります.
これらの整数のうち異なる2つをたすと全部で6つの数ができますが,この6つの数の中に同じ数が
あったので,できた数は$10,13,15,17,20$の5種類でした.4つの整数$A,B,C,D$の積をもとめなさい.
2024年立教新座中過去問
2024年栄東中A日程算数「グラフの利用(速さ)」中学受験指導20年のプロ解説
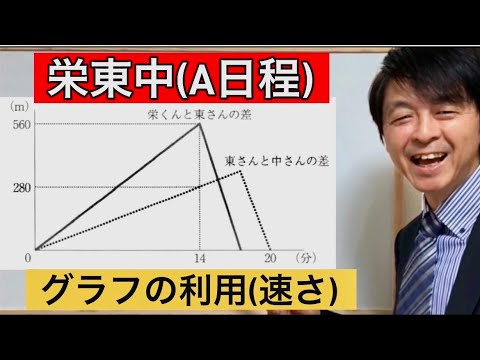
単元:
#算数(中学受験)#過去問解説(学校別)#速さ#ダイヤグラム#栄東中学
指導講師:
重吉
問題文全文(内容文):
それぞれ下線、〇を求めよ
(1)
動画内のグラフより、栄は____分で、中は____分でゴールする。
よって時間の比 栄:中=____:____=____:____
速さの比 栄:中=____:____
(2)
栄と中の速さの比____:____は、同じ時間(14分)で走った距離の比と等しい。
よって動画内の図より栄がゴールした時の二人の差は〇-〇=〇=____+____=____m
よって、①=____m$\div$=____mなので、マラソンコース〇=____$\times$____=____m
(3)
栄がゴールした14分時点で、東はゴール手前560m地点にいるので、14分で____-____=____m走った。
よって、東の分速は____$\div$____=____m/分なので2800mのマラソンコースを走るのに
____$\div$____=____分=____分____秒かかる。
この動画を見る
それぞれ下線、〇を求めよ
(1)
動画内のグラフより、栄は____分で、中は____分でゴールする。
よって時間の比 栄:中=____:____=____:____
速さの比 栄:中=____:____
(2)
栄と中の速さの比____:____は、同じ時間(14分)で走った距離の比と等しい。
よって動画内の図より栄がゴールした時の二人の差は〇-〇=〇=____+____=____m
よって、①=____m$\div$=____mなので、マラソンコース〇=____$\times$____=____m
(3)
栄がゴールした14分時点で、東はゴール手前560m地点にいるので、14分で____-____=____m走った。
よって、東の分速は____$\div$____=____m/分なので2800mのマラソンコースを走るのに
____$\div$____=____分=____分____秒かかる。
2024年栄東中A日程算数「グラフの利用(速さ)」中学受験指導20年のプロ解説

2024年東邦大付属東邦中算数「相似」中学受験指導歴20年のプロ解説

単元:
#算数(中学受験)#過去問解説(学校別)#平面図形#相似と相似を利用した問題#東邦大学付属東邦中学
指導講師:
重吉
問題文全文(内容文):
動画内の図のような、三角形$ABC$があります。
このとき、$AD$の長さは何cmか求めなさい。
ただし、同じしるしはそれぞれ同じ角度を表しています。
出典:東邦大学付属東邦中学校 入試問題
この動画を見る
動画内の図のような、三角形$ABC$があります。
このとき、$AD$の長さは何cmか求めなさい。
ただし、同じしるしはそれぞれ同じ角度を表しています。
出典:東邦大学付属東邦中学校 入試問題
2024年東邦大付属東邦中算数「相似」中学受験指導歴20年のプロ解説

2024年洗足学園中算数「相当算」中学受験指導歴20年のプロ解説

単元:
#算数(中学受験)#過去問解説(学校別)#文章題#和差算・植木算・分配算・倍数算・年齢算・相当算・つるかめ算#洗足学園中学
指導講師:
重吉
問題文全文(内容文):
Aさんが買い物をしました。
最初の店では所持金の$\displaystyle \frac{1}{2}$より200円多く使い、2番目の店では残った所持金の$\displaystyle \frac{1}{3}$よりも400円多く使いました。
3番目の店で残った所持金の$\displaystyle \frac{1}{4}$よりも600円多く使ったところ、所持金をすべて使い切りました。
Aさんは、はじめに何円持っていましたか。
出典:2024年洗足学園中学高等学校 入試問題
この動画を見る
Aさんが買い物をしました。
最初の店では所持金の$\displaystyle \frac{1}{2}$より200円多く使い、2番目の店では残った所持金の$\displaystyle \frac{1}{3}$よりも400円多く使いました。
3番目の店で残った所持金の$\displaystyle \frac{1}{4}$よりも600円多く使ったところ、所持金をすべて使い切りました。
Aさんは、はじめに何円持っていましたか。
出典:2024年洗足学園中学高等学校 入試問題
2024年洗足学園中算数「相当算」中学受験指導歴20年のプロ解説

単元:
#算数(中学受験)#文章題#和差算・植木算・分配算・倍数算・年齢算・相当算・つるかめ算
指導講師:
重吉
問題文全文(内容文):
(1)はじめの所持金を求めよ.
(2)2番目の店に行った時の所持金を求めよ.
(3)3番目のみ背に行った時の所持金を求めよ.
2024年洗足学園中過去問
この動画を見る
(1)はじめの所持金を求めよ.
(2)2番目の店に行った時の所持金を求めよ.
(3)3番目のみ背に行った時の所持金を求めよ.
2024年洗足学園中過去問
2024年四天王寺中算数「ニュートン算」中学受験指導歴20年のプロ解説

単元:
#算数(中学受験)#過去問解説(学校別)#文章題#仕事算とニュートン算#四天王寺中学
指導講師:
重吉
問題文全文(内容文):
ある牧場には、はじめ牧草が生えていて、その後も1日に一定の量の牧草が生えます。
この牧場に牛を5頭放すと120日間で牧草を食べつくし、牛を10頭放すと30日間で牧草を食べつくします。
①1日に生える牧草の量は、牛1頭が1日に食べる牧草の量の何倍ですか。
②この牧場に牛を20頭放すと何日間で牧草を食べつくしますか。
出典:2024年四天王寺中学校 入試問題
この動画を見る
ある牧場には、はじめ牧草が生えていて、その後も1日に一定の量の牧草が生えます。
この牧場に牛を5頭放すと120日間で牧草を食べつくし、牛を10頭放すと30日間で牧草を食べつくします。
①1日に生える牧草の量は、牛1頭が1日に食べる牧草の量の何倍ですか。
②この牧場に牛を20頭放すと何日間で牧草を食べつくしますか。
出典:2024年四天王寺中学校 入試問題
2024年四天王寺中算数「ニュートン算」中学受験指導歴20年のプロ解説

単元:
#算数(中学受験)#文章題#仕事算とニュートン算
指導講師:
重吉
問題文全文(内容文):
ある牧場には,はじめ牧草が生えていて,その後も1日に一定の量の牧草が生えます.
この牧場に牛を5頭放すと120日間で牧草を食べ尽くし,牛を10頭放すと30日間で牧草を食べ尽くします.
①1日に生える牧草の量は,牛1頭が1日に食べる牧草の量の何倍ですか.
②この牧場に牛を20頭放すと何日間で牧草を食べ尽くしますか.
2024年四天王寺中過去問
この動画を見る
ある牧場には,はじめ牧草が生えていて,その後も1日に一定の量の牧草が生えます.
この牧場に牛を5頭放すと120日間で牧草を食べ尽くし,牛を10頭放すと30日間で牧草を食べ尽くします.
①1日に生える牧草の量は,牛1頭が1日に食べる牧草の量の何倍ですか.
②この牧場に牛を20頭放すと何日間で牧草を食べ尽くしますか.
2024年四天王寺中過去問
小6基礎トレ6月18日⑧「線分の比」

小6基礎トレ6月18日⑧「線分の比」

2024年洛南高校附属中算数「旅人算」中学受験指導歴20年のプロ解説

単元:
#算数(中学受験)#過去問解説(学校別)#速さ#旅人算・通過算・流水算#洛南高校附属中学
指導講師:
重吉
問題文全文(内容文):
地点Aと地点Bの間を、太郎さんと花子さんが休むことなく一定の速さで繰り返し往復します。
太郎さんはAを、花子さんはBを同時に出発します。
2人が1往復する間に、2人は2回すれ違い、1回目、2回目にすれ違ったのはAからそれぞれ800m、400m地点でした。
このとき、次の問に答えなさい。
(1)
AB間の距離は何mですか。
(2)
2人が初めて同時に地点Aに着くとき、太郎さんは出発してから何m進みましたか。
出典:2024年洛南高等学校附属中学校 入試問題
この動画を見る
地点Aと地点Bの間を、太郎さんと花子さんが休むことなく一定の速さで繰り返し往復します。
太郎さんはAを、花子さんはBを同時に出発します。
2人が1往復する間に、2人は2回すれ違い、1回目、2回目にすれ違ったのはAからそれぞれ800m、400m地点でした。
このとき、次の問に答えなさい。
(1)
AB間の距離は何mですか。
(2)
2人が初めて同時に地点Aに着くとき、太郎さんは出発してから何m進みましたか。
出典:2024年洛南高等学校附属中学校 入試問題
2024年洛南高校附属中算数「旅人算」中学受験指導歴20年のプロ解説

単元:
#算数(中学受験)#速さ#旅人算・通過算・流水算
指導講師:
重吉
問題文全文(内容文):
地点$A$と地点$B$の間を,太郎さんと花子さんが休むことなく一定の速さで繰り返し往復します.
太郎さんは$A$を,花子さんは$B$を同時に出発します.
2人が1往復する間に,2人は2回すれ違い,1回目,2回目にすれ違ったのは$A$からそれぞれ$800m$,$400m$の地点でした.
このとき,次の問いに答えなさい.
(1)$AB$間の距離は何mですか.
(2)2人が初めて同時に地点$A$に着くとき,太郎さんは出発してから何m進みましたか.
2024年洛南高校附属中過去問
この動画を見る
地点$A$と地点$B$の間を,太郎さんと花子さんが休むことなく一定の速さで繰り返し往復します.
太郎さんは$A$を,花子さんは$B$を同時に出発します.
2人が1往復する間に,2人は2回すれ違い,1回目,2回目にすれ違ったのは$A$からそれぞれ$800m$,$400m$の地点でした.
このとき,次の問いに答えなさい.
(1)$AB$間の距離は何mですか.
(2)2人が初めて同時に地点$A$に着くとき,太郎さんは出発してから何m進みましたか.
2024年洛南高校附属中過去問
2024年慶応義塾中等部算数「相似と面積」中学受験指導歴20年のプロ解説

単元:
#算数(中学受験)#平面図形#相似と相似を利用した問題
指導講師:
重吉
問題文全文(内容文):
(い)+(う)$=26cm^2$の時,平行四辺形の面積は?
2024年慶応義塾中過去問
この動画を見る
(い)+(う)$=26cm^2$の時,平行四辺形の面積は?
2024年慶応義塾中過去問
2024年慶応義塾中等部算数「相似と面積」中学受験指導歴20年のプロ解説

単元:
#算数(中学受験)#過去問解説(学校別)#平面図形#相似と相似を利用した問題#慶應義塾中等部
指導講師:
重吉
問題文全文(内容文):
動画内の図のように、平行四辺形に対角線をひき、さらに底辺を三等分する点のうち1つと平行四辺形の頂点を結んで、平行四辺形を4つの部分㋐~㋓に分けました。
㋑の部分と㋒の部分の面積の和が26㎠であるとき、この平行四辺形の面積は$㋐\displaystyle \frac{㋑}{㋒}$㎠です。
出典:2024年慶應義塾中等部 入試問題
この動画を見る
動画内の図のように、平行四辺形に対角線をひき、さらに底辺を三等分する点のうち1つと平行四辺形の頂点を結んで、平行四辺形を4つの部分㋐~㋓に分けました。
㋑の部分と㋒の部分の面積の和が26㎠であるとき、この平行四辺形の面積は$㋐\displaystyle \frac{㋑}{㋒}$㎠です。
出典:2024年慶應義塾中等部 入試問題
2024年渋谷教育学園渋谷中算数「正多角形の角度」中学受験指導歴20年のプロ解説

単元:
#算数(中学受験)#平面図形#図形の移動#平面図形その他
指導講師:
重吉
問題文全文(内容文):
下の図は,円と正六角形と正十角形かたできています.
点$O$は,円の中心です.このとき,(あ)の角の大きさは何度ですか.
2024年渋谷教育学園渋谷中過去問
この動画を見る
下の図は,円と正六角形と正十角形かたできています.
点$O$は,円の中心です.このとき,(あ)の角の大きさは何度ですか.
2024年渋谷教育学園渋谷中過去問
2024年渋谷教育学園渋谷中算数「正多角形の角度」中学受験指導歴20年のプロ解説

単元:
#算数(中学受験)#過去問解説(学校別)#平面図形#角度と面積#渋谷教育学園渋谷中学
指導講師:
重吉
問題文全文(内容文):
動画内の図は、円と正六角形と正十角形からできています。
点Oは、円の中心です。
このとき、㋐の角の大きさは何度ですか。
出典:2024年渋谷教育学園渋谷中学高等学校 入試問題
この動画を見る
動画内の図は、円と正六角形と正十角形からできています。
点Oは、円の中心です。
このとき、㋐の角の大きさは何度ですか。
出典:2024年渋谷教育学園渋谷中学高等学校 入試問題
雙葉中2024年算数入試問題「流水算」個別指導塾講師歴20年のプロ解説

雙葉中2024年算数入試問題「流水算」個別指導塾講師歴20年のプロ解説

単元:
#算数(中学受験)#過去問解説(学校別)#速さ#旅人算・通過算・流水算#雙葉中学
指導講師:
重吉
問題文全文(内容文):
下流にあるA地点と上流にあるB地点は、5733m離れています。
兄はボートをこいでA地点を出発し、B地点に着いたら折り返し、2時間後にA地点に戻ってきました。
静水時の兄がこぐボートの速さと川の流れの速さは一定で、その日は10:3です。(式と計算と答え)
(1)
兄はA地点を出発してから、何時間何分後にB地点に着きましたか。
(2)
川の流れの速さは分速何mですか。
(3)
兄がA地点を出発したのと同時に、弟もボートでB地点を出発しました。
弟は、ボートをこがずに川の流れまかせて進み、兄と2回出会ってA地点に着きました。
弟が2回目に兄と出会うのは、2人が出発してから何時間何分何秒後でしたか。
出典:2024年雙葉中学校 入試問題
この動画を見る
下流にあるA地点と上流にあるB地点は、5733m離れています。
兄はボートをこいでA地点を出発し、B地点に着いたら折り返し、2時間後にA地点に戻ってきました。
静水時の兄がこぐボートの速さと川の流れの速さは一定で、その日は10:3です。(式と計算と答え)
(1)
兄はA地点を出発してから、何時間何分後にB地点に着きましたか。
(2)
川の流れの速さは分速何mですか。
(3)
兄がA地点を出発したのと同時に、弟もボートでB地点を出発しました。
弟は、ボートをこがずに川の流れまかせて進み、兄と2回出会ってA地点に着きました。
弟が2回目に兄と出会うのは、2人が出発してから何時間何分何秒後でしたか。
出典:2024年雙葉中学校 入試問題
聖光学院中2024年算数入試問題「倍数の和」個別指導塾講師歴20年のプロ解説

単元:
#算数(中学受験)#計算と数の性質#約数・倍数を利用する問題#過去問解説(学校別)#聖光学院中学
指導講師:
重吉
問題文全文(内容文):
【聖光学院中2024年算数入試問題】
1から120までの整数のうち、3でも5でも割り切れない数の総和を求めなさい。
この動画を見る
【聖光学院中2024年算数入試問題】
1から120までの整数のうち、3でも5でも割り切れない数の総和を求めなさい。
豊島岡女子学園中2024年算数入試問題「面積の和(3)」個別指導塾講師歴20年のプロ解説

単元:
#算数(中学受験)#過去問解説(学校別)#平面図形#角度と面積#豊島岡女子学園中学
指導講師:
重吉
問題文全文(内容文):
動画内の図のような直角三角形PQRと正方形STUVがあります。
辺QRの長さと正方形の1辺の長さが等しく、辺PRの長さと正方形の1辺の長さの和が4cmであるとき、2つの図形の面積の和は何cmですか。
この動画を見る
動画内の図のような直角三角形PQRと正方形STUVがあります。
辺QRの長さと正方形の1辺の長さが等しく、辺PRの長さと正方形の1辺の長さの和が4cmであるとき、2つの図形の面積の和は何cmですか。
2024年豊島岡女子学園中算数「面積の和(2)」個別指導塾講師歴20年のプロ解説
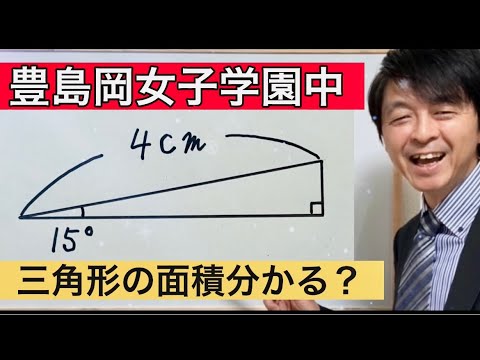
単元:
#算数(中学受験)#過去問解説(学校別)#平面図形#角度と面積#豊島岡女子学園中学
指導講師:
重吉
問題文全文(内容文):
動画内の図のような三角形GHI,JKL,MNOがあります。
辺GIの長さと辺JKの長さ、辺の長さと辺NOの長さがそれぞれ等しく、辺GHの長さと辺MNの長さの和が4cmであるとき、3つの三角形の面積の和は何cm²ですか。
この動画を見る
動画内の図のような三角形GHI,JKL,MNOがあります。
辺GIの長さと辺JKの長さ、辺の長さと辺NOの長さがそれぞれ等しく、辺GHの長さと辺MNの長さの和が4cmであるとき、3つの三角形の面積の和は何cm²ですか。
豊島岡女子学園中2024年算数入試問題「面積の和(1)」個別指導塾講師歴20年のプロ解説

単元:
#算数(中学受験)#過去問解説(学校別)#平面図形#角度と面積#豊島岡女子学園中学
指導講師:
重吉
問題文全文(内容文):
動画内の図のような三角形ABC,DEFがあります。
辺ACの長さと辺DEの長さが等しく、辺ABと辺DFの長さの和が4cmであるとき、2つの三角形の面積の和は何cm²ですか。
この動画を見る
動画内の図のような三角形ABC,DEFがあります。
辺ACの長さと辺DEの長さが等しく、辺ABと辺DFの長さの和が4cmであるとき、2つの三角形の面積の和は何cm²ですか。
2019武蔵中学校算数①

単元:
#算数(中学受験)#計算と数の性質#約数・倍数を利用する問題#過去問解説(学校別)#武蔵中学
指導講師:
重吉
問題文全文(内容文):
【2019武蔵中学校】
次の各問に答えなさい。
(1)次の㋐から㋓にあてはまる数を書き入れなさい。
31は小さい方から数えて[㋐]番目の素数であり、1以上31以下のすべての素数の和は[㋑]です。
㋑の約数は全部で[㋒]個あり、その㋒個の約数すべての逆数の和は[㋓]です。
ただし、素数とは1とその数以外に約教をもたない数です。
また、1は要数ではありません。
(この下に計算などを書いてもかまいません)
この動画を見る
【2019武蔵中学校】
次の各問に答えなさい。
(1)次の㋐から㋓にあてはまる数を書き入れなさい。
31は小さい方から数えて[㋐]番目の素数であり、1以上31以下のすべての素数の和は[㋑]です。
㋑の約数は全部で[㋒]個あり、その㋒個の約数すべての逆数の和は[㋓]です。
ただし、素数とは1とその数以外に約教をもたない数です。
また、1は要数ではありません。
(この下に計算などを書いてもかまいません)




