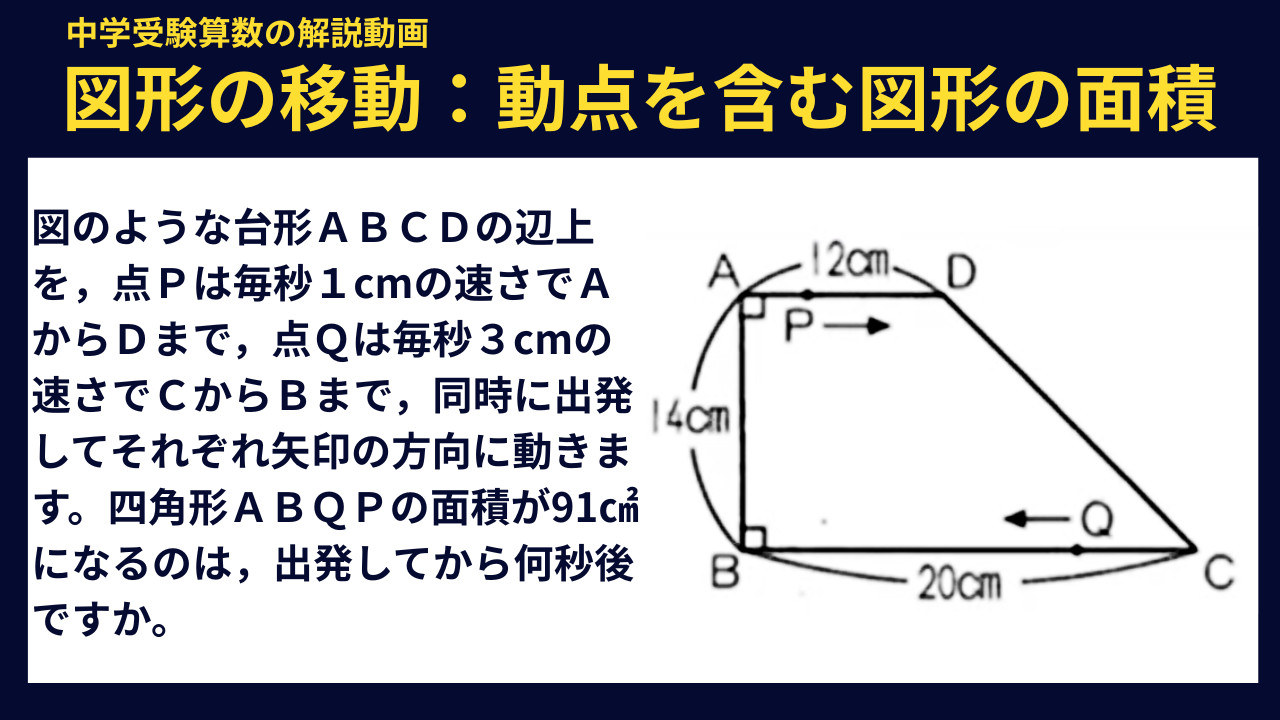
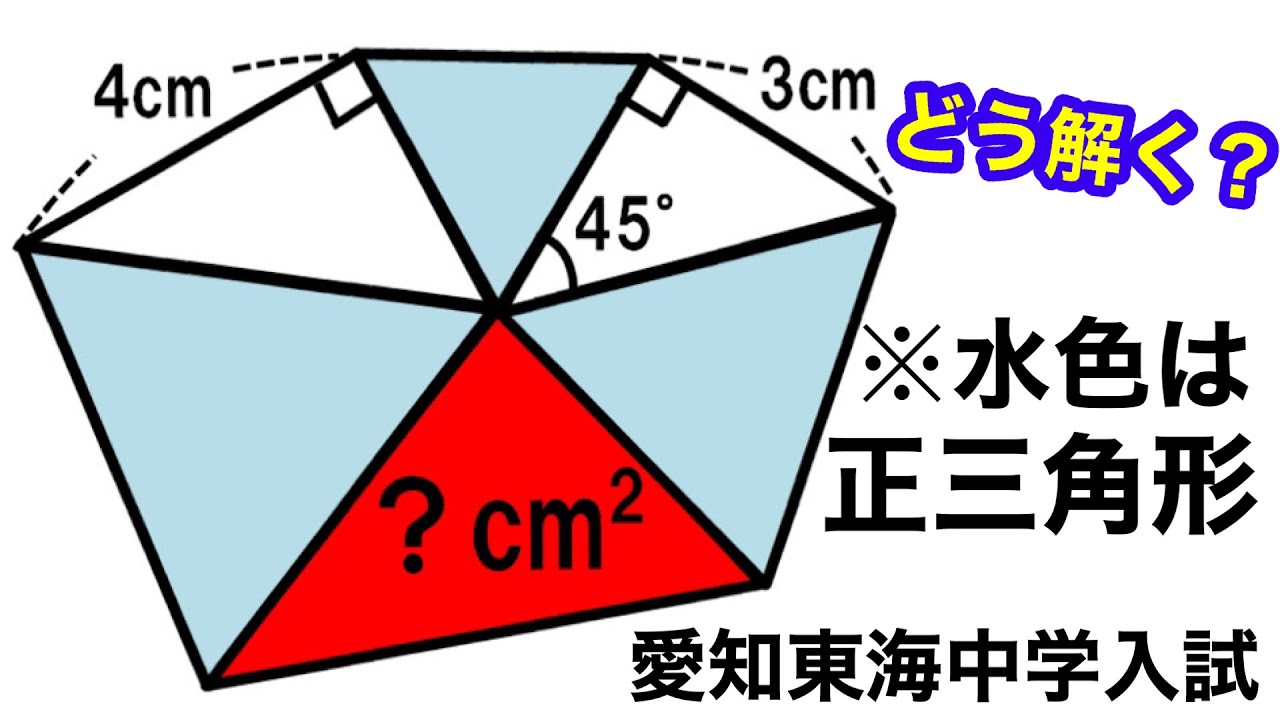
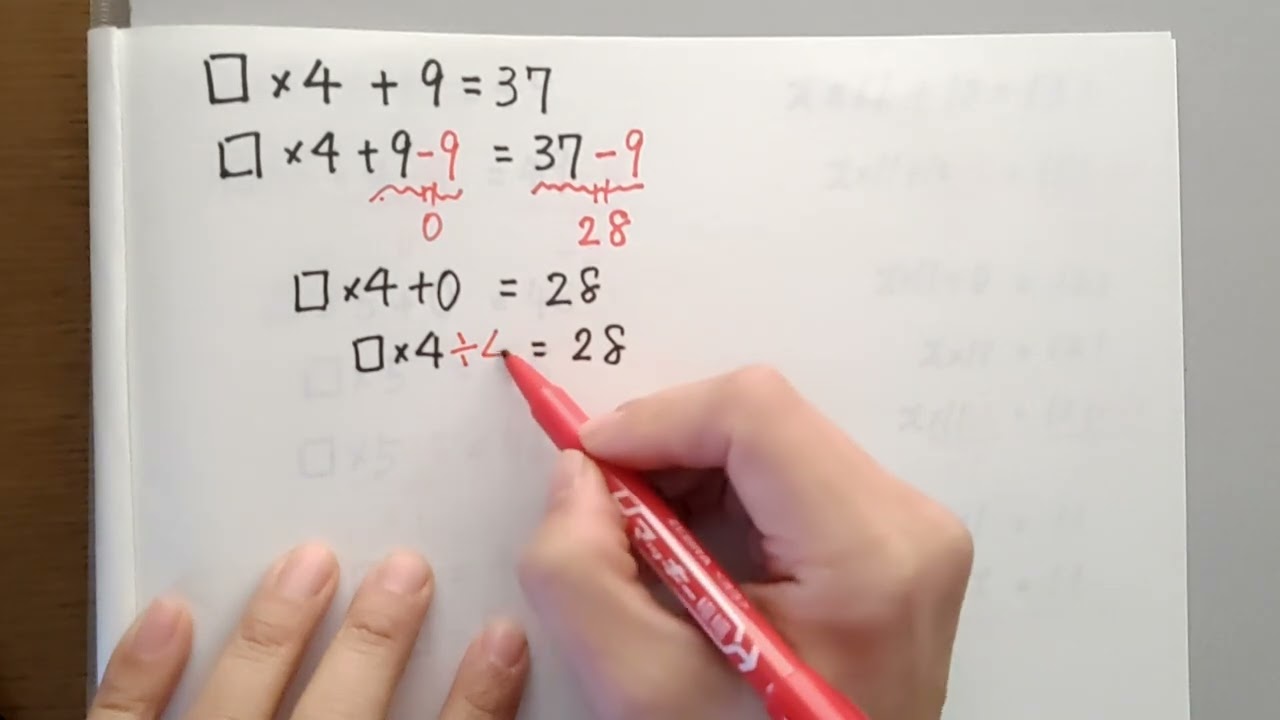問題文全文(内容文)：
下流にあるA地点と上流にあるB地点は、5733m離れています。
兄はボートをこいでA地点を出発し、B地点に着いたら折り返し、2時間後にA地点に戻ってきました。
静水時の兄がこぐボートの速さと川の流れの速さは一定で、その日は10:3です。（式と計算と答え）

（1）
兄はA地点を出発してから、何時間何分後にB地点に着きましたか。

（2）
川の流れの速さは分速何mですか。

（3）
兄がA地点を出発したのと同時に、弟もボートでB地点を出発しました。
弟は、ボートをこがずに川の流れまかせて進み、兄と2回出会ってA地点に着きました。
弟が2回目に兄と出会うのは、2人が出発してから何時間何分何秒後でしたか。

出典：2024年雙葉中学校　入試問題