問題文全文(内容文):
高校受験対策・関数37
Q.
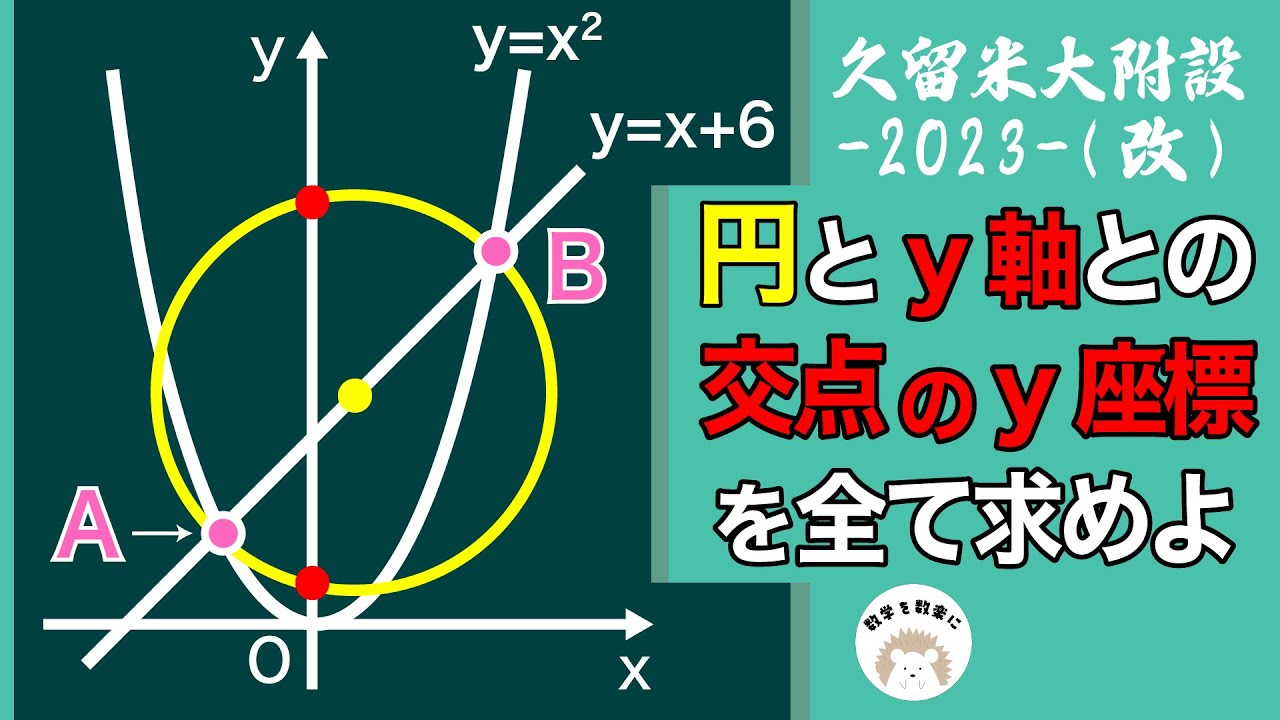
右の図において、直線①は関数$y=x+6$のグラフであり、曲線②は関数$y=ax^2$のグラフである。 2点、A・Bはともに直線①と曲線②との交点で、点Aの$x$座標は$-3$、 点Bの$x$座標は$6$であり、点Cは直線①と$y$軸との交点である。
また、原点を$o$とするとき、点Dは$y$軸上の点で$CO:OD=6:7$であり、 その$y$座標は負である。
点Eは線分AD上の点でAE=EDである。 さらに点Fは$x$軸上の点で、線分BFは$y$軸に平行である。 このとき次の問いに答えなさい。
①曲線②の式$y=ax^2$の$a$の値を求めなさい。
➁直線EFの式を求めなさい。
③線分AFと線分BOとの交点をGとするとき、三角形AGBと三角形DFGの曲積の比を最も簡単な整数の比で表しなさい。
高校受験対策・関数37
Q.
右の図において、直線①は関数$y=x+6$のグラフであり、曲線②は関数$y=ax^2$のグラフである。 2点、A・Bはともに直線①と曲線②との交点で、点Aの$x$座標は$-3$、 点Bの$x$座標は$6$であり、点Cは直線①と$y$軸との交点である。
また、原点を$o$とするとき、点Dは$y$軸上の点で$CO:OD=6:7$であり、 その$y$座標は負である。
点Eは線分AD上の点でAE=EDである。 さらに点Fは$x$軸上の点で、線分BFは$y$軸に平行である。 このとき次の問いに答えなさい。
①曲線②の式$y=ax^2$の$a$の値を求めなさい。
➁直線EFの式を求めなさい。
③線分AFと線分BOとの交点をGとするとき、三角形AGBと三角形DFGの曲積の比を最も簡単な整数の比で表しなさい。
単元:
#数学(中学生)#中3数学#2次関数
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
高校受験対策・関数37
Q.
右の図において、直線①は関数$y=x+6$のグラフであり、曲線②は関数$y=ax^2$のグラフである。 2点、A・Bはともに直線①と曲線②との交点で、点Aの$x$座標は$-3$、 点Bの$x$座標は$6$であり、点Cは直線①と$y$軸との交点である。
また、原点を$o$とするとき、点Dは$y$軸上の点で$CO:OD=6:7$であり、 その$y$座標は負である。
点Eは線分AD上の点でAE=EDである。 さらに点Fは$x$軸上の点で、線分BFは$y$軸に平行である。 このとき次の問いに答えなさい。
①曲線②の式$y=ax^2$の$a$の値を求めなさい。
➁直線EFの式を求めなさい。
③線分AFと線分BOとの交点をGとするとき、三角形AGBと三角形DFGの曲積の比を最も簡単な整数の比で表しなさい。
高校受験対策・関数37
Q.
右の図において、直線①は関数$y=x+6$のグラフであり、曲線②は関数$y=ax^2$のグラフである。 2点、A・Bはともに直線①と曲線②との交点で、点Aの$x$座標は$-3$、 点Bの$x$座標は$6$であり、点Cは直線①と$y$軸との交点である。
また、原点を$o$とするとき、点Dは$y$軸上の点で$CO:OD=6:7$であり、 その$y$座標は負である。
点Eは線分AD上の点でAE=EDである。 さらに点Fは$x$軸上の点で、線分BFは$y$軸に平行である。 このとき次の問いに答えなさい。
①曲線②の式$y=ax^2$の$a$の値を求めなさい。
➁直線EFの式を求めなさい。
③線分AFと線分BOとの交点をGとするとき、三角形AGBと三角形DFGの曲積の比を最も簡単な整数の比で表しなさい。
投稿日:2018.10.27