 2次関数
2次関数
 2次関数
2次関数
【高校受験対策】数学-死守38

単元:
#数学(中学生)#中1数学#中2数学#中3数学#方程式#連立方程式#2次方程式#1次関数#確率#2次関数#円
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
高校受験対策・死守38
①$-7+5$を計算しなさい。
➁$\frac{3x-2}{5} \times10$を計算しなさい。
③$5ab^2 \div\frac{a}{3}$を計算しなさい。
④$(x+8)(x-6)$を計算しなさい。
⑤$25$の平方根を求めなさい。
⑥関数$y=\frac{a}{x}$のグラフが点$(6,-2)$を通るとき、$a$の値をを求めなさい。
⑦連立方程式を解きなさい。
$3x+y=-5$
$2x+3y=6$
⑧二次方程式を解きなさい。
$x^2+7x+1=0$
⑨右の図1で$\angle x$大きさを求めなさい。
⑩大小2つのさいころを同時に投げるとき、 2つとも同じ目が出る確率を求めなさい。
⑪右の図2において、点$A,B,C$は円$O$の周上の点である。
$\angle x$の大きさを求めなさい。
⑫左の図3のように、$y=ax^2(a\gt0)$のグラフ上 に2点$A,B$があり、$x$座標はそれぞれ$-6,4$である。
直線$AB$の傾きがであるとき、$a$の値を求めなさい。
この動画を見る
高校受験対策・死守38
①$-7+5$を計算しなさい。
➁$\frac{3x-2}{5} \times10$を計算しなさい。
③$5ab^2 \div\frac{a}{3}$を計算しなさい。
④$(x+8)(x-6)$を計算しなさい。
⑤$25$の平方根を求めなさい。
⑥関数$y=\frac{a}{x}$のグラフが点$(6,-2)$を通るとき、$a$の値をを求めなさい。
⑦連立方程式を解きなさい。
$3x+y=-5$
$2x+3y=6$
⑧二次方程式を解きなさい。
$x^2+7x+1=0$
⑨右の図1で$\angle x$大きさを求めなさい。
⑩大小2つのさいころを同時に投げるとき、 2つとも同じ目が出る確率を求めなさい。
⑪右の図2において、点$A,B,C$は円$O$の周上の点である。
$\angle x$の大きさを求めなさい。
⑫左の図3のように、$y=ax^2(a\gt0)$のグラフ上 に2点$A,B$があり、$x$座標はそれぞれ$-6,4$である。
直線$AB$の傾きがであるとき、$a$の値を求めなさい。
この問題一瞬で解ける?
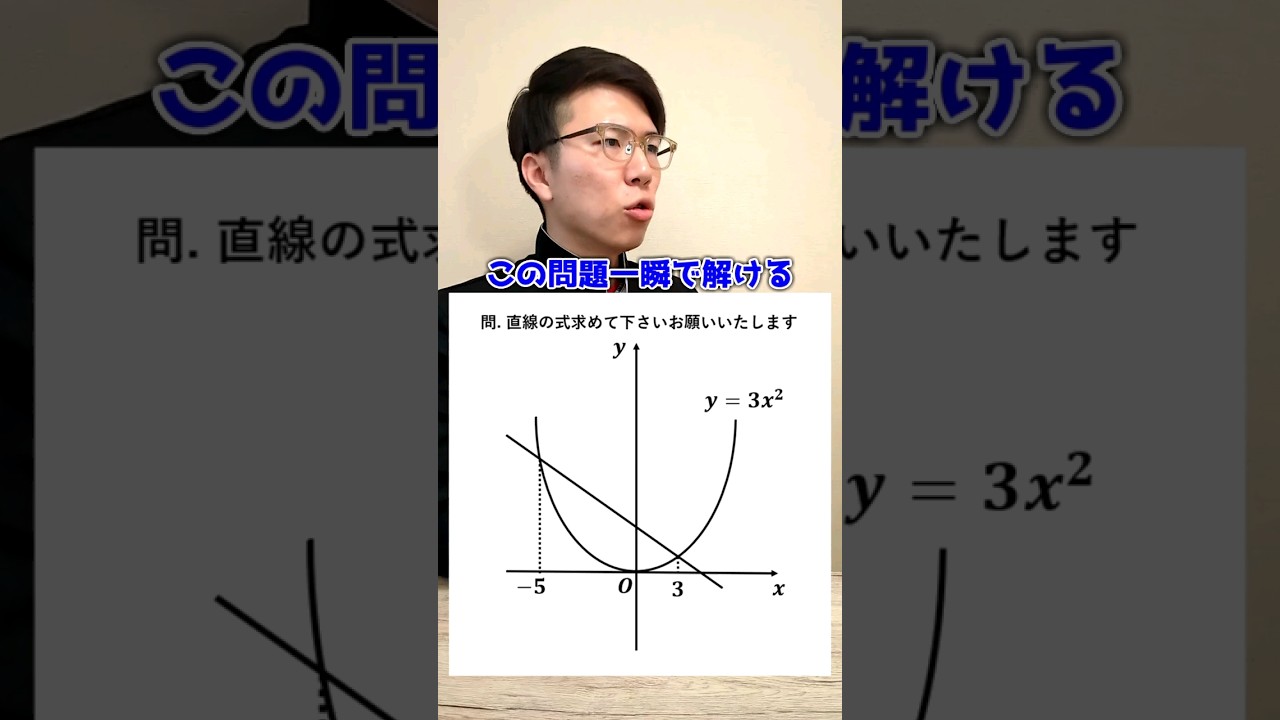
【イメージできるか…!】法政大学第二高等学校:二次関数~全国入試問題解法
単元:
#数学(中学生)#中3数学#2次関数#高校入試過去問(数学)#法政大学第二高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
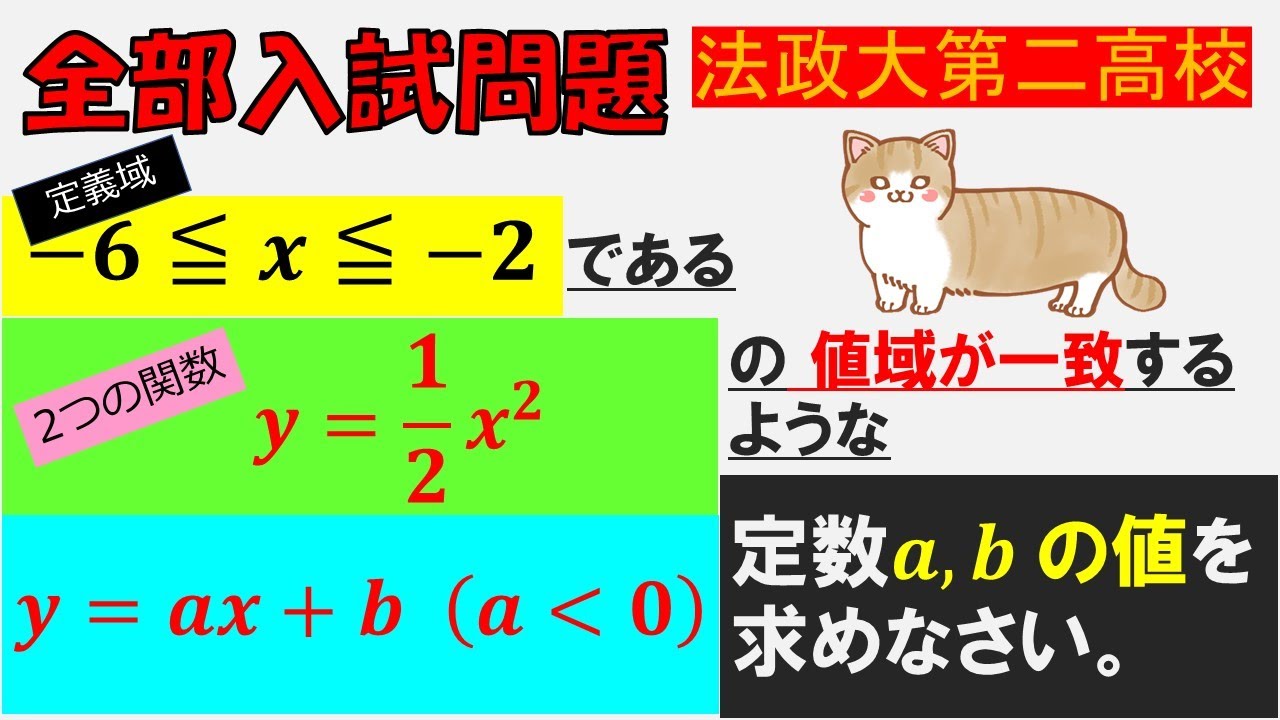
定義域$ -6 \leqq x \leqq -2 $である2つの関数
$ y=\dfrac{1}{2}x^2, y=ax+b(a \lt 0)$の値域が一致するような
定数$ a,b $の値を求めなさい.
法政大第二高校過去問
この動画を見る
定義域$ -6 \leqq x \leqq -2 $である2つの関数
$ y=\dfrac{1}{2}x^2, y=ax+b(a \lt 0)$の値域が一致するような
定数$ a,b $の値を求めなさい.
法政大第二高校過去問
【よく出題される…!】二次関数:和洋国府台女子高等学校~全国入試問題解法
単元:
#数学(中学生)#中3数学#2次関数
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
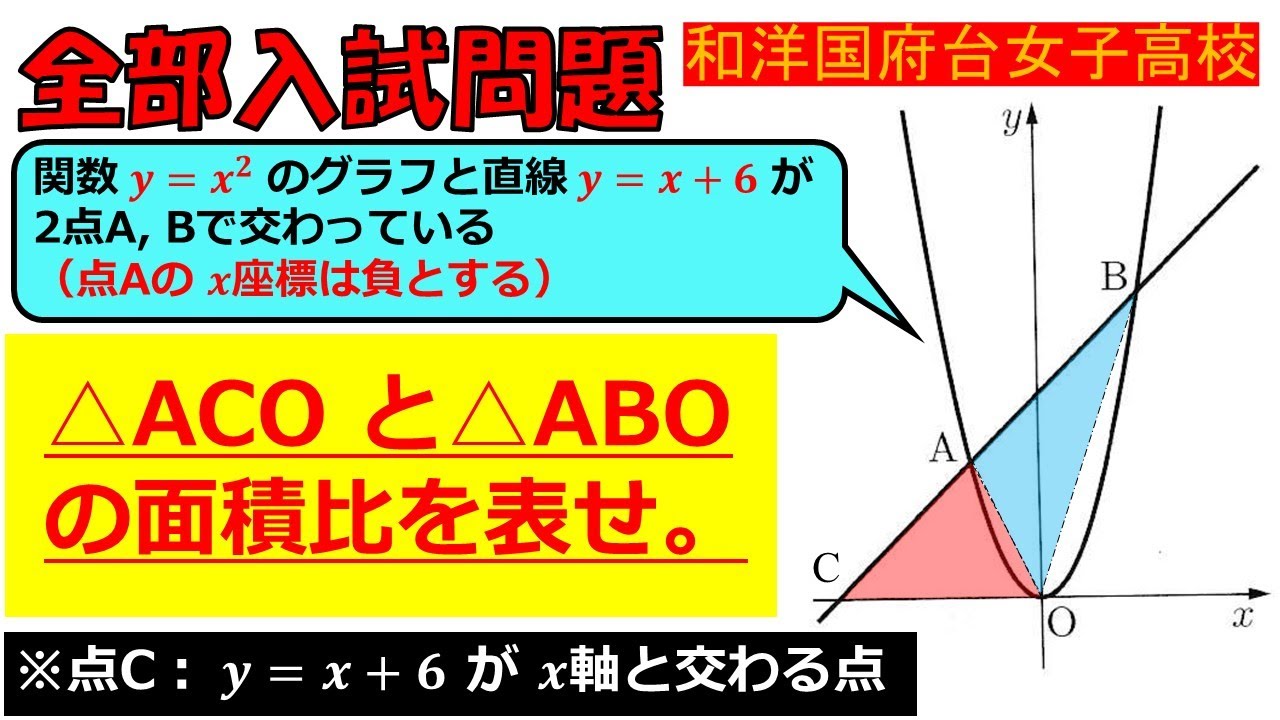
関数$ y=x^2 $のグラフと直線$ y=x+6 $が2点$ A,B $で交わっている.
(点Aのx座標は負とする)
$ \triangle ACO$ と$ \triangle ABO $の面積比を表せ.
和洋国府台女子高校過去問
この動画を見る
関数$ y=x^2 $のグラフと直線$ y=x+6 $が2点$ A,B $で交わっている.
(点Aのx座標は負とする)
$ \triangle ACO$ と$ \triangle ABO $の面積比を表せ.
和洋国府台女子高校過去問
数学好きな皆さまへ。解いてみて下さい

彼は何をしているのか?

グラフをかけ。

2023高校入試数学解説86問目 二次関数と変域の応用 埼玉県学校選択問題(改)

単元:
#数学(中学生)#中3数学#2次関数#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
$y=2x^2$についてxの変域が$a \leqq x \leqq a+4$のときyの変域は$0 \leqq y \leqq 18$となった。
aの値をすべて求めよ。
2023埼玉県
この動画を見る
$y=2x^2$についてxの変域が$a \leqq x \leqq a+4$のときyの変域は$0 \leqq y \leqq 18$となった。
aの値をすべて求めよ。
2023埼玉県
2023高校入試数学解説84問目 一次関数と二次関数 埼玉県学校選択問題
単元:
#数学(中学生)#中2数学#中3数学#1次関数#2次関数#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
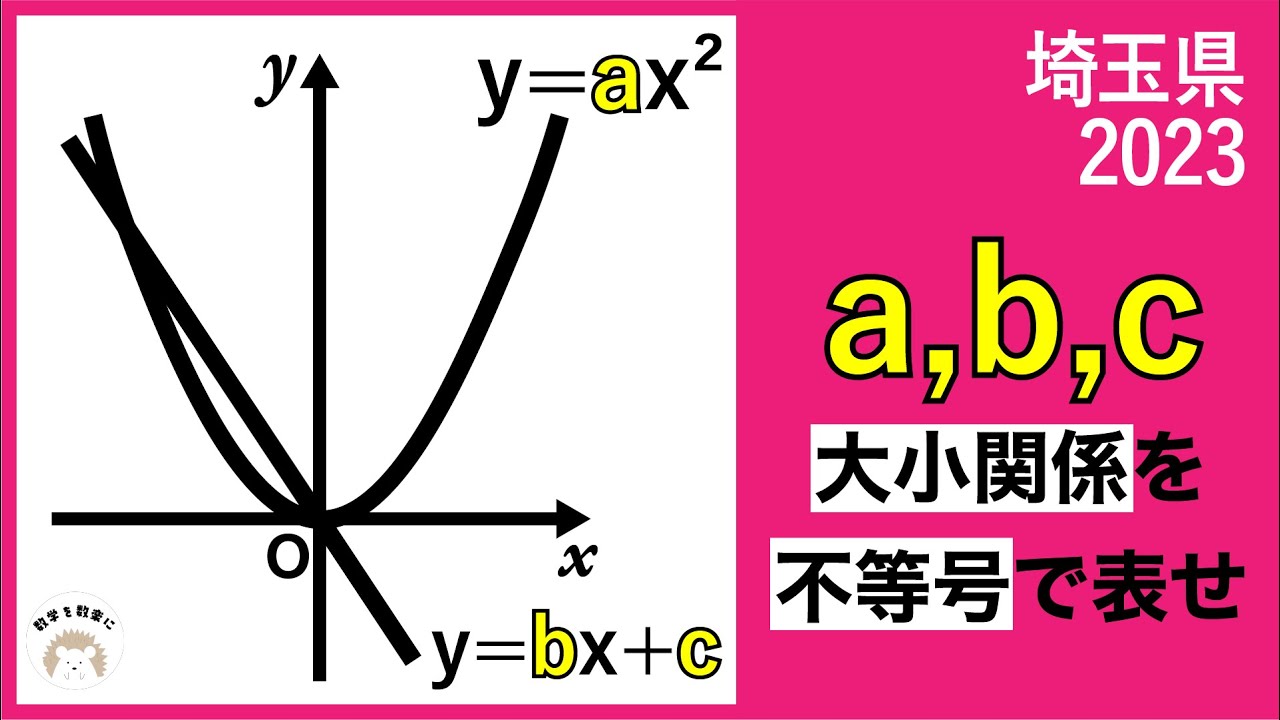
$y=ax^2$
$y=bx+c$
a,b,c大小関係を不等号で表せ
*図は動画内参照
2023埼玉県
この動画を見る
$y=ax^2$
$y=bx+c$
a,b,c大小関係を不等号で表せ
*図は動画内参照
2023埼玉県
2023高校入試数学解説81問目 二次関数の変域 埼玉県

単元:
#数学(中学生)#中3数学#2次関数#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
$y=2x^2$において
xの変域は$a \leqq x \leqq 1$
yの変域は$0 \leqq y \leqq 18$
aの値を求めよ
2023埼玉県
この動画を見る
$y=2x^2$において
xの変域は$a \leqq x \leqq 1$
yの変域は$0 \leqq y \leqq 18$
aの値を求めよ
2023埼玉県
2023高校入試数学解説71問目 2次関数の変域 千葉県

単元:
#数学(中学生)#中3数学#2次関数#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
$y= \frac{1}{3}x^2$において
xの変域は$-3 \leqq x \leqq a$
yの変域は$0 \leqq y \leqq 3$
整数aの値をすべて求めよ
2023千葉県
この動画を見る
$y= \frac{1}{3}x^2$において
xの変域は$-3 \leqq x \leqq a$
yの変域は$0 \leqq y \leqq 3$
整数aの値をすべて求めよ
2023千葉県
【短時間でマスター!!】2次関数のグラフの書き方を解説!〔現役塾講師解説、数学〕

単元:
#数学(中学生)#中3数学#数Ⅰ#2次関数#2次関数#2次関数とグラフ#数学(高校生)
指導講師:
3rd School
問題文全文(内容文):
数学1A
2次関数のグラフの書き方を解説します。
$y=x^2+2x-1$
①$-3≦x≦0$
②$0≦x≦2$の最大・最小
この動画を見る
数学1A
2次関数のグラフの書き方を解説します。
$y=x^2+2x-1$
①$-3≦x≦0$
②$0≦x≦2$の最大・最小
【短時間で各パターン解説!!】2次関数の変域の基礎を現役塾講師が簡単に解説!〔現役塾講師解説、数学〕

単元:
#数学(中学生)#中3数学#2次関数
指導講師:
3rd School
問題文全文(内容文):
中学3年生 数学
二次関数の変域
$y=2x^2$について、$1≦x≦5$のとき$y$の変域は?
$y=x^2$について、$-3≦x≦2$のとき$y$の変域は?
$y=-2x^2$について、$-4≦x≦2$のとき$y$の変域は?
この動画を見る
中学3年生 数学
二次関数の変域
$y=2x^2$について、$1≦x≦5$のとき$y$の変域は?
$y=x^2$について、$-3≦x≦2$のとき$y$の変域は?
$y=-2x^2$について、$-4≦x≦2$のとき$y$の変域は?
【中学数学】2次関数の変化の割合~どこよりも丁寧に~ 4-3【中3数学】

単元:
#数学(中学生)#中3数学#2次関数
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
2次関数の変化の割合
(例題1)$y=x^2$でxの値が1から5まで増加するときの変化の割合を求めよ。
(例題2)$y=x^2$でxの値が-1から2まで増加するときの変化の割合を求めよ。
この動画を見る
2次関数の変化の割合
(例題1)$y=x^2$でxの値が1から5まで増加するときの変化の割合を求めよ。
(例題2)$y=x^2$でxの値が-1から2まで増加するときの変化の割合を求めよ。
【中学数学】2次関数の決定~変域~ 4-2.5【中3数学】

単元:
#数学(中学生)#中3数学#2次関数
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
関数 $y=ax^2$で$x$の変域が$-1 \leqq x \leqq 6$のとき、$y$の変域が$-18 \leqq y \leqq 0$である。このときの$a$を求めよ。
この動画を見る
関数 $y=ax^2$で$x$の変域が$-1 \leqq x \leqq 6$のとき、$y$の変域が$-18 \leqq y \leqq 0$である。このときの$a$を求めよ。
【中学数学】2次関数の変域をどこよりも丁寧に 4-2【中3数学】

【数検3級】数学検定3級2次 問題7

単元:
#数学(中学生)#中3数学#数学検定・数学甲子園・数学オリンピック等#2次関数#数学検定#数学検定3級
指導講師:
理数個別チャンネル
問題文全文(内容文):
問題7.右の図のように、関数$y=ax^2$のグラフ上に、2点A、Bをとります。点Aの座標を(4,8)で、点Bのx座標は-3です。
次の問いに答えなさい。
(15) aの値を求めなさい。この問題は、計算の途中の式と答えを書きなさい。
(16) 点B の座標を求めなさい。
(17) xの変域が$-3\leqq x\leqq 4$のときのyの変域を求めなさい。
この動画を見る
問題7.右の図のように、関数$y=ax^2$のグラフ上に、2点A、Bをとります。点Aの座標を(4,8)で、点Bのx座標は-3です。
次の問いに答えなさい。
(15) aの値を求めなさい。この問題は、計算の途中の式と答えを書きなさい。
(16) 点B の座標を求めなさい。
(17) xの変域が$-3\leqq x\leqq 4$のときのyの変域を求めなさい。
関数って結局なんなん?

単元:
#数学(中学生)#中2数学#中3数学#1次関数#2次関数
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
関数についての動画です。
例にとっているのは比例ですが,一次関数,二次関数,三次関数になっても考え方は同じです。
この動画を見る
関数についての動画です。
例にとっているのは比例ですが,一次関数,二次関数,三次関数になっても考え方は同じです。
【保存版】2次関数上の直線の式を一瞬で出す方法

2次関数のの裏技

座標平面上の直角三角形 立教新座
単元:
#数学(中学生)#中3数学#数A#図形の性質#2次関数#三角形の辺の比(内分・外分・二等分線)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
△AOBが直角三角形になるときのaの値を全て求めよ。
*図は動画内参照
立教新座高等学校
この動画を見る
△AOBが直角三角形になるときのaの値を全て求めよ。
*図は動画内参照
立教新座高等学校
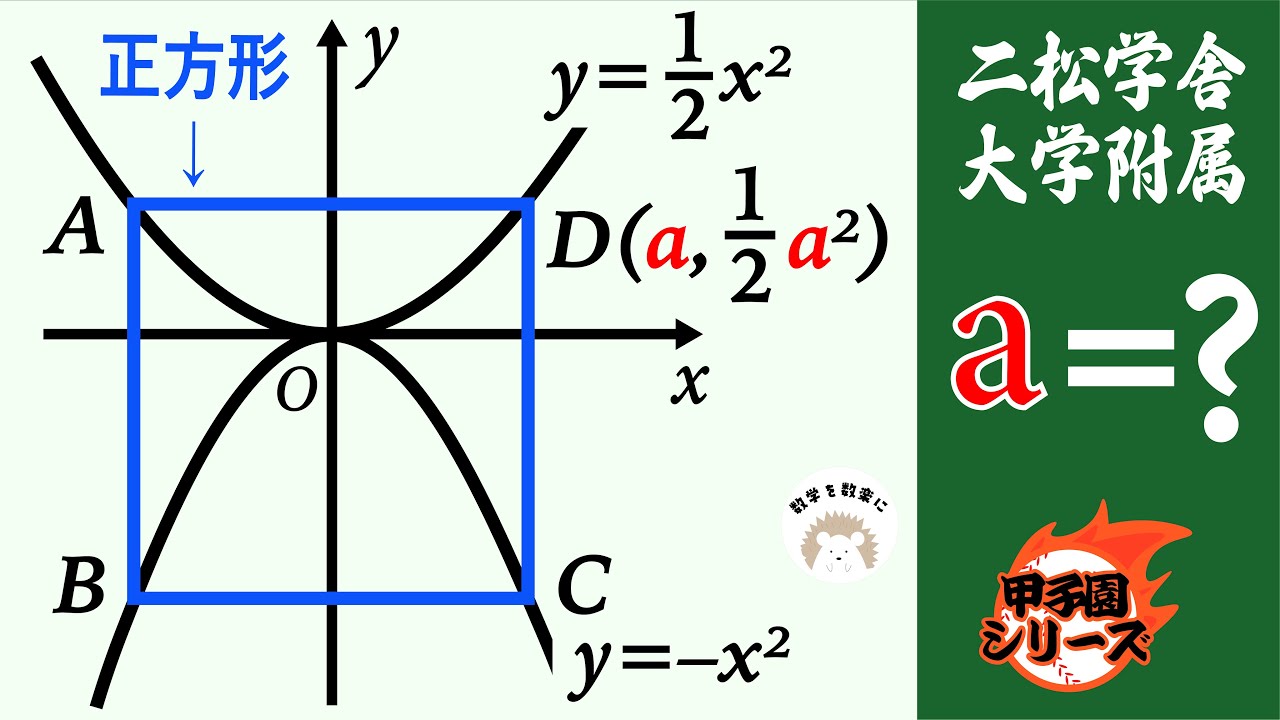
放物線と正方形 二松学舎大附属
二次関数の変域 天理高校

単元:
#数学(中学生)#中3数学#2次関数#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
$y=x^2$
xの変域が$a \leqq x \leqq 2$のとき
yの変域が$0 \leqq y \leqq 4$となる
aの値の範囲は?
天理高等学校
この動画を見る
$y=x^2$
xの変域が$a \leqq x \leqq 2$のとき
yの変域が$0 \leqq y \leqq 4$となる
aの値の範囲は?
天理高等学校
やる気を出して動体視力と数学を鍛える動画~全国入試問題解法

単元:
#数学(中学生)#中3数学#2次関数#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
関数$y=2x^2$の$y$の変域が$-2\leqq x\leqq a$のとき,
$y$の変域が$b\leqq y\leqq 18$である.
$a,b$の値を求めなさい.
函館ラサール高校過去問
この動画を見る
関数$y=2x^2$の$y$の変域が$-2\leqq x\leqq a$のとき,
$y$の変域が$b\leqq y\leqq 18$である.
$a,b$の値を求めなさい.
函館ラサール高校過去問
動体視力と数学を鍛えるTik tok~全国入試問題解法 #Shorts

単元:
#数学(中学生)#中3数学#2次関数#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
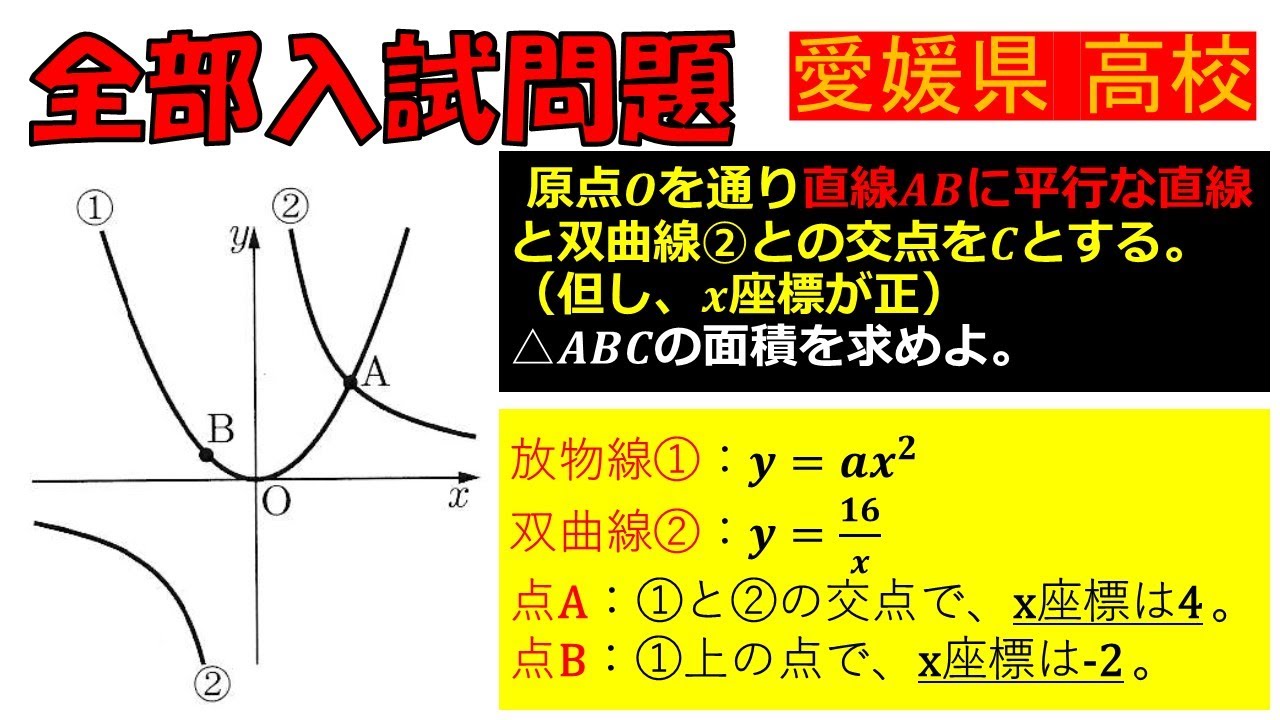
原点$O$を通り直線$AB$に平行な直線と双曲線②との交点を$C$とする.(但し,$x$座標が正)
$\triangle ABC$の面積を求めよ.
愛媛県高校過去問
この動画を見る
原点$O$を通り直線$AB$に平行な直線と双曲線②との交点を$C$とする.(但し,$x$座標が正)
$\triangle ABC$の面積を求めよ.
愛媛県高校過去問
【整数問題?座標問題?】二次関数:名古屋女子大学高等学校~全国入試問題解法
単元:
#数学(中学生)#中3数学#2次関数#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
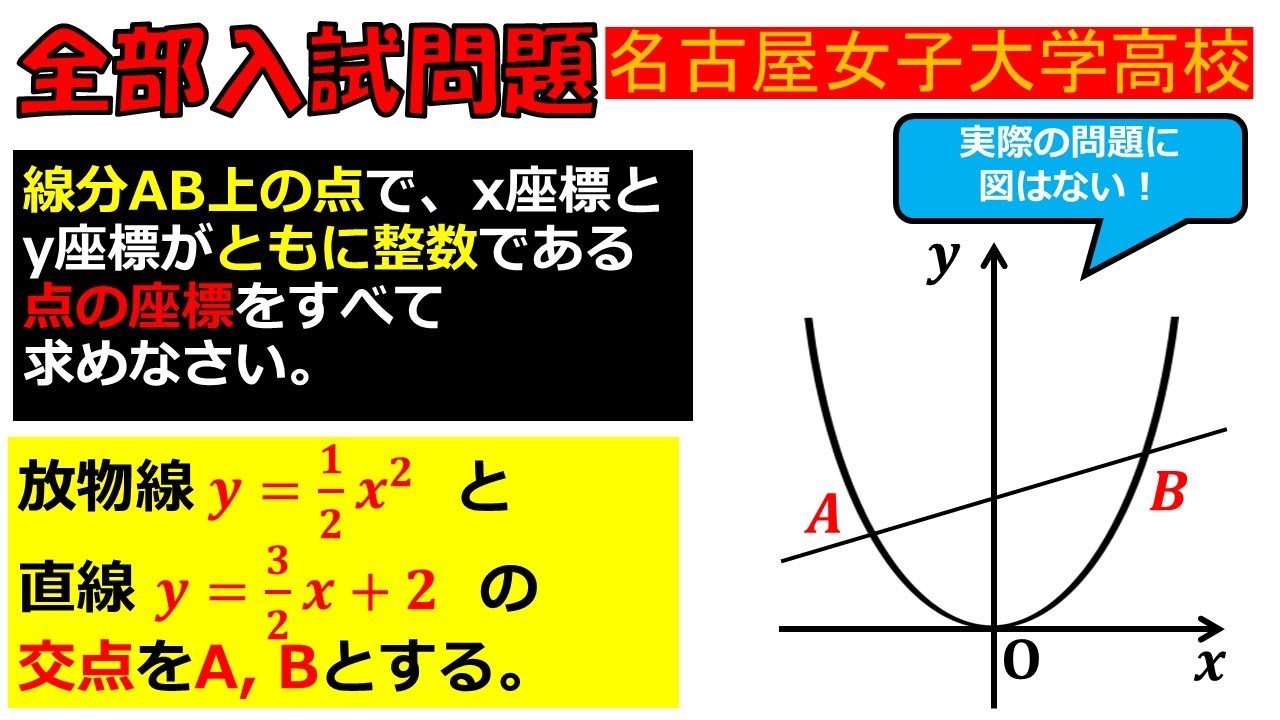
放物線$y=\dfrac{1}{2}x^2$と直線$y=\dfrac{3}{2}x+2$の交点を$A,B$とする.
線分$AB$上の点で,$x$座標と$y$座標がともに整数である点の座標をすべて求めなさい.
名古屋女子大学高等学校過去問
この動画を見る
放物線$y=\dfrac{1}{2}x^2$と直線$y=\dfrac{3}{2}x+2$の交点を$A,B$とする.
線分$AB$上の点で,$x$座標と$y$座標がともに整数である点の座標をすべて求めなさい.
名古屋女子大学高等学校過去問
動体視力とYouTubeのAIを確認する数学~全国入試問題解法 #Shorts

単元:
#数学(中学生)#中3数学#2次関数#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
図の曲線は関数$y=x^2$である.
曲線上に$x$座標が$-3,2$である2点$A$と$B$である.
2点$A,B$を通る直線$l$があり,$l$と$x$軸の交点を$C$とする.
$\triangle AOC$の面積を求めなさい.
埼玉県高校過去問
この動画を見る
図の曲線は関数$y=x^2$である.
曲線上に$x$座標が$-3,2$である2点$A$と$B$である.
2点$A,B$を通る直線$l$があり,$l$と$x$軸の交点を$C$とする.
$\triangle AOC$の面積を求めなさい.
埼玉県高校過去問
二次関数の変域 応用 専修大学松戸 令和4年度 2022 入試問題100題解説96問目!

単元:
#数学(中学生)#中3数学#2次関数#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
$y= \frac{1}{3}x^2$について
$-a-2 \leqq x \leqq a$のとき $0 \leqq y \leqq 27$
a=?
2022専修大学松戸高等学校
この動画を見る
$y= \frac{1}{3}x^2$について
$-a-2 \leqq x \leqq a$のとき $0 \leqq y \leqq 27$
a=?
2022専修大学松戸高等学校
【見通しを立てて、素早く解こう!】二次関数:愛媛県公立高等学校~全国入試問題解法
単元:
#数学(中学生)#中3数学#2次関数#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
原点$O$を通り直線$AB$に平行な直線と双曲線②との交点を$C$とする.(但し,$x$座標が正)
$\triangle ABC$の面積を求めよ.
愛媛県高校過去問
この動画を見る
原点$O$を通り直線$AB$に平行な直線と双曲線②との交点を$C$とする.(但し,$x$座標が正)
$\triangle ABC$の面積を求めよ.
愛媛県高校過去問
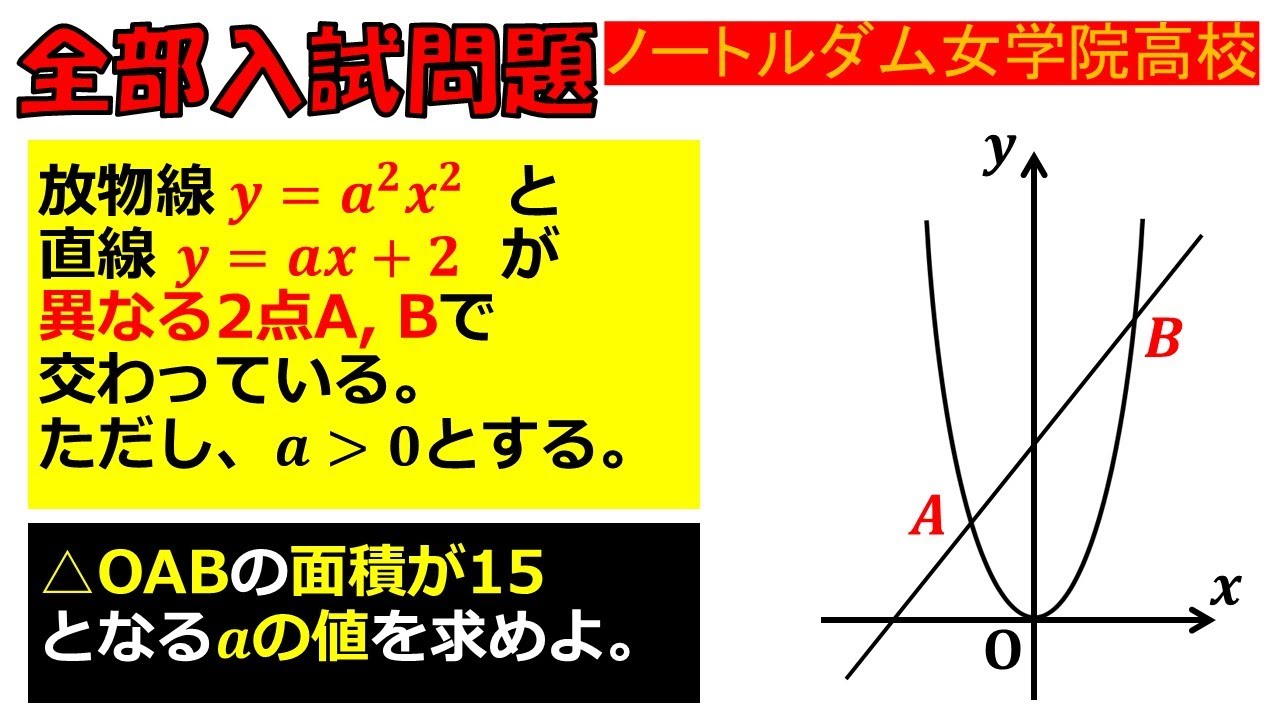
【発展のために一度は解いておきたい!】二次関数:ノートルダム女学院高等学校~全国入試問題解法
単元:
#数学(中学生)#中3数学#2次関数#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
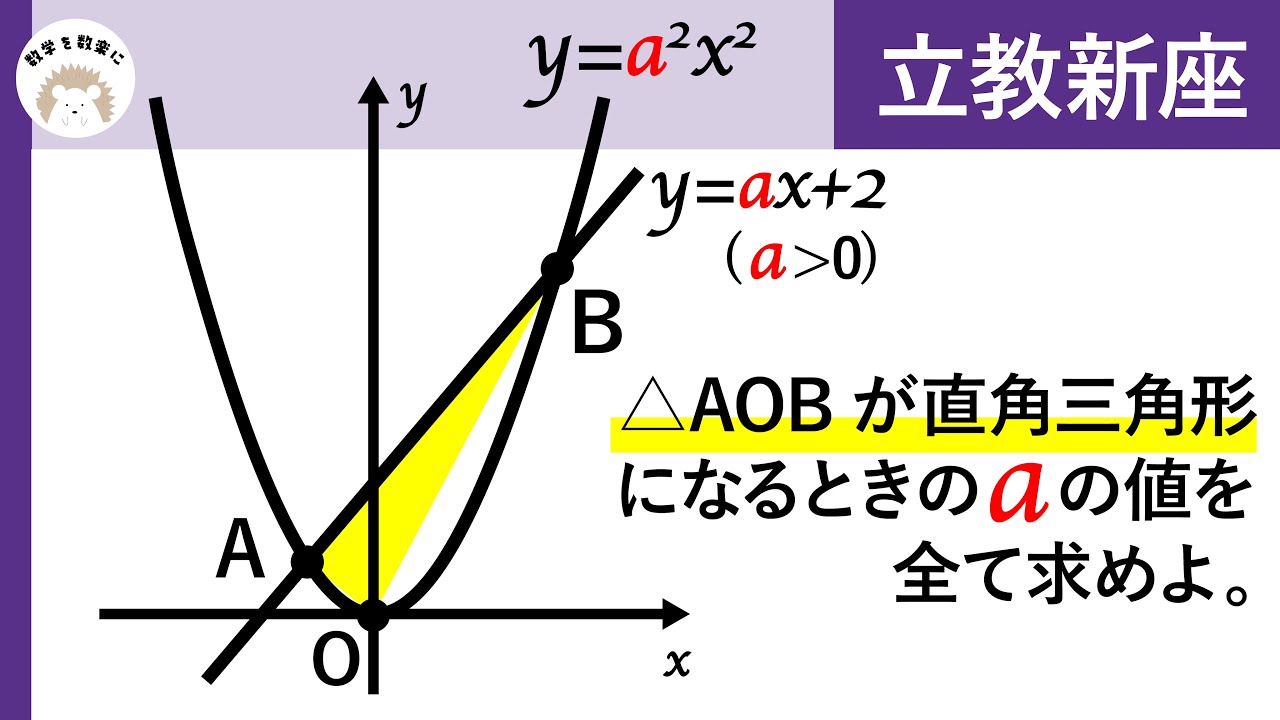
放物線$y=a^2x^2$と直線$y=ax+2$が異なる2点$A,B$で交わっている.
ただし,$a\gt 0$とする.
$\triangle OAB$の面積が$15$となる$a$の値を求めよ.
ノートルダム女学院高校過去問
この動画を見る
放物線$y=a^2x^2$と直線$y=ax+2$が異なる2点$A,B$で交わっている.
ただし,$a\gt 0$とする.
$\triangle OAB$の面積が$15$となる$a$の値を求めよ.
ノートルダム女学院高校過去問
