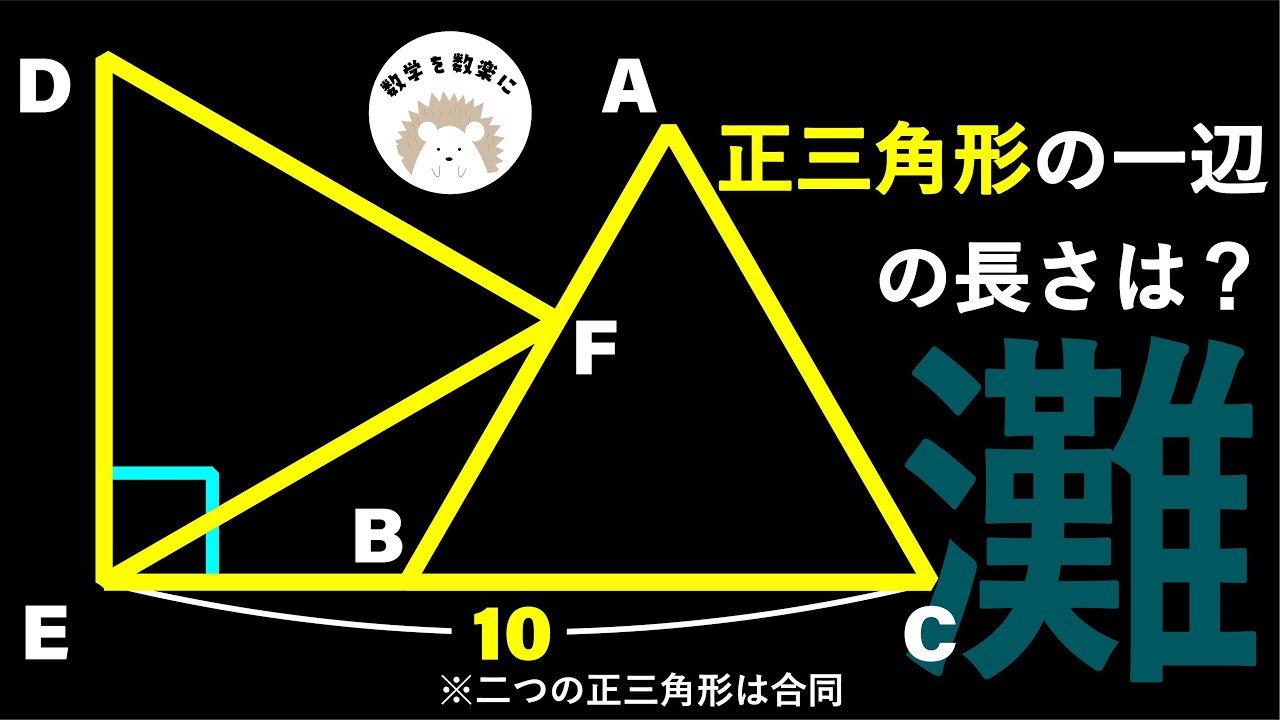
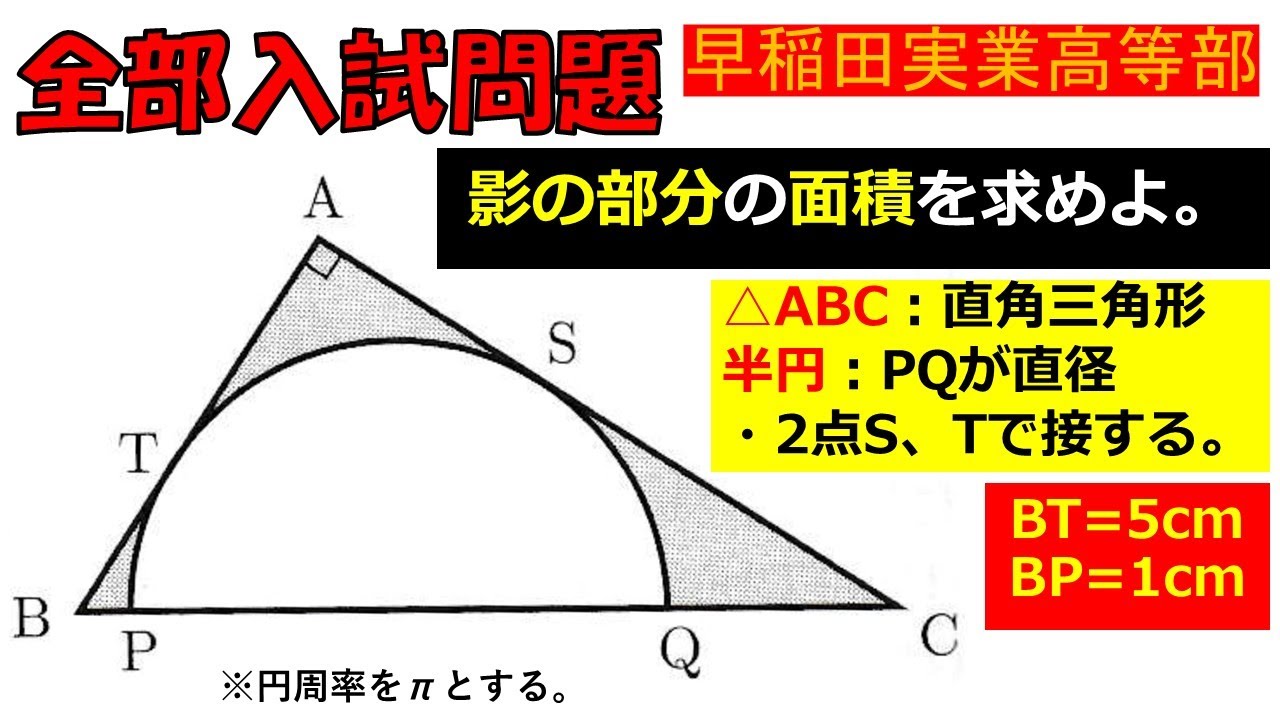
問題文全文(内容文)：
高校受験対策・図形28

Q
右の図1で、四角形$ABCD$は平行四辺形である。
点$P$は辺$CD$上にある点で、頂点$C$,頂点$D$のいずれにも一致しない。頂点$A$と点$P$を結ぶ。

問1
図1において、$\angle ABC=50°$、$\angle DAP$の大きさを$a°$とするとき、
$\angle APC$の大きさを$a$を用いて表しなさい。

問2
右の図2は、図1において頂点$B$と点$P$を結び、頂点$D$を通り線分$BP$に平行な直線を引き、
辺$AB$との交点を$Q$、線分$AP$との交点を$R$とする。 次の(1)、(2)に答えよ。

(1) $\triangle ABP \backsim \triangle PDR$であることを証明せよ。

(2) 図2において頂点$C$と点$R$を結び、線分$BP$と線分$CR$の交点を$S$とする。
$CP:PD=2:1$のとき、四角に$QBSR$の面積は$△AQR$の面積の何倍であるが求めなさい。