生徒からの質問３ きつね形の角度は？ - 質問解決D.B.（データベース）
Generic selectors
完全一致検索
タイトルから検索
記事本文から検索
Post Type Selectors
all_unit_post
質問解決D.B.（データベース） > 動画投稿 > 算数(中学受験) > 平面図形 > 角度と面積 > 生徒からの質問３　きつね形の角度は？

生徒からの質問３　きつね形の角度は？

問題文全文(内容文)：
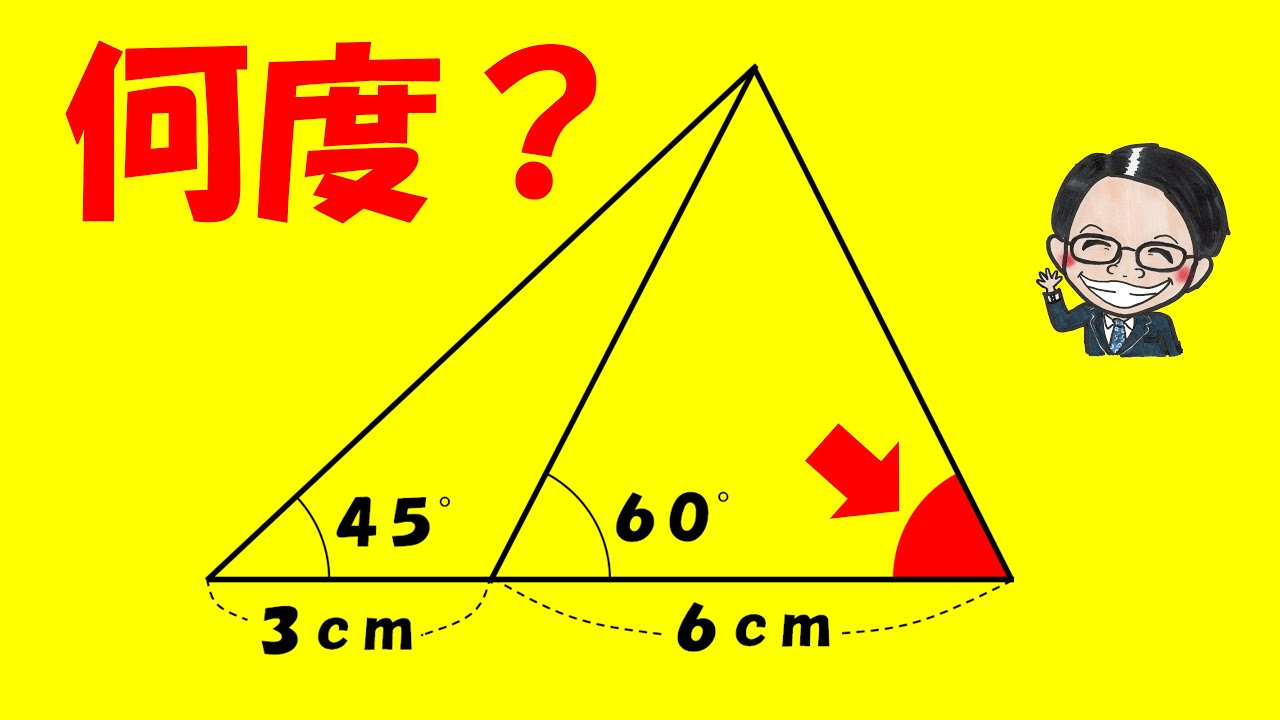
$図中xの角度は？$
(図は動画を参照)
チャプター：

0:00 導入
0:20　問題解答に必要な基礎知識　三角形の内角と外角の関係
0:53　きつね形の角度計算　やり方解説
3:33　キツネ形の角度計算　裏技紹介

単元： #算数(中学受験)#平面図形#角度と面積
指導講師： こばちゃん塾
問題文全文(内容文)：
$図中xの角度は？$
(図は動画を参照)
投稿日：2020.03.13

＜関連動画＞

【中学受験問題に挑戦】141（”大人”は頭の体操）　三角形と四角形の考察

アイキャッチ画像
単元： #算数(中学受験)#平面図形#角度と面積
指導講師： 算数・数学ちゃんねる
問題文全文(内容文)：
長方形の中には図形がある。
〇は線ABを5等分する。
色ある部分の面積は？
この動画を見る　

フェリス女学院中学校2023年算数「数の規則性」解説

アイキャッチ画像
単元： #算数(中学受験)#計算と数の性質#過去問解説(学校別)#規則性（周期算・方陣算・数列・日暦算・N進法）#フェリス女学院中学
指導講師： 重吉
問題文全文(内容文)：
フェリス女学院中学校2023年算数「数の規則性」
ラムネを3本買うと空き瓶3本で1本もらえます
①ラムネを30本買って交換してもらうと、合計で何本飲めるか求めよ
②100本飲むには何本買えばいいか求めよ
この動画を見る　

あなたはイケてる解き方にたどり着ける？実は超簡単に解ける方法あるんです！！【中学受験算数】【鎌倉学園中学校】

アイキャッチ画像
単元： #算数(中学受験)#平面図形#角度と面積
指導講師： こばちゃん塾
問題文全文(内容文)：
・左図のように、半径が2㎝の大きい円の中に、同じ大きさの小さい円を8つかいた。
斜線部分の面積は？
（円周率は3.14）

＊図は動画内参照
この動画を見る　

○○に気づけば一瞬で解ける！？実は簡単なんです！【中学受験算数】

アイキャッチ画像
単元： #平面図形#角度と面積
指導講師： こばちゃん塾
問題文全文(内容文)：
正方形ABCD内の三角形ABEの面積は？
＊図は動画内参照
この動画を見る　

あの形に気づけるかな？難問だけど超スッキリ解ける一題！【中学受験算数】【難問】

アイキャッチ画像
単元： #算数(中学受験)#平面図形#平面図形その他
指導講師： こばちゃん塾
問題文全文(内容文)：
下の長方形ABCDでxは何㎝？
＊図は動画内参照
この動画を見る　
PAGE TOP