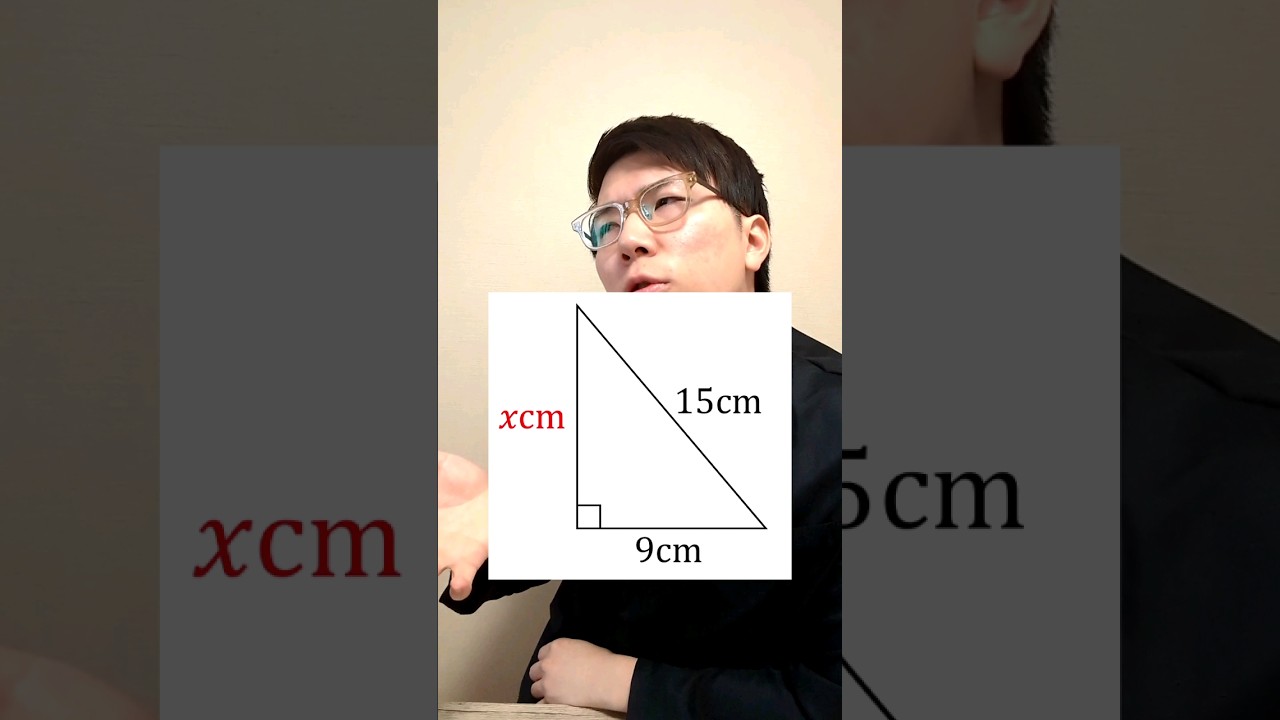
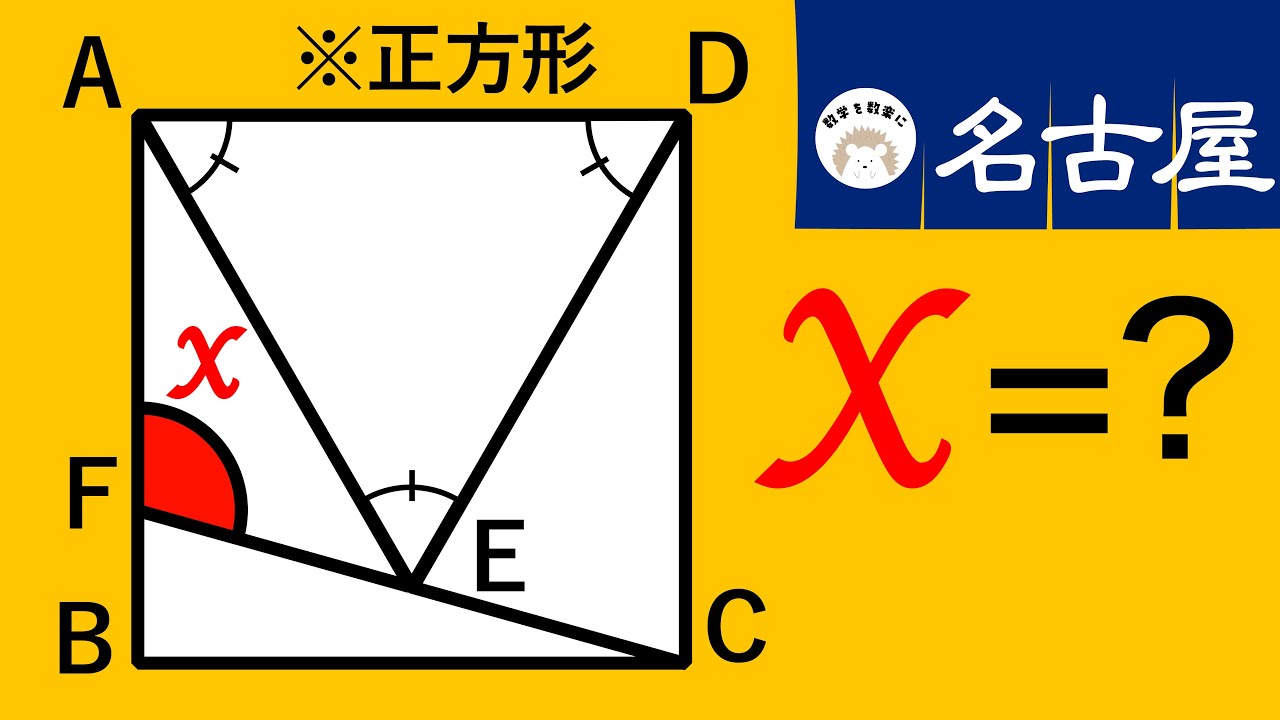
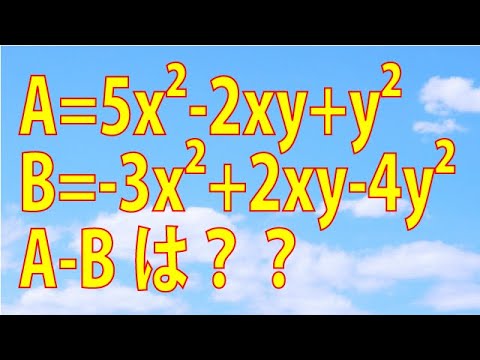問題文全文(内容文):
◎傾きと切片はいくつ?(傾・切)
①$y=-4$→( ・ )
②$y=-x+5$→( ・ )
◎右の③~⑧について$\boxed{A}~\boxed{F}$の中からあてはまるものを書こう!
$\boxed{A} y=-\displaystyle \frac{1}{2}+3$
$\boxed{B} y=-3x+1$
$\boxed{C} y=-2x+4$
$\boxed{D} y=\displaystyle \frac{1}{2}x+4$
$\boxed{E} y=-3x+18$
$\boxed{F} y=x-5$
③(3,-2)を通るのは?
④平行なのはどれとどれ?
⑤(0.4)を通るのは?
⑥右上がりなのは?
⑦xが増加するとき、yは減少するのは?
◎傾きと切片はいくつ?(傾・切)
①$y=-4$→( ・ )
②$y=-x+5$→( ・ )
◎右の③~⑧について$\boxed{A}~\boxed{F}$の中からあてはまるものを書こう!
$\boxed{A} y=-\displaystyle \frac{1}{2}+3$
$\boxed{B} y=-3x+1$
$\boxed{C} y=-2x+4$
$\boxed{D} y=\displaystyle \frac{1}{2}x+4$
$\boxed{E} y=-3x+18$
$\boxed{F} y=x-5$
③(3,-2)を通るのは?
④平行なのはどれとどれ?
⑤(0.4)を通るのは?
⑥右上がりなのは?
⑦xが増加するとき、yは減少するのは?
単元:
#中2数学#中3数学#1次関数
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
◎傾きと切片はいくつ?(傾・切)
①$y=-4$→( ・ )
②$y=-x+5$→( ・ )
◎右の③~⑧について$\boxed{A}~\boxed{F}$の中からあてはまるものを書こう!
$\boxed{A} y=-\displaystyle \frac{1}{2}+3$
$\boxed{B} y=-3x+1$
$\boxed{C} y=-2x+4$
$\boxed{D} y=\displaystyle \frac{1}{2}x+4$
$\boxed{E} y=-3x+18$
$\boxed{F} y=x-5$
③(3,-2)を通るのは?
④平行なのはどれとどれ?
⑤(0.4)を通るのは?
⑥右上がりなのは?
⑦xが増加するとき、yは減少するのは?
◎傾きと切片はいくつ?(傾・切)
①$y=-4$→( ・ )
②$y=-x+5$→( ・ )
◎右の③~⑧について$\boxed{A}~\boxed{F}$の中からあてはまるものを書こう!
$\boxed{A} y=-\displaystyle \frac{1}{2}+3$
$\boxed{B} y=-3x+1$
$\boxed{C} y=-2x+4$
$\boxed{D} y=\displaystyle \frac{1}{2}x+4$
$\boxed{E} y=-3x+18$
$\boxed{F} y=x-5$
③(3,-2)を通るのは?
④平行なのはどれとどれ?
⑤(0.4)を通るのは?
⑥右上がりなのは?
⑦xが増加するとき、yは減少するのは?
投稿日:2013.07.21