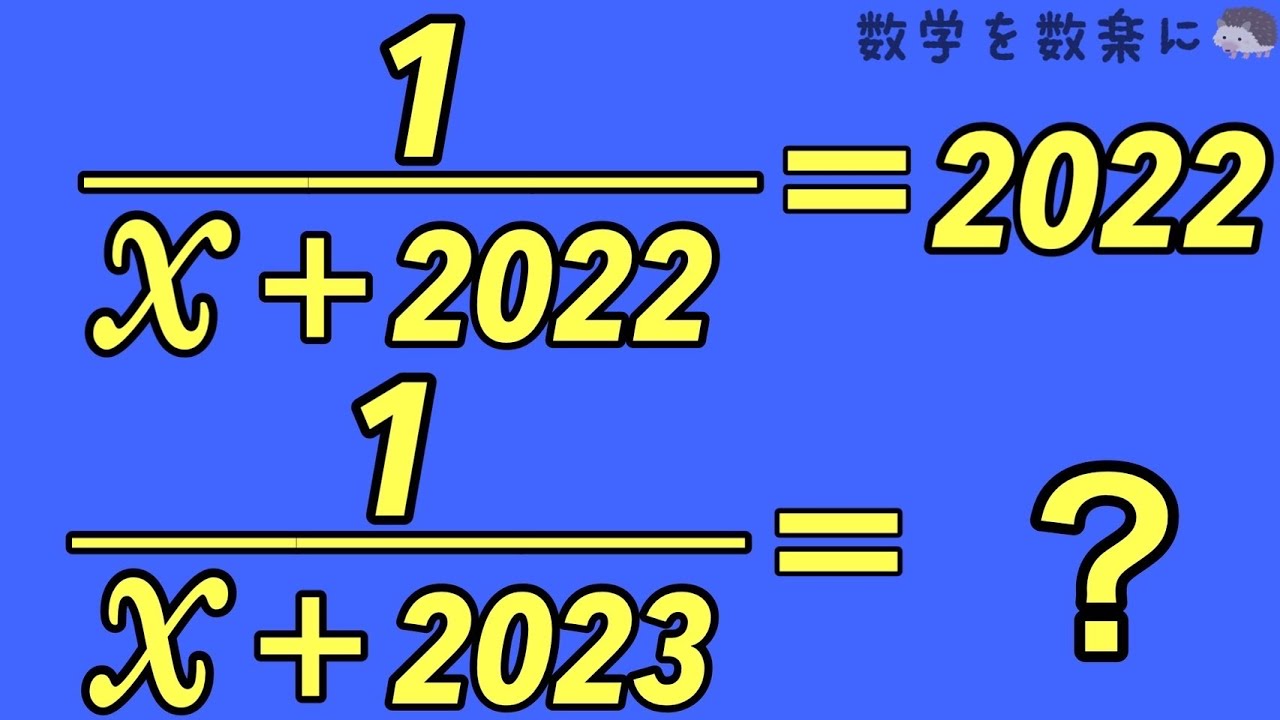問題文全文(内容文):
$
\begin{eqnarray}
\left\{
\begin{array}{l}
x + y = m \\
x-y = n
\end{array}
\right.
\end{eqnarray}
$
のとき素数x,y,m,nを求めよ。
早稲田大学高等学院
$
\begin{eqnarray}
\left\{
\begin{array}{l}
x + y = m \\
x-y = n
\end{array}
\right.
\end{eqnarray}
$
のとき素数x,y,m,nを求めよ。
早稲田大学高等学院
単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
$
\begin{eqnarray}
\left\{
\begin{array}{l}
x + y = m \\
x-y = n
\end{array}
\right.
\end{eqnarray}
$
のとき素数x,y,m,nを求めよ。
早稲田大学高等学院
$
\begin{eqnarray}
\left\{
\begin{array}{l}
x + y = m \\
x-y = n
\end{array}
\right.
\end{eqnarray}
$
のとき素数x,y,m,nを求めよ。
早稲田大学高等学院
投稿日:2021.09.23