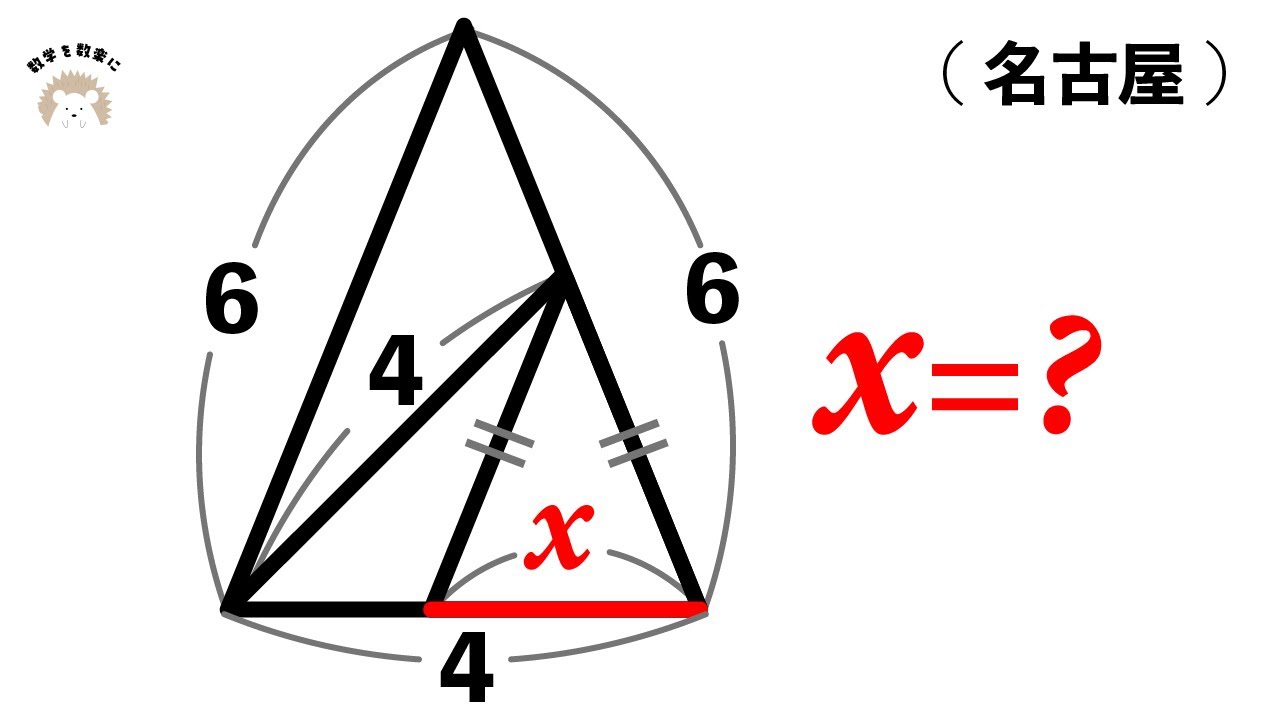
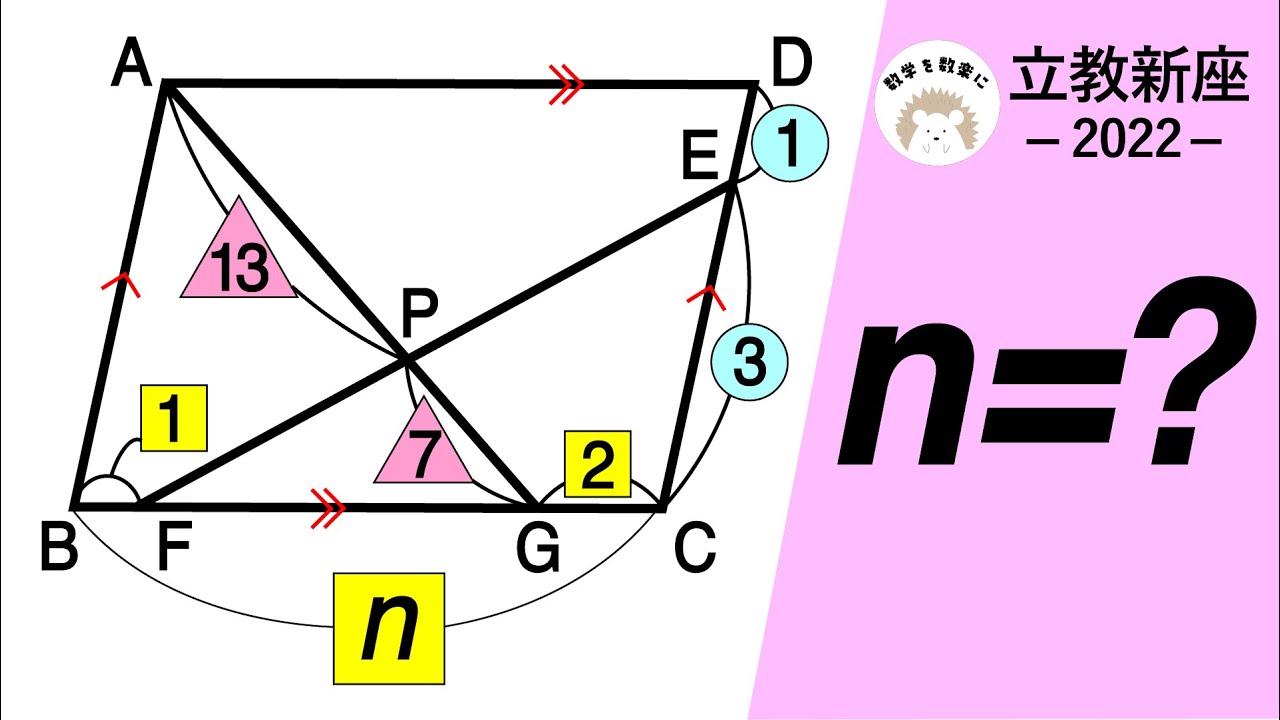
問題文全文(内容文):
$ n $は正の整数であり, $ a,b,c,d $は整数である.
$ n=(a^2-1)(b^2-2)\times(c^2-3)(d^2-4)$
このような$ \color{red}{nの値}$で最小の値は$ \Box $である.
福岡大学附属大濠高等学校過去問
$ n $は正の整数であり, $ a,b,c,d $は整数である.
$ n=(a^2-1)(b^2-2)\times(c^2-3)(d^2-4)$
このような$ \color{red}{nの値}$で最小の値は$ \Box $である.
福岡大学附属大濠高等学校過去問
単元:
#数学(中学生)#中1数学#文字と式#高校入試過去問(数学)#福岡大学附属大濠高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$ n $は正の整数であり, $ a,b,c,d $は整数である.
$ n=(a^2-1)(b^2-2)\times(c^2-3)(d^2-4)$
このような$ \color{red}{nの値}$で最小の値は$ \Box $である.
福岡大学附属大濠高等学校過去問
$ n $は正の整数であり, $ a,b,c,d $は整数である.
$ n=(a^2-1)(b^2-2)\times(c^2-3)(d^2-4)$
このような$ \color{red}{nの値}$で最小の値は$ \Box $である.
福岡大学附属大濠高等学校過去問
投稿日:2023.10.16