三つ子素数

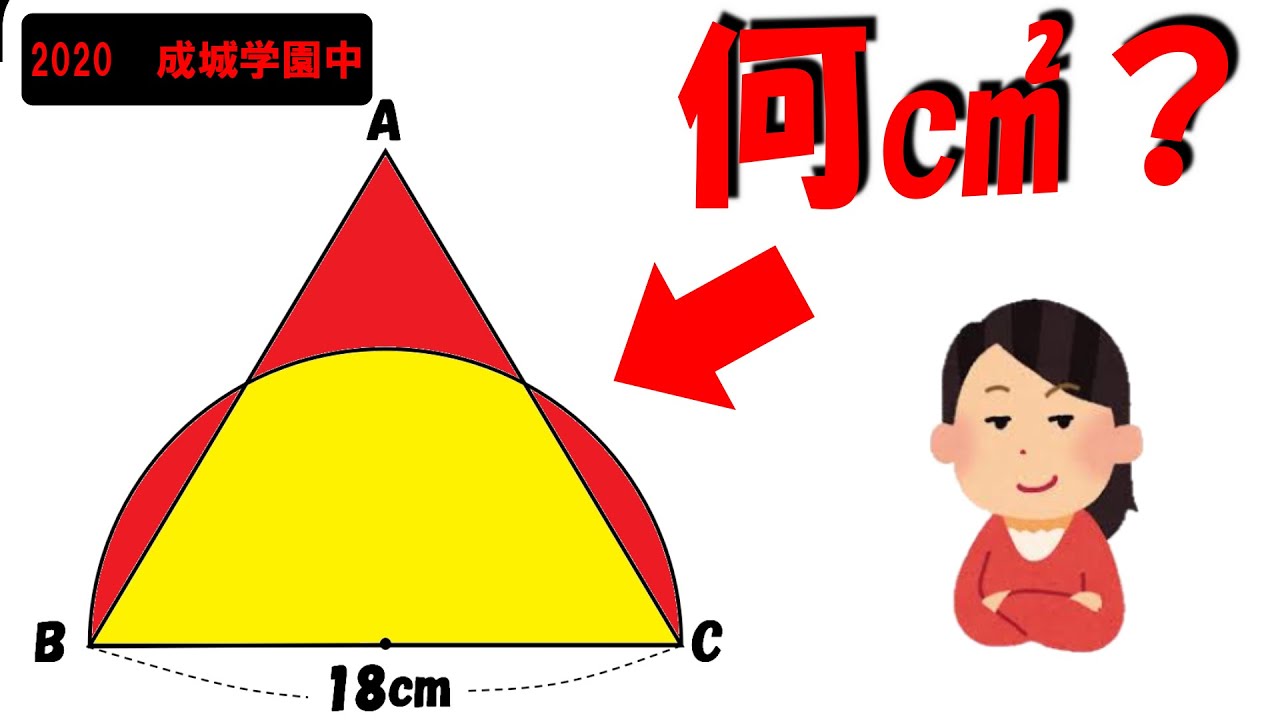
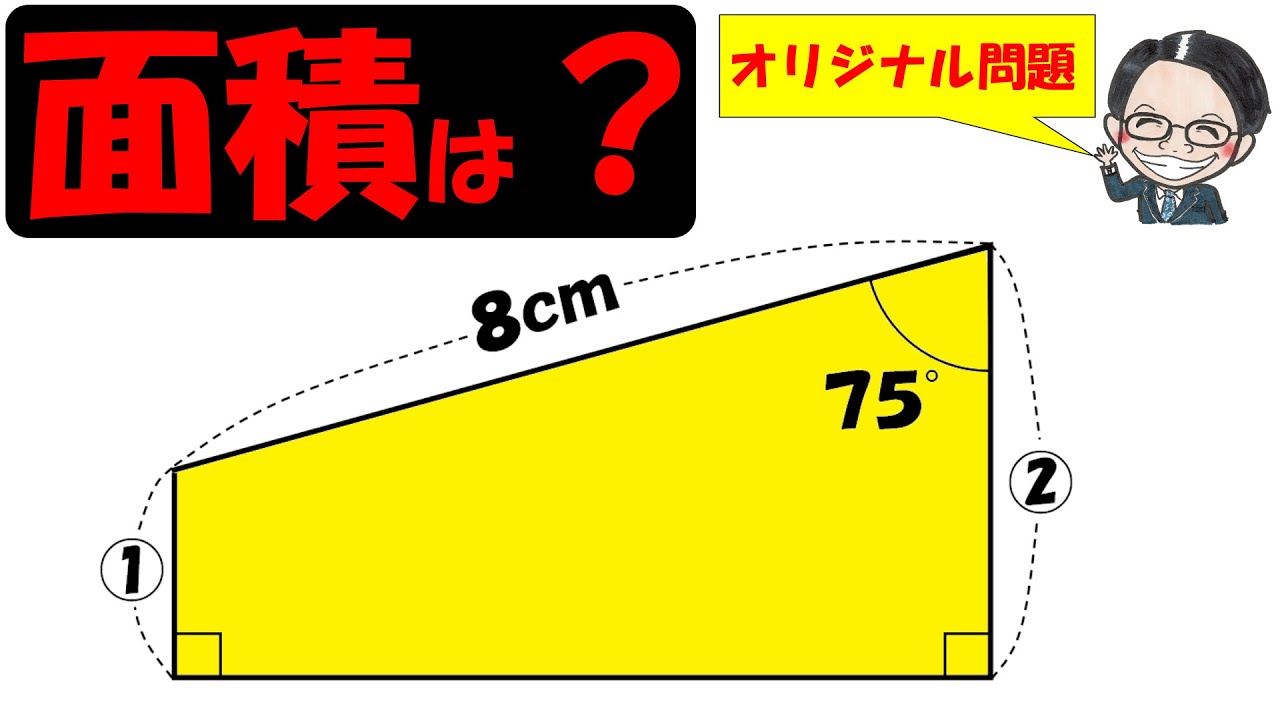
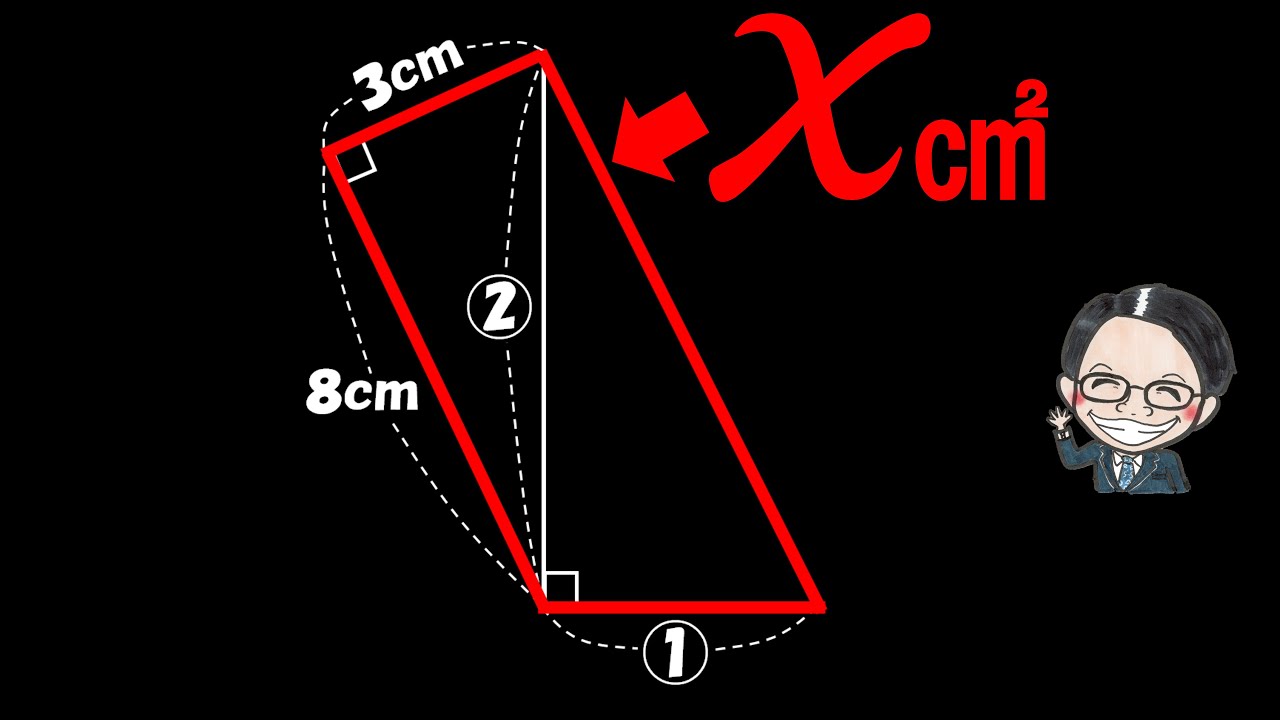
問題文全文(内容文)：
P,P+2,P+4が全て素数のとき、3つ子素数という。
3つ子素数をすべて求めよ。

単元： #算数(中学受験)#計算と数の性質#数の性質その他

指導講師：数学を数楽に

問題文全文(内容文)：
P,P+2,P+4が全て素数のとき、3つ子素数という。
3つ子素数をすべて求めよ。

投稿日：2021.06.07

＜関連動画＞

計算達人「単位変換①（長さと重さ）」小学４年生～６年生対象【毎日配信】

単元： #算数(中学受験)#文章題#単位・比と割合・比例・反比例

指導講師：中学受験算数・高校受験数学けいたくチャンネル

問題文全文(内容文)：
単位変換①（長さと重さ）に関して解説していきます。

この動画を見る　

【受験算数】30mの目盛りのついた2つの巻尺A、Bがあります。ある2地点間の距離をはかったところ、Aでは300m、Bでは420m。しかし、A、Bの巻尺を正しいものさしで比較したら8mの差がありました。

単元： #算数(中学受験)#文章題#単位・比と割合・比例・反比例

教材： #SPX#中学受験教材

指導講師：理数個別チャンネル

問題文全文(内容文)：
30mの目盛りのついた2つの巻尺A、Bがあります。ある2地点間の距離をはかったところ、Aでは300m、Bでは420mとはかれました。しかし、A、Bの巻尺を正しいものさしで比較したら8mの差がありました。次の問いに答えなさい。
(1) Aの巻尺の30mは正しいものさしで何mですか。
(2) 2地点間の距離は実際は何mですか。

この動画を見る　

こんなんできるん？

単元： #算数(中学受験)#平面図形#角度と面積#その他#算数オリンピック

指導講師：【楽しい授業動画】あきとんとん

問題文全文(内容文)：
角Cを求めよ
※図は動画内参照

この動画を見る　

マッシュの足の速さはどれくらい？

単元： #算数(中学受験)#その他#その他

指導講師：【楽しい授業動画】あきとんとん

問題文全文(内容文)：
マッシュルの主人公マッシュのビッグバンダッシュの速さに関して解説していきます。

この動画を見る　

この発想はえぐい？　大妻中

単元： #算数(中学受験)#過去問解説(学校別)#平面図形#角度と面積

指導講師：数学を数楽に

問題文全文(内容文)：
△BDFの面積=?

＊図は動画内参照

この動画を見る　

<img src="https://kaiketsu-db.net/wp-content/uploads/2021/11/112-book-morph-outline.gif" alt="" data-eio="l"> 三つ子素数

＜関連動画＞

計算達人「単位変換①（長さと重さ）」小学４年生～６年生対象【毎日配信】

【受験算数】30mの目盛りのついた2つの巻尺A、Bがあります。ある2地点間の距離をはかったところ、Aでは300m、Bでは420m。しかし、A、Bの巻尺を正しいものさしで比較したら8mの差がありました。

こんなんできるん？

マッシュの足の速さはどれくらい？

この発想はえぐい？ 大妻中

三つ子素数

この発想はえぐい？　大妻中