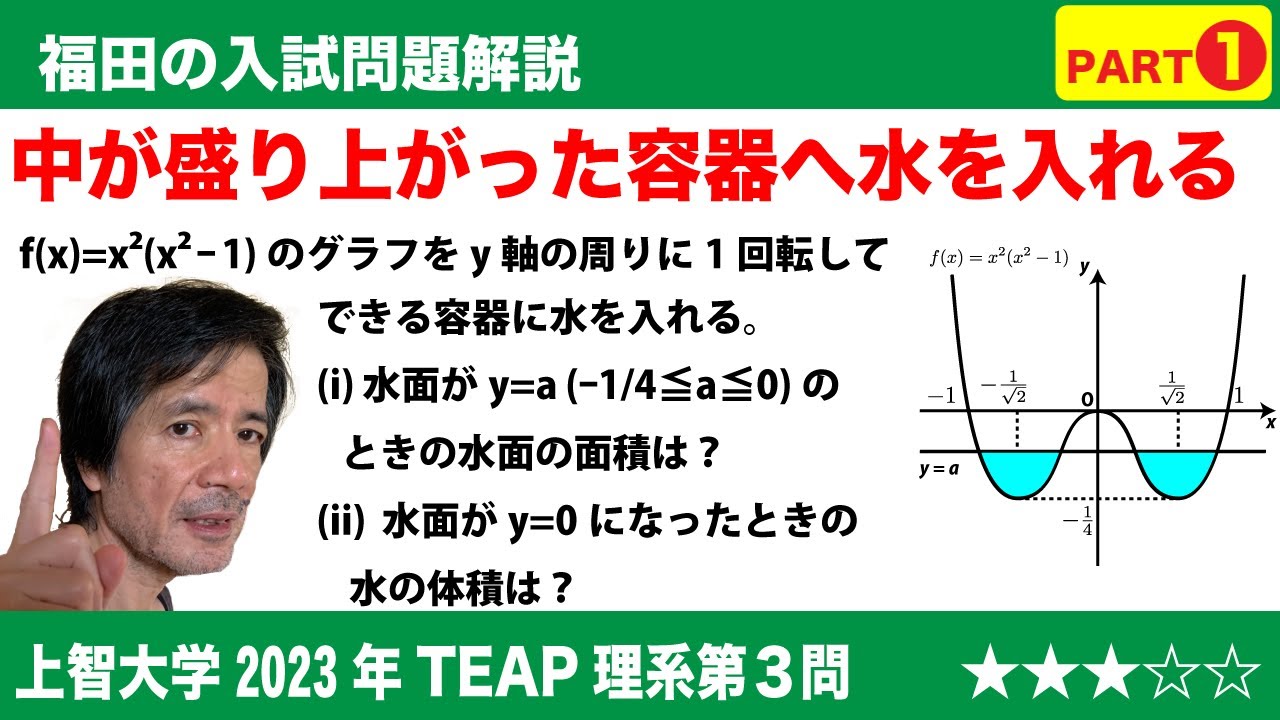
問題文全文(内容文):
$\Large\boxed{1}$
(3) 関数$y$=$\cos x\sin 2x$ $\left(0≦x≦\displaystyle\frac{\pi}{2}\right)$の最大値は$\boxed{\ \ (け)\ \ }$である。また、この関数のグラフと$x$軸で囲まれてできる図形の面積は$\boxed{\ \ (こ)\ \ }$である。
$\Large\boxed{1}$
(3) 関数$y$=$\cos x\sin 2x$ $\left(0≦x≦\displaystyle\frac{\pi}{2}\right)$の最大値は$\boxed{\ \ (け)\ \ }$である。また、この関数のグラフと$x$軸で囲まれてできる図形の面積は$\boxed{\ \ (こ)\ \ }$である。
単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{1}$
(3) 関数$y$=$\cos x\sin 2x$ $\left(0≦x≦\displaystyle\frac{\pi}{2}\right)$の最大値は$\boxed{\ \ (け)\ \ }$である。また、この関数のグラフと$x$軸で囲まれてできる図形の面積は$\boxed{\ \ (こ)\ \ }$である。
$\Large\boxed{1}$
(3) 関数$y$=$\cos x\sin 2x$ $\left(0≦x≦\displaystyle\frac{\pi}{2}\right)$の最大値は$\boxed{\ \ (け)\ \ }$である。また、この関数のグラフと$x$軸で囲まれてできる図形の面積は$\boxed{\ \ (こ)\ \ }$である。
投稿日:2024.06.23