空間上の線分の長さ 昭和学院秀英 - 質問解決D.B.（データベース）
Generic selectors
完全一致検索
タイトルから検索
記事本文から検索
Post Type Selectors
all_unit_post
質問解決D.B.（データベース） > 動画投稿 > 数学(中学生) > 中１数学 > 空間図形 > 空間上の線分の長さ　昭和学院秀英

空間上の線分の長さ　昭和学院秀英

問題文全文(内容文)：
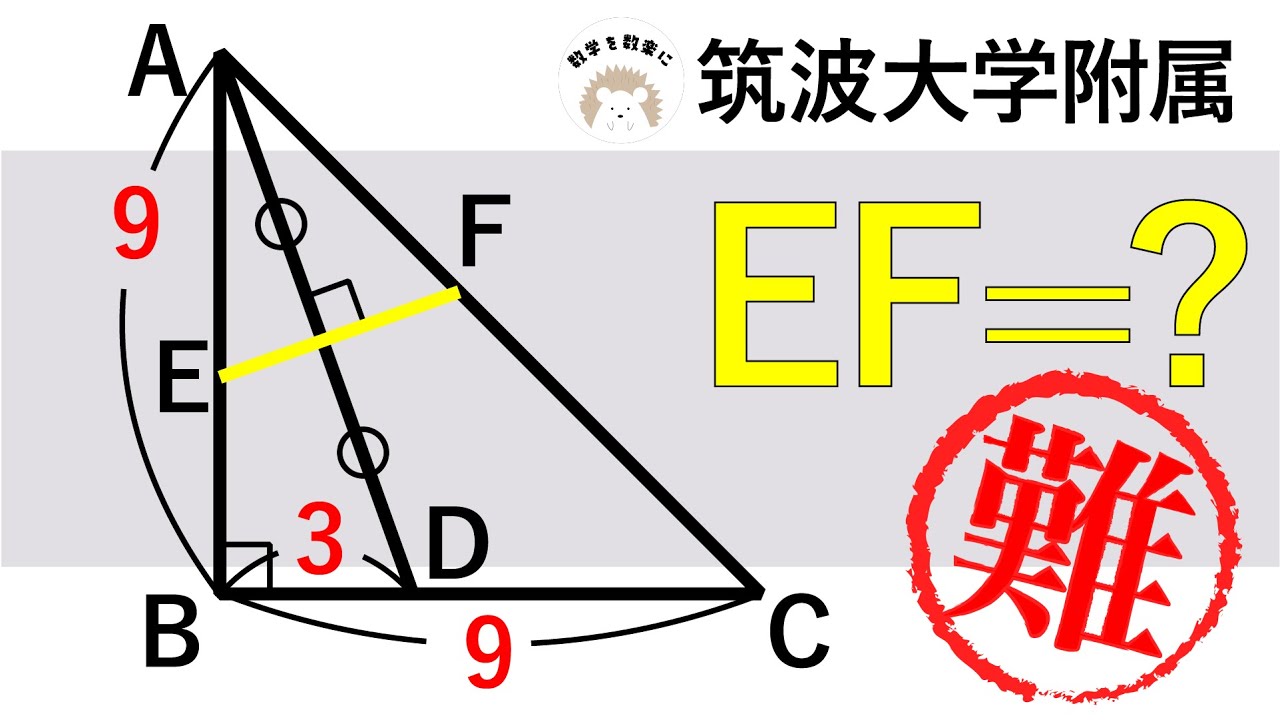
$1辺が4の立方体　平面PFHと直線CEとの交点がQ　CQ=?　（PはAEの中点）$
単元： #数学(中学生)#中１数学#空間図形
指導講師： 数学を数楽に
問題文全文(内容文)：
$1辺が4の立方体　平面PFHと直線CEとの交点がQ　CQ=?　（PはAEの中点）$
投稿日：2024.09.03

＜関連動画＞

食塩水の濃度の必勝法

アイキャッチ画像
単元： #数学(中学生)#中１数学#方程式
指導講師： 【楽しい授業動画】あきとんとん
問題文全文(内容文)：
12%の食塩水200gと7%の食塩水300gを混ぜたとき何%の食塩水か?
この動画を見る　

【数学】中2-87 箱ひげ図①(基本編)

アイキャッチ画像
単元： #数学(中学生)#中１数学#資料の活用
指導講師： とある男が授業をしてみた
問題文全文(内容文)：
数学(箱ひげ図①・基本編)

Q.
下の資料は、とある生徒9人が行った小テストの得点である。

7 5 4 9 6 7 10 3 6

①最小値は？
➁最大値は？
③第１四分位数は？
④第２四分位数は？
⑤第３四分位数は？
⑥範囲は？
⑦四分位範囲は？
⑧箱ひげ図に表しなさい。
この動画を見る　

【中学数学】動点Pの問題～比例の問題演習～ 4-1.5【中１数学】

アイキャッチ画像
単元： #数学(中学生)#中１数学#比例・反比例
指導講師： 【楽しい授業動画】あきとんとん
問題文全文(内容文)：
図のような長方形ABCDDがある点Pによっは辺AB上を秒速2cmで頂点Aから頂点Bへ動く。点Pが頂点Aを出発してから x 秒後の三角形ADPの面積を y cm²とするとき、次の問に答えよ。
（１） y を x の式で表せ。
（２） x , y の変域をそれぞれ求めよ。
（３） 三角形ADPの面積が20cm²のとき、点Pが点Aを出発してから何秒後か。
この動画を見る　

中１数学「方程式の文章題⑦（割合の問題）」【毎日配信】

アイキャッチ画像
単元： #数学(中学生)#中１数学#方程式
指導講師： 中学受験算数・高校受験数学けいたくチャンネル
問題文全文(内容文)：
中1~第31回方程式の文章題⑦~(割合の問題)

例1
何円か持って買い物に行きました。最初に所持金の3/7使い 次に残りの所持金の5/8を使ったら、90円残りました。
最初の所持金を求めなさい。(記述)

例2
ある中学校の昨年度の生徒数は360人でした。 今年度の男子は5%減り、女子は10%増えたので 全体で12人増えました。
今年度の男子を求めなさい。
この動画を見る　

受験生よ。ここで差がつきますよ。芝浦工大柏　2022入試問題解説26問目

アイキャッチ画像
単元： #数学(中学生)#中１数学#空間図形#立体図形#体積・表面積・回転体・水量・変化のグラフ#高校入試過去問(数学)
指導講師： 数学を数楽に
問題文全文(内容文)：
直方体
PF=QH=1
四角形I-MPGQの体積=?

2022芝浦工業大学柏高等学校
この動画を見る　
PAGE TOP