問題文全文(内容文):
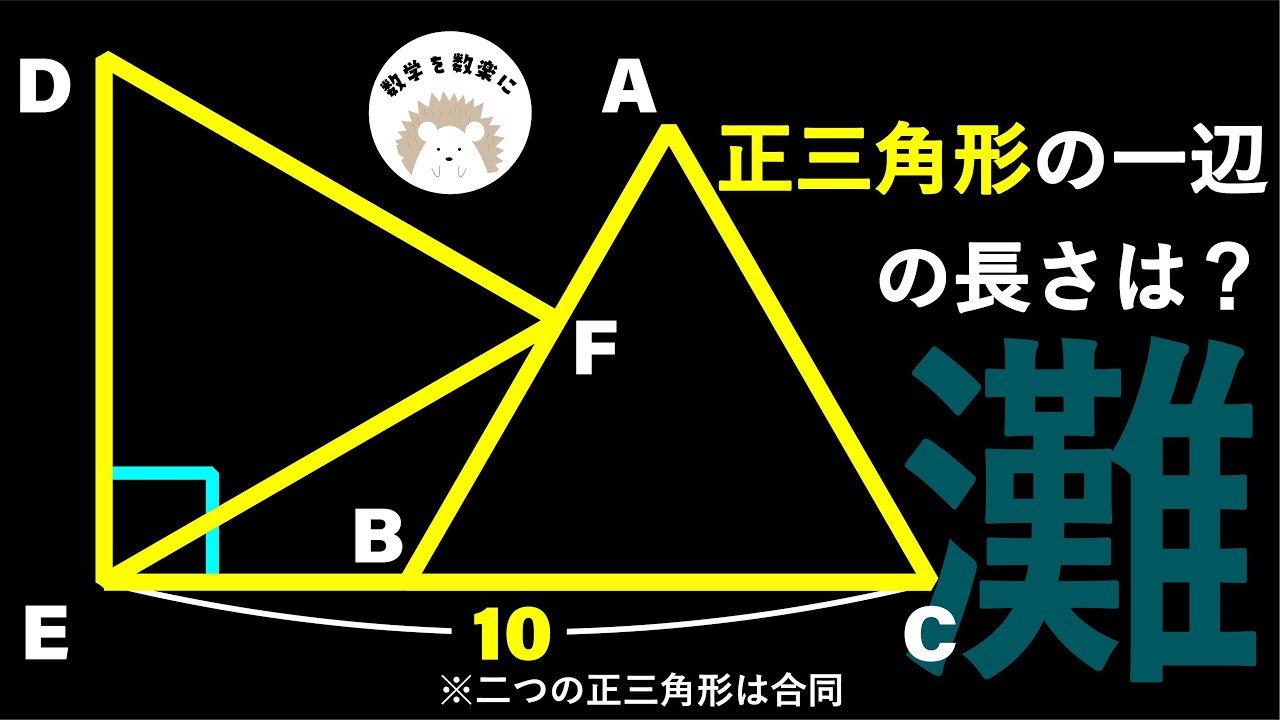
正方形の1辺の長さは?
*図は動画内参照
岡山白陵高等学校
正方形の1辺の長さは?
*図は動画内参照
岡山白陵高等学校
単元:
#数学(中学生)#中2数学#数A#図形の性質#三角形の辺の比(内分・外分・二等分線)#三角形と四角形#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
正方形の1辺の長さは?
*図は動画内参照
岡山白陵高等学校
正方形の1辺の長さは?
*図は動画内参照
岡山白陵高等学校
投稿日:2021.01.29