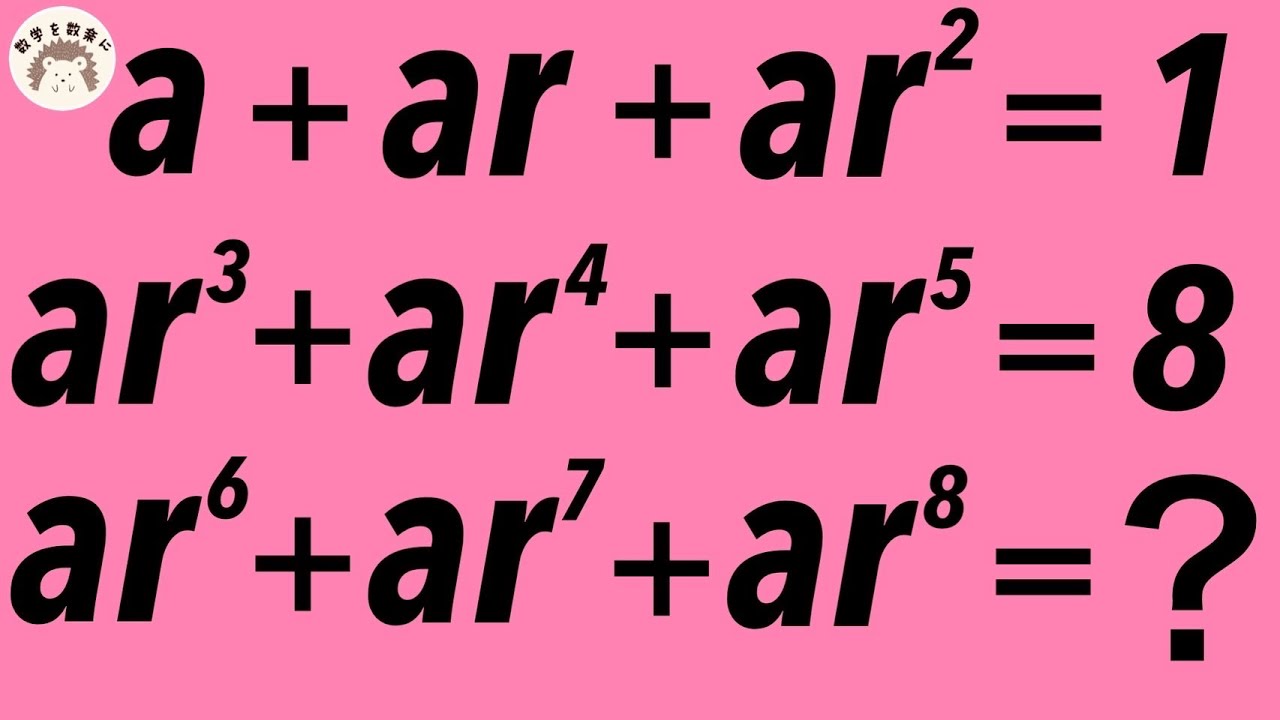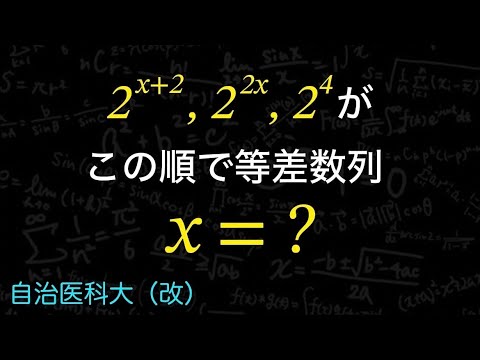問題文全文(内容文):
サイコロを$n$回振って,出た目の積を5で割った余りが1である確率$p_n$を求めよ.
サイコロを$n$回振って,出た目の積を5で割った余りが1である確率$p_n$を求めよ.
単元:
#数列#漸化式#数学(高校生)#数B
指導講師:
鈴木貫太郎
問題文全文(内容文):
サイコロを$n$回振って,出た目の積を5で割った余りが1である確率$p_n$を求めよ.
サイコロを$n$回振って,出た目の積を5で割った余りが1である確率$p_n$を求めよ.
投稿日:2020.04.30