 中学受験教材
中学受験教材
 中学受験教材
中学受験教材
【受験算数】商店Aは、ある品物を仕入れて、30%の利益を見込んで定価をつけました。商店Bは、同じ品物を商店Aより20%安く仕入れて、40%の利益を見込んで定価をつけたところ、商店Aでの定価より450…

単元:
#算数(中学受験)#文章題#単位・比と割合・比例・反比例#売買損益と食塩水
教材:
#SPX#5年算数D-支援#中学受験教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
第1問 商店Aは、ある品物を仕入れて、30%の利益を見込んで定価をつけました。商店Bは、同じ品物を商店Aより20%安く仕入れて、40%の利益を見込んで定価をつけたところ、商店Aでの定価より450円安くなりました。商店Aはいくらで仕入れましたか。
第2問 商店Aは、ある品物を仕入れて、10%の利益を見込んで定価をつけました。商店Bは、同じ品物を商店Aより10%安く仕入れて、30%の利益を見込んで定価をつけたところ、商店Aでの定価より210円高くなりました。商店Aはいくらで仕入れましたか。
この動画を見る
第1問 商店Aは、ある品物を仕入れて、30%の利益を見込んで定価をつけました。商店Bは、同じ品物を商店Aより20%安く仕入れて、40%の利益を見込んで定価をつけたところ、商店Aでの定価より450円安くなりました。商店Aはいくらで仕入れましたか。
第2問 商店Aは、ある品物を仕入れて、10%の利益を見込んで定価をつけました。商店Bは、同じ品物を商店Aより10%安く仕入れて、30%の利益を見込んで定価をつけたところ、商店Aでの定価より210円高くなりました。商店Aはいくらで仕入れましたか。
【受験算数】ある品物の定価は毎年10%ずつ値上がりし、一昨年と比べると今年は420円高くなっています。この品物の一昨年の定価はいくらですか

単元:
#算数(中学受験)#文章題#単位・比と割合・比例・反比例#売買損益と食塩水
教材:
#SPX#5年算数D-支援#中学受験教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
第1問 ある品物の定価は毎年10%ずつ値上がりし、一昨年と比べると今年は420円高くなっています。この品物の一昨年の定価はいくらですか。
第2問 ある品物の定価は毎年20%ずつ値下がりし、一昨年と比べると今年は900円安くなっています。この品物の今年の定価はいくらですか。
この動画を見る
第1問 ある品物の定価は毎年10%ずつ値上がりし、一昨年と比べると今年は420円高くなっています。この品物の一昨年の定価はいくらですか。
第2問 ある品物の定価は毎年20%ずつ値下がりし、一昨年と比べると今年は900円安くなっています。この品物の今年の定価はいくらですか。
【受験算数】原価250円のグラスを何個か仕入れました。1個360円で売ると、15個こわれて売れなかったとしても7800円の利益があります。グラスを何個仕入れましたか。

単元:
#算数(中学受験)#文章題#単位・比と割合・比例・反比例#売買損益と食塩水
教材:
#SPX#5年算数D-支援#中学受験教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
第1問 原価250円のグラスを何個か仕入れました。1個360円で売ると、15個こわれて売れなかったとしても7800円の利益があります。グラスを何個仕入れましたか。
第2問 原価300円のグラスを何個か仕入れました。1個480円で売ると、20個こわれて売れなかったとしても21900円の利益があります。グラスを何個仕入れましたか。
この動画を見る
第1問 原価250円のグラスを何個か仕入れました。1個360円で売ると、15個こわれて売れなかったとしても7800円の利益があります。グラスを何個仕入れましたか。
第2問 原価300円のグラスを何個か仕入れました。1個480円で売ると、20個こわれて売れなかったとしても21900円の利益があります。グラスを何個仕入れましたか。
【受験算数】卵を1個30円で80個仕入れましたが、そのうちの8個が割れてしまいました。残りをすべて売って、全体で2割の利益が出るようにします。全体でいくら売り上げればよいですか。

単元:
#算数(中学受験)#文章題#単位・比と割合・比例・反比例#売買損益と食塩水
教材:
#SPX#5年算数D-支援#中学受験教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
第1問 卵を1個30円で80個仕入れましたが、そのうちの8個が割れてしまいました。残りをすべて売って、全体で2割の利益が出るようにします。
(1)全体でいくら売り上げればよいですか。
(2)定価を1個いくらにすればいいですか。
第2問 卵を1個25円で600個仕入れましたが、そのうちの100個が割れてしまいました。残りをすべて売って、全体で3割の利益が出るように定価をつけると、定価を1個何円になりますか。
この動画を見る
第1問 卵を1個30円で80個仕入れましたが、そのうちの8個が割れてしまいました。残りをすべて売って、全体で2割の利益が出るようにします。
(1)全体でいくら売り上げればよいですか。
(2)定価を1個いくらにすればいいですか。
第2問 卵を1個25円で600個仕入れましたが、そのうちの100個が割れてしまいました。残りをすべて売って、全体で3割の利益が出るように定価をつけると、定価を1個何円になりますか。
【受験算数】ある品物を同じ値段でいくつか仕入れ、仕入れ値の7割の利益を見込んで1個136円の定価をつけて売りに出しましたが、5個売れ残ってしまい、売れ残った分は捨てました。その結果、 全体の利益…

単元:
#算数(中学受験)#文章題#売買損益と食塩水
教材:
#予習シ#予習シ算数・小5上#中学受験教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
ある品物を同じ値段でいくつか仕入れ、仕入れ値の7割の利益を見込んで1個136円の定価をつけて売りに出しましたが、5個売れ残ってしまい、売れ残った分は捨てました。その結果、 全体の利益は2680円になりました。品物を何個仕入れましたか。
この動画を見る
ある品物を同じ値段でいくつか仕入れ、仕入れ値の7割の利益を見込んで1個136円の定価をつけて売りに出しましたが、5個売れ残ってしまい、売れ残った分は捨てました。その結果、 全体の利益は2680円になりました。品物を何個仕入れましたか。
【受験算数】ある品物に、仕入れ値の35%の利益を見込んで定価をつけました。しかし、定価では売れなかったので定価の20%引きにしたところ、品物は売れて利益は320円になりました。この品物の仕入れ値は…

単元:
#算数(中学受験)#文章題#売買損益と食塩水
教材:
#予習シ#予習シ算数・小5上#中学受験教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の問いに答えなさい。
(1) ある品物に、仕入れ値の35%の利益を見込んで定価をつけました。しかし、定価では売れなかったので定価の20%引きにしたところ、品物は売れて利益は320円になりました。この品物の仕入れ値は何円ですか。
(2) ある品物に、仕入れ値の2割増しの定価をつけました。しかし、定価では売れなかったので定価の2割引きにしたところ、品物は売れましたが50円の損失になりました。この品物の定価は何円ですか。
この動画を見る
次の問いに答えなさい。
(1) ある品物に、仕入れ値の35%の利益を見込んで定価をつけました。しかし、定価では売れなかったので定価の20%引きにしたところ、品物は売れて利益は320円になりました。この品物の仕入れ値は何円ですか。
(2) ある品物に、仕入れ値の2割増しの定価をつけました。しかし、定価では売れなかったので定価の2割引きにしたところ、品物は売れましたが50円の損失になりました。この品物の定価は何円ですか。
【受験算数】ある品物に、仕入れ値の2割の利益を見込んで定価をつけました。しかし、定価では売れなかったので定価の1割引きにしたところ、品物は売れました。このときの利益は、定価で売れた場合よりも180円…

単元:
#算数(中学受験)#文章題#売買損益と食塩水
教材:
#予習シ#予習シ算数・小5上#中学受験教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の問いに答えなさい。
(1) ある品物に、仕入れ値の2割の利益を見込んで定価をつけました。しかし、定価では売れなかったので定価の1割引きにしたところ、品物は売れました。このときの利益は、定価で売れた場合よりも180円少なくなりました。この品物の仕入れ値は何円ですか。
(2) ある品物を仕入れ、600円の利益を見込んで定価をつけました。しかし、定価では売れなかったので定価の3割引きにしたところ、品物は売れましたが、300円の損失になりました。 この品物の仕入れ値は何円ですか。
この動画を見る
次の問いに答えなさい。
(1) ある品物に、仕入れ値の2割の利益を見込んで定価をつけました。しかし、定価では売れなかったので定価の1割引きにしたところ、品物は売れました。このときの利益は、定価で売れた場合よりも180円少なくなりました。この品物の仕入れ値は何円ですか。
(2) ある品物を仕入れ、600円の利益を見込んで定価をつけました。しかし、定価では売れなかったので定価の3割引きにしたところ、品物は売れましたが、300円の損失になりました。 この品物の仕入れ値は何円ですか。
【受験算数】あるお店では、A、B、Cの3種類の品物を売っていて、A3個、B2個、C1個の代金の合計は1770円A2個、B1個、C3個の代金の合計は2030円A1個、B3個、C2個の代金の合計は…

単元:
#算数(中学受験)#文章題#文章題その他
教材:
#予習シ#予習シリーズ算数・小6下(難関校編)#中学受験教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
あるお店では、A、B、Cの3種類の品物を売っていて、
A3個、B2個、C1個の代金の合計は1770円
A2個、B1個、C3個の代金の合計は2030円
A1個、B3個、C2個の代金の合計は2020円
です。これについて、次の問いに答えなさい。
(1)A1個、B1個、C1個の代金の合計は何円ですか。
(2)A2個、B3個、C1個の代金の合計は何円ですか。
この動画を見る
あるお店では、A、B、Cの3種類の品物を売っていて、
A3個、B2個、C1個の代金の合計は1770円
A2個、B1個、C3個の代金の合計は2030円
A1個、B3個、C2個の代金の合計は2020円
です。これについて、次の問いに答えなさい。
(1)A1個、B1個、C1個の代金の合計は何円ですか。
(2)A2個、B3個、C1個の代金の合計は何円ですか。
【受験算数】太郎君、次郎君、三郎君の3人が遊園地に行きました。太郎君はバス代、次郎君は入園料、三郎君は昼食代をそれぞれ3人分ずつ払いました。このとき、次郎君が払った金額は、太郎君が払った金額の2倍と…

単元:
#算数(中学受験)#文章題#文章題その他
教材:
#予習シ#予習シリーズ算数・小6下(難関校編)#中学受験教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
太郎君、次郎君、三郎君の3人が遊園地に行きました。太郎君はバス代、次郎君は入園料、三郎君は昼食代をそれぞれ3人分ずつ払いました。このとき、次郎君が払った金額は、太郎君が払った金額の2倍と三郎君が払った金額の合計と同じでした。翌日、3人は1人分の費用が同じになるように計算して、太郎君は次郎君に1100円、三郎君は次郎君に350円払いました。これについて、次の問いに答えなさい。
(1)1人分のバス代は何円ですか。
(2)1人分の入園料、昼食代はそれぞれ何円ですか。
この動画を見る
太郎君、次郎君、三郎君の3人が遊園地に行きました。太郎君はバス代、次郎君は入園料、三郎君は昼食代をそれぞれ3人分ずつ払いました。このとき、次郎君が払った金額は、太郎君が払った金額の2倍と三郎君が払った金額の合計と同じでした。翌日、3人は1人分の費用が同じになるように計算して、太郎君は次郎君に1100円、三郎君は次郎君に350円払いました。これについて、次の問いに答えなさい。
(1)1人分のバス代は何円ですか。
(2)1人分の入園料、昼食代はそれぞれ何円ですか。
【受験算数】(図1)のような直方体の形の容器があります。容器の底は、側面と平行な長方形の仕切り板でA. B. Cの3つの部分に分けられています。(図2)のグラフは、容器が空の状態から、Aの部分に一定…
単元:
#算数(中学受験)#立体図形#体積・表面積・回転体・水量・変化のグラフ
教材:
#予習シ#予習シ算数・小5上#中学受験教材#立体図形
指導講師:
理数個別チャンネル
問題文全文(内容文):
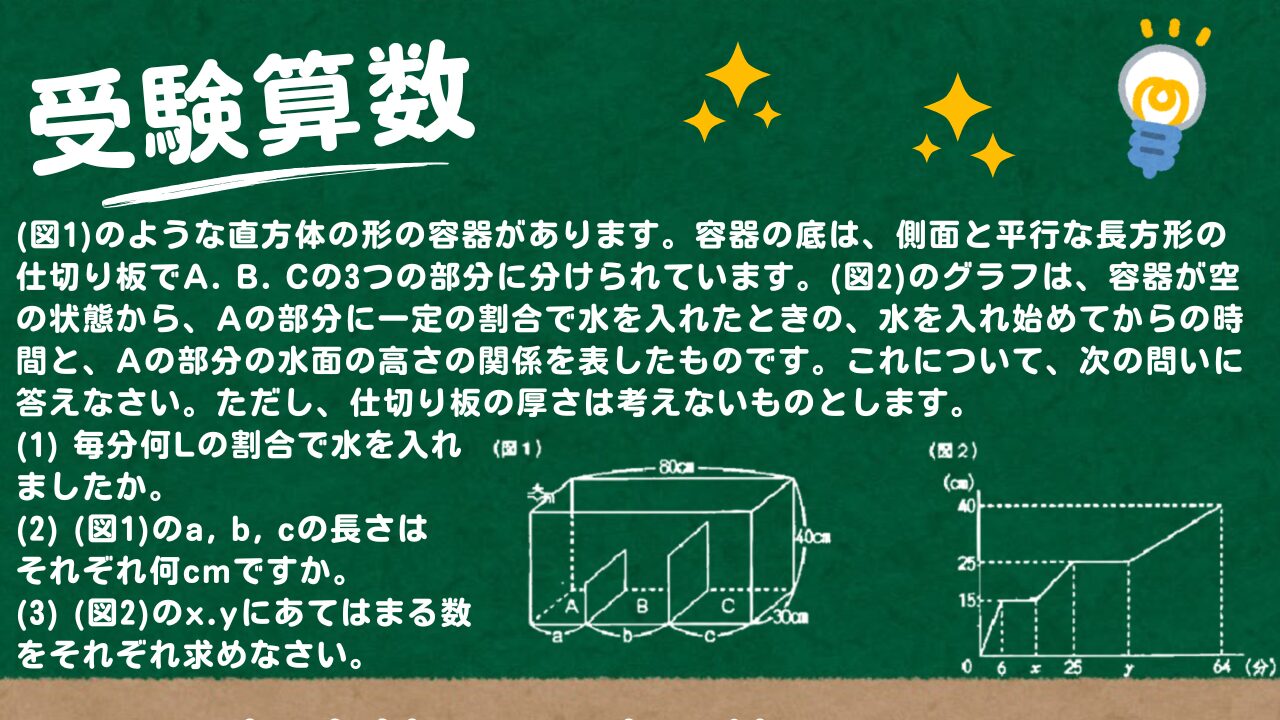
(図1)のような直方体の形の容器があります。容器の底は、側面と平行な長方形の仕切り板でA. B. Cの3つの部分に分けられています。(図2)のグラフは、容器が空の状態から、Aの部分に一定の割合で水を入れたときの、水を入れ始めてからの時間と、Aの部分の水面の高さの関係を表したものです。これについて、次の問いに答えなさい。ただし、仕切り板の厚さは考えないものとします。
(1) 毎分何Lの割合で水を入れましたか。
(2) (図1)のa, b, cの長さはそれぞれ何cmですか。
(3) (図2)のx.yにあてはまる数をそれぞれ求めなさい。
この動画を見る
(図1)のような直方体の形の容器があります。容器の底は、側面と平行な長方形の仕切り板でA. B. Cの3つの部分に分けられています。(図2)のグラフは、容器が空の状態から、Aの部分に一定の割合で水を入れたときの、水を入れ始めてからの時間と、Aの部分の水面の高さの関係を表したものです。これについて、次の問いに答えなさい。ただし、仕切り板の厚さは考えないものとします。
(1) 毎分何Lの割合で水を入れましたか。
(2) (図1)のa, b, cの長さはそれぞれ何cmですか。
(3) (図2)のx.yにあてはまる数をそれぞれ求めなさい。
【受験算数】(図1)のように、円柱の形の容器の底に円柱のおもりBが置かれています。この容器に毎分6Lの割合で水を入れました。(図2)のグラフは、水を入れ始めてからの時間と水面の高さの関係を表した…

単元:
#算数(中学受験)#立体図形#体積・表面積・回転体・水量・変化のグラフ
教材:
#予習シ#予習シ算数・小5上#中学受験教材#立体図形
指導講師:
理数個別チャンネル
問題文全文(内容文):
(図1)のように、円柱の形の容器の底に円柱のおもりBが置かれています。この容器に毎分6Lの割合で水を入れました。(図2)のグラフは、水を入れ始めてからの時間と水面の高さの関係を表したものです。 これについて、次の問いに答えなさい。
(1) 容器の底面積は何cmですか。
(2) おもりBの底面積は何cmですか。
(3) おもりBの高さは何cmですか。
この動画を見る
(図1)のように、円柱の形の容器の底に円柱のおもりBが置かれています。この容器に毎分6Lの割合で水を入れました。(図2)のグラフは、水を入れ始めてからの時間と水面の高さの関係を表したものです。 これについて、次の問いに答えなさい。
(1) 容器の底面積は何cmですか。
(2) おもりBの底面積は何cmですか。
(3) おもりBの高さは何cmですか。
【中学受験理科】てこの応用③:長さが72cmで、太さが一様な重さ300gの針金を用いて、次の図1~図4のようにしました。曲げた部分の長さを考えないとすると、①~④は何cmですか。

単元:
#理科(中学受験)#物理分野
教材:
#マスターテキスト#マスターテキスト理科演習編standard#中学受験教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
長さが72cmで、太さが一様な重さ300gの針金を用いて、次の図1~図4のようにしました。
曲げた部分の長さを考えないとすると、①~④は何cmですか。
この動画を見る
長さが72cmで、太さが一様な重さ300gの針金を用いて、次の図1~図4のようにしました。
曲げた部分の長さを考えないとすると、①~④は何cmですか。
【中学受験理科】てこの応用②:図1のような重さ100gの棒を何本か使ってはり合わせ、棒をつり合わせました。これについて、 次の問いに答えなさい。問1 図2、図3のように2本の棒をつり合わせたとき、

単元:
#理科(中学受験)#物理分野
教材:
#マスターテキスト#マスターテキスト理科演習編standard#中学受験教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
図1のような重さ100gの棒を何本か使ってはり合わせ、棒をつり合わせました。これについて、 次の問いに答えなさい。
問1 図2、図3のように2本の棒をつり合わせたとき、①の長さと②~④のばねはかりの示す値を 答えなさい。
問2 図4、図5のように2本の棒をつり合わせたとき、⑤の長さと⑥~⑧のばねはかりの示す値を 答えなさい。
この動画を見る
図1のような重さ100gの棒を何本か使ってはり合わせ、棒をつり合わせました。これについて、 次の問いに答えなさい。
問1 図2、図3のように2本の棒をつり合わせたとき、①の長さと②~④のばねはかりの示す値を 答えなさい。
問2 図4、図5のように2本の棒をつり合わせたとき、⑤の長さと⑥~⑧のばねはかりの示す値を 答えなさい。
【中学受験理科】てこの応用①:問1 支点のところで糸につながれたア〜ウの金あみに、いろいろな重さのおもりがつるされています。金あみを水平につり合わせるためには、20gのおもりをどこにつるせばよいか

単元:
#理科(中学受験)#物理分野
教材:
#マスターテキスト#マスターテキスト理科演習編standard#中学受験教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
問1 支点のところで糸につながれたア〜ウの金あみに、いろいろな重さのおもりがつるされていま す。金あみを水平につり合わせるためには、20gのおもりをどこにつるせばよいか、それぞれ答えなさい。なお、一番左上につける場合は (1.A) のように答えなさい。
材質と厚さが一様な三角形の板を、図1のようにばねはかりでつるすと、それぞれ60g. 120 g. 90gを示して水平になりました。これについて、次の問いに答えなさい。
問2 図2のように、線AB上のD点をつるして、水平につり合わせました。このとき、D点はA点 から何cmのところにありますか。
問3 図3のように、線CD上のG点をつるして、水平につり合わせました。CDの長さが24cm のとき、G点はC点から何cmのところにありますか。また、ばねはかりは何gを示しますか。
この動画を見る
問1 支点のところで糸につながれたア〜ウの金あみに、いろいろな重さのおもりがつるされていま す。金あみを水平につり合わせるためには、20gのおもりをどこにつるせばよいか、それぞれ答えなさい。なお、一番左上につける場合は (1.A) のように答えなさい。
材質と厚さが一様な三角形の板を、図1のようにばねはかりでつるすと、それぞれ60g. 120 g. 90gを示して水平になりました。これについて、次の問いに答えなさい。
問2 図2のように、線AB上のD点をつるして、水平につり合わせました。このとき、D点はA点 から何cmのところにありますか。
問3 図3のように、線CD上のG点をつるして、水平につり合わせました。CDの長さが24cm のとき、G点はC点から何cmのところにありますか。また、ばねはかりは何gを示しますか。
【受験算数】(図1)のような直方体の形の容器に3Lの水を入れたところ、水の深さは8cmになりました。この容器を、辺DEを床につけたまま、静かにかたむけていきました。(図2)は、水面が辺ADの真ん中の…
単元:
#算数(中学受験)#立体図形#体積・表面積・回転体・水量・変化のグラフ
教材:
#予習シ#予習シ算数・小5上#中学受験教材#立体図形
指導講師:
理数個別チャンネル
問題文全文(内容文):
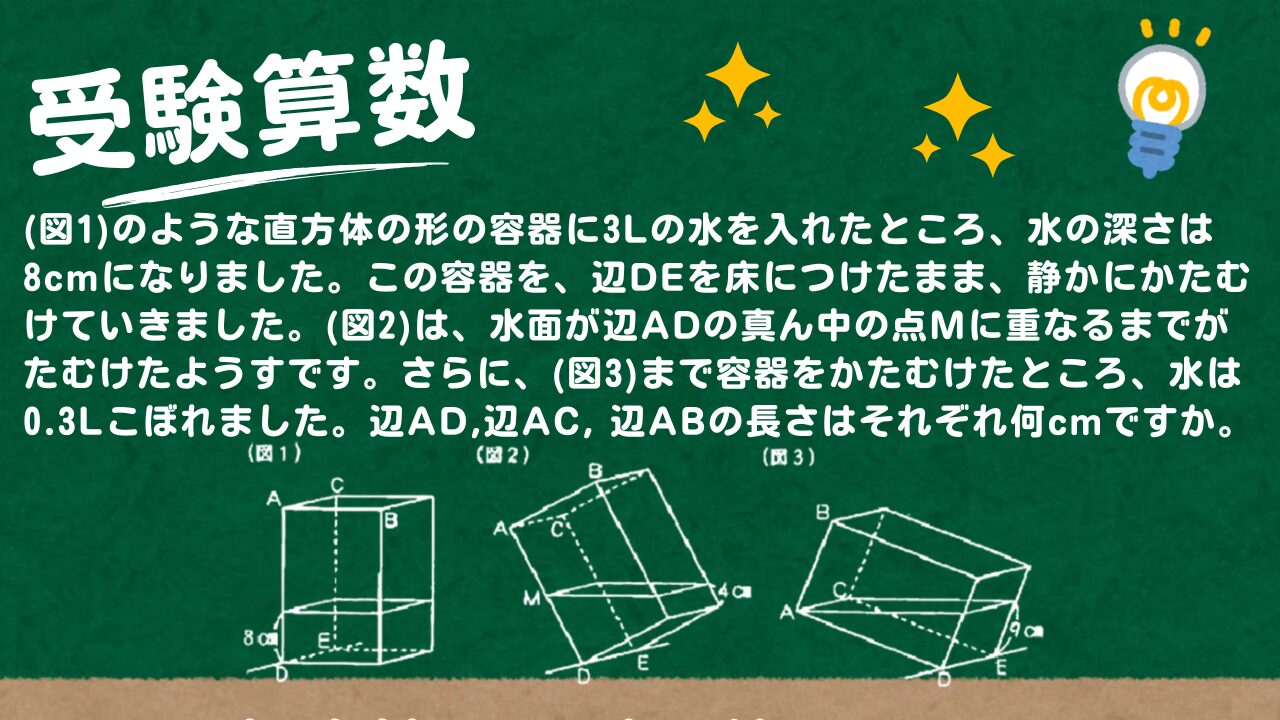
(図1)のような直方体の形の容器に3Lの水を入れたところ、水の深さは8cmになりました。この容器を、辺DEを床につけたまま、静かにかたむけていきました。(図2)は、水面が辺ADの真ん中の点Mに重なるまでがたむけたようすです。さらに、(図3)まで容器をかたむけたところ、水は0.3Lこぼれました。辺AD,辺AC, 辺ABの長さはそれぞれ何cmですか。
この動画を見る
(図1)のような直方体の形の容器に3Lの水を入れたところ、水の深さは8cmになりました。この容器を、辺DEを床につけたまま、静かにかたむけていきました。(図2)は、水面が辺ADの真ん中の点Mに重なるまでがたむけたようすです。さらに、(図3)まで容器をかたむけたところ、水は0.3Lこぼれました。辺AD,辺AC, 辺ABの長さはそれぞれ何cmですか。
【受験算数】(図1)のような、直方体を組み合わせた形の容器が床に固定されています。この容器に毎分0.6Lの割合で水を入れました。(図2)のグラフは、水を入れ始めてからの時間と水面の高さの関係を表した…
単元:
#算数(中学受験)#立体図形#体積・表面積・回転体・水量・変化のグラフ
教材:
#予習シ#予習シ算数・小5上#中学受験教材#立体図形
指導講師:
理数個別チャンネル
問題文全文(内容文):
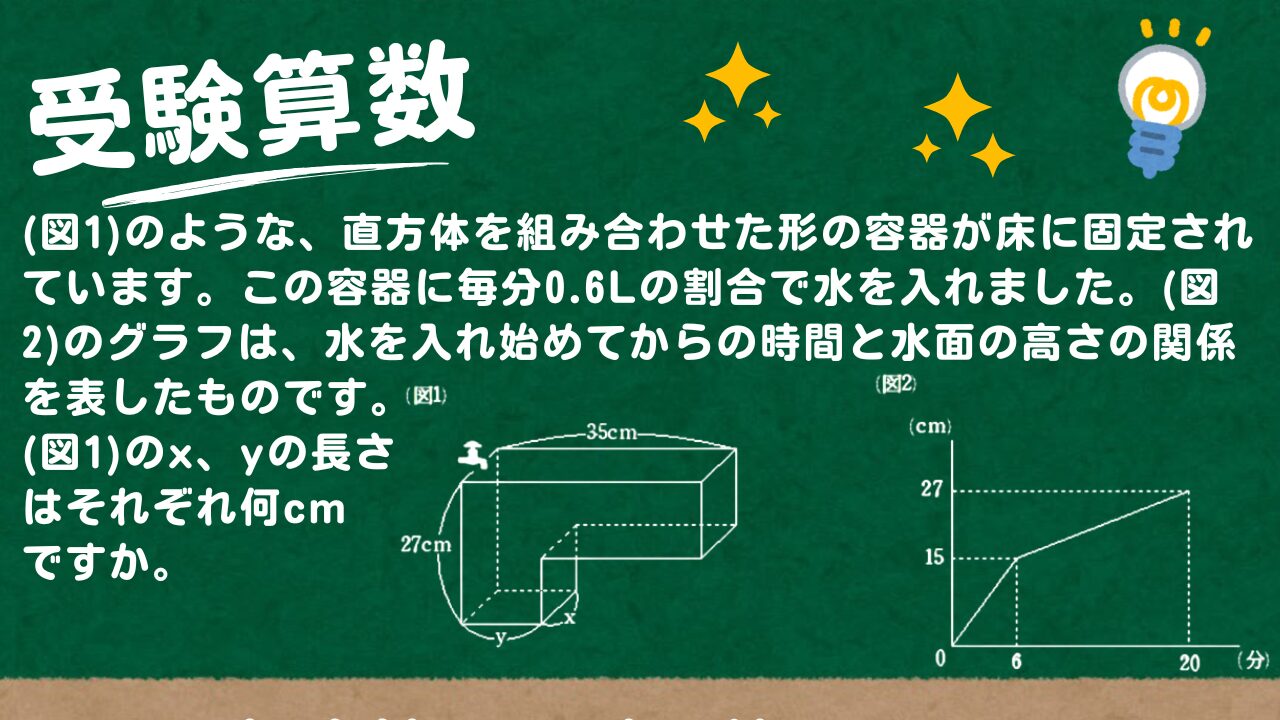
(図1)のような、直方体を組み合わせた形の容器が床に固定されています。この容器に毎分0.6Lの割合で水を入れました。(図2)のグラフは、水を入れ始めてからの時間と水面の高さの関係を表したものです。(図1)のx、yの長さはそれぞれ何cmですか。
この動画を見る
(図1)のような、直方体を組み合わせた形の容器が床に固定されています。この容器に毎分0.6Lの割合で水を入れました。(図2)のグラフは、水を入れ始めてからの時間と水面の高さの関係を表したものです。(図1)のx、yの長さはそれぞれ何cmですか。
【中学受験理科】てこ基礎4:太さが一様でない棒の端にばねばかりをつけて重さをはかると、図のようになりました。問1下の①・➁にあてはまる数字を答えなさい。問2下の③~⑤にあてはまる数字を答えなさい。

単元:
#理科(中学受験)#物理分野
教材:
#マスターテキスト#マスターテキスト理科演習編standard#中学受験教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
太さが一様でない棒の端にばねばかりをつけて重さをはかると、図のようになりました。
問1下の①・➁にあてはまる数字を答えなさい。
問2下の③~⑤にあてはまる数字を答えなさい。
この動画を見る
太さが一様でない棒の端にばねばかりをつけて重さをはかると、図のようになりました。
問1下の①・➁にあてはまる数字を答えなさい。
問2下の③~⑤にあてはまる数字を答えなさい。
【中学受験理科】てこ基礎3:120gの棒とおもりを使って、下の図のようにつり合わせました。問1下の①・②にあてはまる数字を答えなさい。問2下の③~⑧にあてはまる数字を答えなさい。

単元:
#理科(中学受験)#物理分野
教材:
#マスターテキスト#マスターテキスト理科演習編standard#中学受験教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
120gの棒とおもりを使って、下の図のようにつり合わせました。
問1下の①・②にあてはまる数字を答えなさい。
問2下の③~⑧にあてはまる数字を答えなさい。
この動画を見る
120gの棒とおもりを使って、下の図のようにつり合わせました。
問1下の①・②にあてはまる数字を答えなさい。
問2下の③~⑧にあてはまる数字を答えなさい。
【受験算数】パーティー会場に丸テーブルが大小合わせて17個あります。大きいテーブルに7人ずつ、小さいテーブルに5人ずつ座ると2人座れないので、大きいテーブルには 8人ずつ、小さいテーブルには4人ずつ…

単元:
#算数(中学受験)#文章題#和差算・植木算・分配算・倍数算・年齢算・相当算・つるかめ算#平均算・過不足算・差集め算・消去算
教材:
#SPX#5年算数D-支援#中学受験教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
パーティー会場に丸テーブルが大小合わせて17個あります。大きいテーブルに7人ずつ、小さいテーブルに5人ずつ座ると2人座れないので、大きいテーブルには 8人ずつ、小さいテーブルには4人ずつ座ることにしたら1人分の席が余ります。 大きいテーブルは何個ありますか。また、パーティーに集まった人は何人ですか。
この動画を見る
パーティー会場に丸テーブルが大小合わせて17個あります。大きいテーブルに7人ずつ、小さいテーブルに5人ずつ座ると2人座れないので、大きいテーブルには 8人ずつ、小さいテーブルには4人ずつ座ることにしたら1人分の席が余ります。 大きいテーブルは何個ありますか。また、パーティーに集まった人は何人ですか。
【受験算数】あるクラスの生徒36人に鉛筆を配ることにしました。男子に5本ずつ、女子に4本ずつ配ると56本余ることがわかりました。そこで、新たに12本を追加して男子に 6本ずつ、女子に7本ずつ配ると…

単元:
#算数(中学受験)#文章題#和差算・植木算・分配算・倍数算・年齢算・相当算・つるかめ算#平均算・過不足算・差集め算・消去算
教材:
#SPX#5年算数D-支援#中学受験教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
あるクラスの生徒36人に鉛筆を配ることにしました。男子に5本ずつ、女子に4本ずつ配ると56本余ることがわかりました。そこで、新たに12本を追加して男子に 6本ずつ、女子に7本ずつ配ると過不足はありませんでした。はじめに用意していた鉛筆は何本ですか。
この動画を見る
あるクラスの生徒36人に鉛筆を配ることにしました。男子に5本ずつ、女子に4本ずつ配ると56本余ることがわかりました。そこで、新たに12本を追加して男子に 6本ずつ、女子に7本ずつ配ると過不足はありませんでした。はじめに用意していた鉛筆は何本ですか。
【中学受験理科】図のような装置を使い。レールの斜面上で金属球を転がして木片と衝突させ、木片が動いた距離をはかりました。使った金属球の重さ・レールの高さと木片が動いた距離をまとめると、表1・表2のように

単元:
#理科(中学受験)#物理分野
教材:
#マスターテキスト#マスターテキスト理科演習編standard#中学受験教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
図のような装置を使い。レールの斜面上で金属球を転がして木片と衝突させ、木片が動いた距離をはかりました。使った金属球の重さ・レールの高さと木片が動いた距離をまとめると、表1・表2のようになりました。これについて、次の問いに答えなさい。
問1 表の①・②にあてはまる距離は何cmですか。それぞれ数字で答えなさい
問2 レールの高さを25cmにして、200gの金属球を転がすと、木片が動く距離は何cmになり
ますか。数字で答えなさい。
問3 レールの高さを150mにして、120gの金属球を転がすと、木片が動く距離は何cmになり
ますか。数字で答えなさい。
この動画を見る
図のような装置を使い。レールの斜面上で金属球を転がして木片と衝突させ、木片が動いた距離をはかりました。使った金属球の重さ・レールの高さと木片が動いた距離をまとめると、表1・表2のようになりました。これについて、次の問いに答えなさい。
問1 表の①・②にあてはまる距離は何cmですか。それぞれ数字で答えなさい
問2 レールの高さを25cmにして、200gの金属球を転がすと、木片が動く距離は何cmになり
ますか。数字で答えなさい。
問3 レールの高さを150mにして、120gの金属球を転がすと、木片が動く距離は何cmになり
ますか。数字で答えなさい。
【中学受験理科】図1のように摩擦のない斜面上の点Aから球を転がし、O.1秒ごとに進んだ距離を調べました。問1 AからDに進んだときの平均の速さは何cm/秒ですか。問2 球の重さを2倍にすると、Aから

単元:
#理科(中学受験)#物理分野
教材:
#マスターテキスト#マスターテキスト理科演習編standard#中学受験教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
図1のように摩擦のない斜面上の点Aから球を転がし、O.1秒ごとに進んだ距離を調べました。
問1 AからDに進んだときの平均の速さは何cm/秒ですか。
問2 球の重さを2倍にすると、AからDに進んだときの平均の速さは何cm/秒になりますか。
次に、図1のある点から球を転がし、DE間を0.1秒ごとに進んだ距離を調べたところ、図2のようになりました。
問3 DE間の球の速さは何cm/秒ですか。
この動画を見る
図1のように摩擦のない斜面上の点Aから球を転がし、O.1秒ごとに進んだ距離を調べました。
問1 AからDに進んだときの平均の速さは何cm/秒ですか。
問2 球の重さを2倍にすると、AからDに進んだときの平均の速さは何cm/秒になりますか。
次に、図1のある点から球を転がし、DE間を0.1秒ごとに進んだ距離を調べたところ、図2のようになりました。
問3 DE間の球の速さは何cm/秒ですか。
【受験算数】あるお店では、クリスマスケーキいくつかをまとめて仕入れました。もしも、すべてのケーキを1個3000円で売ると、50000円の利益が出ます。実際は、仕入れたケーキのうち、何個かを…

単元:
#算数(中学受験)#文章題#和差算・植木算・分配算・倍数算・年齢算・相当算・つるかめ算#平均算・過不足算・差集め算・消去算
教材:
#SPX#5年算数D-支援#中学受験教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
あるお店では、クリスマスケーキいくつかをまとめて仕入れました。
もしも、すべてのケーキを1個3000円で売ると、50000円の利益が出ます。
実際は、仕入れたケーキのうち、何個かを1個2800円で売り、残りのケーキを1個2500円で10個売ったところ、7個売れ残ってしまい廃棄しましたが、10000円の利益が出ました。
仕入れたケーキは何個ですか。
この動画を見る
あるお店では、クリスマスケーキいくつかをまとめて仕入れました。
もしも、すべてのケーキを1個3000円で売ると、50000円の利益が出ます。
実際は、仕入れたケーキのうち、何個かを1個2800円で売り、残りのケーキを1個2500円で10個売ったところ、7個売れ残ってしまい廃棄しましたが、10000円の利益が出ました。
仕入れたケーキは何個ですか。
【中学受験理科】鏡に次のように光を当てました。問1 図1で、反射角は何度ですか。問2 図1の鏡を、A点を中心に時計まわりに 15°回転させて図2のようにすると、角度aは何度になりますか。

単元:
#理科(中学受験)#物理分野
教材:
#マスターテキスト#マスターテキスト理科演習編standard#中学受験教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
鏡に次のように光を当てました。
問1 図1で、反射角は何度ですか。
問2 図1の鏡を、A点を中心に時計まわりに 15°回転させて図2のようにすると、角度aは何度
になりますか。
問3 図1の鏡を、A点を中心に反時計まわりに回転させると、反射角が40°になりました。回転
させた角度は何度ですか。
この動画を見る
鏡に次のように光を当てました。
問1 図1で、反射角は何度ですか。
問2 図1の鏡を、A点を中心に時計まわりに 15°回転させて図2のようにすると、角度aは何度
になりますか。
問3 図1の鏡を、A点を中心に反時計まわりに回転させると、反射角が40°になりました。回転
させた角度は何度ですか。
【中学受験理科】次の図のように点光源を置いたところ、Xの長さによってYの長さが変化しました。問1 Xの長さが20cmのとき、Yの長さが20cmになりました。レンズの焦点距離は何cmですか。

単元:
#理科(中学受験)#物理分野
教材:
#マスターテキスト#マスターテキスト理科演習編standard#中学受験教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の図のように点光源を置いたところ、Xの長さによってYの長さが変化しました。
問1 Xの長さが20cmのとき、Yの長さが20cmになりました。レンズの焦点距離は何cmですか。
問2 Xの長さが12cmのとき、レンズを通った光はどうなりますか。次のア~エから選びなさい。
ア レンズを通った光がレンズの反対側に集まり、Yの長さは20cmより短くなる。
イ レンズを通った光がレンズの反対側に集まり、Yの長さは20cmより長くなる。
ウ レンズを通った光が平行光線となる。
エ レンズを通った光が拡散光線となる。
問3 Xの長さが10cmのとき、レンズを通った光はどうなりますか。問2のア~エから選びなさい。
この動画を見る
次の図のように点光源を置いたところ、Xの長さによってYの長さが変化しました。
問1 Xの長さが20cmのとき、Yの長さが20cmになりました。レンズの焦点距離は何cmですか。
問2 Xの長さが12cmのとき、レンズを通った光はどうなりますか。次のア~エから選びなさい。
ア レンズを通った光がレンズの反対側に集まり、Yの長さは20cmより短くなる。
イ レンズを通った光がレンズの反対側に集まり、Yの長さは20cmより長くなる。
ウ レンズを通った光が平行光線となる。
エ レンズを通った光が拡散光線となる。
問3 Xの長さが10cmのとき、レンズを通った光はどうなりますか。問2のア~エから選びなさい。
【中学受験理科】次の図のように4cmの物体を置いたところ、4cmの像ができました。問1 レンズの焦点距離は何cmですか。問2レンズから 10cmのところに物体を置くと、上の図と比べて像はどうなりますか

単元:
#理科(中学受験)#物理分野
教材:
#マスターテキスト#マスターテキスト理科演習編standard#中学受験教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の図のように4cmの物体を置いたところ、4cmの像ができました。
問1 レンズの焦点距離は何cmですか。
問2レンズから 10cmのところに物体を置くと、上の図と比べて像はどうなりますか。次のア~力から選びなさい。
ア像の位置はレンズに近づき、像は大きくなる。
イ像の位置はレンズに近づき、像は小さくなる。
ウ像の位置はレンズから遠ざかり、像は大きくなる。
工像の位置はレンズから遠ざかり、像は小さくなる。
オ像はできない。
力物体の反対側からレンズをのぞくと、大きな正立虚像が見える。
問3
レンズから4cmのところに物体を置くと像はどうなりますか。問2のア~力から選びなさい。
この動画を見る
次の図のように4cmの物体を置いたところ、4cmの像ができました。
問1 レンズの焦点距離は何cmですか。
問2レンズから 10cmのところに物体を置くと、上の図と比べて像はどうなりますか。次のア~力から選びなさい。
ア像の位置はレンズに近づき、像は大きくなる。
イ像の位置はレンズに近づき、像は小さくなる。
ウ像の位置はレンズから遠ざかり、像は大きくなる。
工像の位置はレンズから遠ざかり、像は小さくなる。
オ像はできない。
力物体の反対側からレンズをのぞくと、大きな正立虚像が見える。
問3
レンズから4cmのところに物体を置くと像はどうなりますか。問2のア~力から選びなさい。
【受験算数】あるお店では、卵いくつかをまとめて仕入れました。もしも、すべての卵を1個 25円で売ると、300円の利益が出ます。実際は、仕入れた卵のうち、10個をタイムセールで1個15円で売り、残りの…

単元:
#算数(中学受験)#文章題#和差算・植木算・分配算・倍数算・年齢算・相当算・つるかめ算#平均算・過不足算・差集め算・消去算
教材:
#SPX#5年算数D-支援#中学受験教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
あるお店では、卵いくつかをまとめて仕入れました。
もしも、すべての卵を1個 25円で売ると、300円の利益が出ます。
実際は、仕入れた卵のうち、10個をタイムセールで1個15円で売り、
残りの卵を1個30円で売ったところ、3個売れ残り廃棄しましたが、400円の利益が出ました。
仕入れた卵は何個ですか。
この動画を見る
あるお店では、卵いくつかをまとめて仕入れました。
もしも、すべての卵を1個 25円で売ると、300円の利益が出ます。
実際は、仕入れた卵のうち、10個をタイムセールで1個15円で売り、
残りの卵を1個30円で売ったところ、3個売れ残り廃棄しましたが、400円の利益が出ました。
仕入れた卵は何個ですか。
【受験算数】折り紙を2人には10枚ずつ、3人には9枚ずつ配り、残りの人には5枚ずつ配ったら、19枚残りました。そこで、改めて全員に6枚ずつ配ろうとしたら、4枚足りませんでした。折り紙の枚数と…

単元:
#算数(中学受験)#文章題#和差算・植木算・分配算・倍数算・年齢算・相当算・つるかめ算#平均算・過不足算・差集め算・消去算
教材:
#SPX#5年算数D-支援#中学受験教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
折り紙を2人には10枚ずつ、3人には9枚ずつ配り、残りの人には5枚ずつ配ったら、19枚残りました。
そこで、改めて全員に6枚ずつ配ろうとしたら、4枚足りませんでした。
折り紙の枚数と人数を求めなさい。
この動画を見る
折り紙を2人には10枚ずつ、3人には9枚ずつ配り、残りの人には5枚ずつ配ったら、19枚残りました。
そこで、改めて全員に6枚ずつ配ろうとしたら、4枚足りませんでした。
折り紙の枚数と人数を求めなさい。
【中学受験理科】図1のような装置を使って、0.1g、0.2g、0.3gの二酸化マンガンに、それぞれ20㎤の過酸化水素水を加え、発生する酸素をすべてメスシリンダーに集めました。発生した酸素の体積と時間の

単元:
#理科(中学受験)#化学分野
教材:
#マスターテキスト#マスターテキスト理科演習編standard#中学受験教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
図1のような装置を使って、0.1g、0.2g、0.3gの二酸化マンガンに、それぞれ20㎤の過酸化水素水を加え、発生する酸素をすべてメスシリンダーに集めました。発生した酸素の体積と時間の関係をグラフに表すと図2のようになりました
問1 図2の(あ)~(う)のグラフで、0.3gの二酸化マンガンを使ったときを結果を表しているものはどれですか
問2 同じ濃さの過酸化水素35㎤に、0.3gの二酸化マンガンを加えて実験を行うと、発生する酸素の体積は何㎤になりますか
問3 2倍の濃さの過酸化水素15㎤に、0.8gの二酸化マンガンを加えて実験を行うと、発生する酸素の体積は何㎤になりますか
問4 ある濃さの過酸化水素12.5㎤に0.1gの二酸化マンガンを加えて実験を行うと、発生する酸素の体積は90㎤になりました。この過酸化水素の濃さはグラフのときの過酸化水素の濃さの何倍ですか
※表や図は動画内に記載
この動画を見る
図1のような装置を使って、0.1g、0.2g、0.3gの二酸化マンガンに、それぞれ20㎤の過酸化水素水を加え、発生する酸素をすべてメスシリンダーに集めました。発生した酸素の体積と時間の関係をグラフに表すと図2のようになりました
問1 図2の(あ)~(う)のグラフで、0.3gの二酸化マンガンを使ったときを結果を表しているものはどれですか
問2 同じ濃さの過酸化水素35㎤に、0.3gの二酸化マンガンを加えて実験を行うと、発生する酸素の体積は何㎤になりますか
問3 2倍の濃さの過酸化水素15㎤に、0.8gの二酸化マンガンを加えて実験を行うと、発生する酸素の体積は何㎤になりますか
問4 ある濃さの過酸化水素12.5㎤に0.1gの二酸化マンガンを加えて実験を行うと、発生する酸素の体積は90㎤になりました。この過酸化水素の濃さはグラフのときの過酸化水素の濃さの何倍ですか
※表や図は動画内に記載
【受験算数】折り紙を3人には8枚ずつ配り、残りの人には7枚ずつ配ったら、21枚残りました。 そこで、改めて全員に9枚ずつ配ってみましたが、まだ4枚残りました。折り紙の枚数と人数を求めなさい。…

単元:
#算数(中学受験)#文章題#和差算・植木算・分配算・倍数算・年齢算・相当算・つるかめ算#平均算・過不足算・差集め算・消去算
教材:
#SPX#5年算数D-支援#中学受験教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
折り紙を3人には8枚ずつ配り、残りの人には7枚ずつ配ったら、21枚残りました。
そこで、改めて全員に9枚ずつ配ってみましたが、まだ4枚残りました。
折り紙の枚数と人数を求めなさい。
この動画を見る
折り紙を3人には8枚ずつ配り、残りの人には7枚ずつ配ったら、21枚残りました。
そこで、改めて全員に9枚ずつ配ってみましたが、まだ4枚残りました。
折り紙の枚数と人数を求めなさい。
