 福田次郎
福田次郎
 福田次郎
福田次郎
※下の画像部分をクリックすると、先生の紹介ページにリンクします。
福田の数学〜明治大学2024理工学部第1問(1)〜高次方程式と整数解

単元:
#数Ⅱ#大学入試過去問(数学)#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#学校別大学入試過去問解説(数学)#明治大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$k,l,m$ を定数とする。関数 $f(x)=4x^3+kx^2-lx+m$ は次の $3$ つの条件を満たすとする。
・ $k,l,m$ は $0$ 以上の整数である。
・ $x$ に関する方程式 $f(x)=0$ は $\frac{1}{2}$ を解にもつ。
・ $f(x)$ を微分して得られる整式を $f'(x)$ とするとき、 $f'(x)$ を $x+2$ で割ったときの余りは $41$ である。
このとき、$k=\fbox{ア},$ $l=\fbox{イ},$ $m=\fbox{ウ}$ であり、方程式 $f(x)=0$ の $\frac{1}{2}$ 以外の解は $\displaystyle -\frac{\fbox{エ}}{\fbox{オ}}$ と $\fbox{カ}$ である。
この動画を見る
$k,l,m$ を定数とする。関数 $f(x)=4x^3+kx^2-lx+m$ は次の $3$ つの条件を満たすとする。
・ $k,l,m$ は $0$ 以上の整数である。
・ $x$ に関する方程式 $f(x)=0$ は $\frac{1}{2}$ を解にもつ。
・ $f(x)$ を微分して得られる整式を $f'(x)$ とするとき、 $f'(x)$ を $x+2$ で割ったときの余りは $41$ である。
このとき、$k=\fbox{ア},$ $l=\fbox{イ},$ $m=\fbox{ウ}$ であり、方程式 $f(x)=0$ の $\frac{1}{2}$ 以外の解は $\displaystyle -\frac{\fbox{エ}}{\fbox{オ}}$ と $\fbox{カ}$ である。
福田のおもしろ数学247〜複雑な無理方程式の解を1つ見つける

単元:
#関数と極限#関数(分数関数・無理関数・逆関数と合成関数)#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$
5(\sqrt{1-x}+\sqrt{1+x})=6x+8\sqrt{1-x^2}
$の解を1つ求めて下さい。
この動画を見る
$
5(\sqrt{1-x}+\sqrt{1+x})=6x+8\sqrt{1-x^2}
$の解を1つ求めて下さい。
福田のおもしろ数学246〜分数式の極限と区分求積

単元:
#関数と極限#積分とその応用#関数の極限#定積分#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$\displaystyle \lim_{ n \to \infty } \frac{(1+2+…+n)^5}{(1^4+2^4+…+n^4)^2}$
を求めて下さい。
この動画を見る
$\displaystyle \lim_{ n \to \infty } \frac{(1+2+…+n)^5}{(1^4+2^4+…+n^4)^2}$
を求めて下さい。
福田の数学〜明治大学2024全学部統一III第3問〜外サイクロイド曲線と曲線の長さ

単元:
#大学入試過去問(数学)#平面上の曲線#学校別大学入試過去問解説(数学)#媒介変数表示と極座標#明治大学#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
$\boxed{3} a\gt 0$とする。座標平面で、原点$O$を中心とする半径$a$の定円を$C_1$とし、$C_1$と外接する半径$a$の円を$C_2$とする。円$C_2$が定円$C_1$と外接しながらすべることなく転がるとき、$C_2$上の定点$P$が描く曲線を考えたい。始めに$C_2$の中心が$(2a,0)$にあり、$P$が$(a,0)$にあるとする。$C_2$の中心が点$(2a,0)$から原点$O$を中心に反時計回りに$θ$だけ回転した位置にきたとき、$C_1$と$C_2$の接点を通る$C_1$と$C_2$の共通の接線を$l_θ$とする。$l_θ$の方程式は$a=(\boxed{ア})x+(\boxed{イ})y$である。このとき、$P$は直線$l_θ$に関して$(a,0)$と対称な点であるので、$P$の座標を$(x,y)$とすると、$P$の軌跡は$θ$を媒介変数として$x=2a(\boxed{ウ})cosθ+a, y=2a(\boxed{ウ})sinθ$と表される。
$x$と$y$をそれぞれ$θ$で微分すると$\frac{dx}{dθ}=2a(\boxed{エ}),\frac{dy}{dθ}=2a(\boxed{オ})$となるので、$θ$が0から2まで動くとき、$P$が描く曲線の長さは$\boxed{カキ}a$である。
この動画を見る
$\boxed{3} a\gt 0$とする。座標平面で、原点$O$を中心とする半径$a$の定円を$C_1$とし、$C_1$と外接する半径$a$の円を$C_2$とする。円$C_2$が定円$C_1$と外接しながらすべることなく転がるとき、$C_2$上の定点$P$が描く曲線を考えたい。始めに$C_2$の中心が$(2a,0)$にあり、$P$が$(a,0)$にあるとする。$C_2$の中心が点$(2a,0)$から原点$O$を中心に反時計回りに$θ$だけ回転した位置にきたとき、$C_1$と$C_2$の接点を通る$C_1$と$C_2$の共通の接線を$l_θ$とする。$l_θ$の方程式は$a=(\boxed{ア})x+(\boxed{イ})y$である。このとき、$P$は直線$l_θ$に関して$(a,0)$と対称な点であるので、$P$の座標を$(x,y)$とすると、$P$の軌跡は$θ$を媒介変数として$x=2a(\boxed{ウ})cosθ+a, y=2a(\boxed{ウ})sinθ$と表される。
$x$と$y$をそれぞれ$θ$で微分すると$\frac{dx}{dθ}=2a(\boxed{エ}),\frac{dy}{dθ}=2a(\boxed{オ})$となるので、$θ$が0から2まで動くとき、$P$が描く曲線の長さは$\boxed{カキ}a$である。
福田のおもしろ数学245〜3乗根を含む2重根号の計算

福田の数学〜明治大学2024全学部統一III第2問〜複素数平面上の点の移動と確率

単元:
#大学入試過去問(数学)#複素数平面#複素数平面#学校別大学入試過去問解説(数学)#明治大学#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
$i$は虚数単位とし、$\omega =\frac{-1+\sqrt{3}i}{2}$とする。
投げたときに表と裏の出る確率がそれぞれ$\frac{1}{2}$の硬貨を用意する$ z_{0} = 0$ とおき、この硬貨を4回投げて、複素数$z_1, z_2, z_3, z_4$を次の規則により定める。
$n = 1, 2, 3, 4$ に対して、$n$回目に投げたとき、表が出たならば$z_n = \omega z_{n-1}$とし、 裏が出れば$ z_n = z_{n−1}+1$とする。例えば、4回投げた結果、順に「裏、表、裏、 表」と出た場合、$z_{1} = z_{0} + 1 = 1, z_2 = \omega z_1 = \omega, z_{3} = z_{2} + 1 = \omega + 1, z_{4} = \omega z_{3} = \omega ^ 2 + \omega$ となる。
上の規則により$z_1, z_2, z_3, z_4$を定めたとき、$P$を$ z_{4} = 0 $となる確率、$Q$を$ z_{4} = 1$ となる確率、$R$を $z_{4} = \omega + 1$ となる確率とすると$2^4P=\fbox{ア}、2Q=\fbox{イ}, 2R=\fbox{ウ}$である。また、$S$を$|z_4|=1$となる確率、$T$を$|z_4|=2$となる確率とすると$2^4S=\fbox{エ}, 2^4T=\fbox{オ}$である。
この動画を見る
$i$は虚数単位とし、$\omega =\frac{-1+\sqrt{3}i}{2}$とする。
投げたときに表と裏の出る確率がそれぞれ$\frac{1}{2}$の硬貨を用意する$ z_{0} = 0$ とおき、この硬貨を4回投げて、複素数$z_1, z_2, z_3, z_4$を次の規則により定める。
$n = 1, 2, 3, 4$ に対して、$n$回目に投げたとき、表が出たならば$z_n = \omega z_{n-1}$とし、 裏が出れば$ z_n = z_{n−1}+1$とする。例えば、4回投げた結果、順に「裏、表、裏、 表」と出た場合、$z_{1} = z_{0} + 1 = 1, z_2 = \omega z_1 = \omega, z_{3} = z_{2} + 1 = \omega + 1, z_{4} = \omega z_{3} = \omega ^ 2 + \omega$ となる。
上の規則により$z_1, z_2, z_3, z_4$を定めたとき、$P$を$ z_{4} = 0 $となる確率、$Q$を$ z_{4} = 1$ となる確率、$R$を $z_{4} = \omega + 1$ となる確率とすると$2^4P=\fbox{ア}、2Q=\fbox{イ}, 2R=\fbox{ウ}$である。また、$S$を$|z_4|=1$となる確率、$T$を$|z_4|=2$となる確率とすると$2^4S=\fbox{エ}, 2^4T=\fbox{オ}$である。
福田のおもしろ数学244〜1次不等式が常に成り立つ条件

単元:
#数Ⅰ#数と式#一次不等式(不等式・絶対値のある方程式・不等式)#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$0\lt m\lt3$であるすべての$m$に対して$2x-1\lt m(x-2)$が成り立つような$x$の範囲を求めよ。
この動画を見る
$0\lt m\lt3$であるすべての$m$に対して$2x-1\lt m(x-2)$が成り立つような$x$の範囲を求めよ。
福田の数学〜明治大学2024全学部統一III第1問(2)〜定積分の計算

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#学校別大学入試過去問解説(数学)#不定積分・定積分#明治大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\displaystyle \int_{-3}^3 \sqrt{x^2} dx=\fbox{イ}$
この動画を見る
$\displaystyle \int_{-3}^3 \sqrt{x^2} dx=\fbox{イ}$
福田の数学〜明治大学2024全学部統一III第1問(2)〜定積分の計算

単元:
#数Ⅱ#微分法と積分法#不定積分・定積分#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\displaystyle \int_{-3}^3 \sqrt{x^2} dx$
この動画を見る
$\displaystyle \int_{-3}^3 \sqrt{x^2} dx$
福田のおもしろ数学243〜条件を満たす正の整数nの個数

単元:
#数A#整数の性質#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\displaystyle
\sqrt{n^2+2^{100}}
$
が正の整数となるような正の整数nは何個あるか。
この動画を見る
$\displaystyle
\sqrt{n^2+2^{100}}
$
が正の整数となるような正の整数nは何個あるか。
福田の数学〜明治大学2024全学部統一III第1問(1)〜合成関数の微分計算

単元:
#数Ⅱ#微分法と積分法#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\displaystyle
\dfrac{d}{dx}\log{(x+\sqrt{1+x^2})}
$
この動画を見る
$\displaystyle
\dfrac{d}{dx}\log{(x+\sqrt{1+x^2})}
$
福田のおもしろ数学242〜複雑な無理方程式の解

単元:
#数Ⅱ#式と証明#恒等式・等式・不等式の証明#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$x=2+\sqrt{2+\sqrt{2+\sqrt{x}}}$を満たす$x$は?
この動画を見る
$x=2+\sqrt{2+\sqrt{2+\sqrt{x}}}$を満たす$x$は?
福田の数学〜明治大学2024全学部統一IⅡAB第3問〜変わった規則の数列と点列と面積

単元:
#大学入試過去問(数学)#平面上のベクトル#数列#平面上のベクトルと内積#漸化式#学校別大学入試過去問解説(数学)#数学(高校生)#数B#数C
指導講師:
福田次郎
問題文全文(内容文):
整数からなる数列$\{a_n\}~(n=1,2,3,\cdots)$を次の規則1、規則2により定める。
(規則1)$a_1=0,a_2=1$である。
(規則2)$k=1,2,3,\cdots$について、初項から第$2^k$項までの値のそれぞれに$1$を加え、それらすべてを逆の順序にしたものが第$(2^k+1)$項から第$2^{k+1}$項までの値と定める。
例えば、初項と第2項までのそれぞれに$1$を加えて順序を逆にすると$2,1$を得る。これより、初項から第4項までは$0,1,2,1$となる。同様に、これらのそれぞれに$1$を加えて順序を逆にすると$2,3,2,1$となる。これより、初項から第8項までは$0,1,2,1,2,3,2,1$となる。
(1) 以上の規則により得られる数列$\{a_n\}$において、$a_{10}=\boxed{ア}$であり、$a_{16}=\boxed{イ}$である。また第$2^k$項$(k=5,6,7,\cdots)$の値は$\boxed{ウ}$である。
(2) $a_{518}$を求めたい。上記の規則2によれば、$1 \leqq i \leqq 2^k$を満たす$i$に対して$a_1$に$1$を加えた数と第$\boxed{エ}$項が等しいと定めている。実際に、$2^b < 518 < 2^{b+1}$を満たすような整数$b$は$\boxed{オ}$であることに注意すれば、$a_{518}=\boxed{カ}$である。
エの解答群
⓪ $2^k+i-1$ ① $2^k+i$ ② $2^k+i+1$ ③$2^k+2i$ ④ $2^k+2i+1$
⑤ $2^k-i-1$ ⑥ $2^{k+1}-i$ ⑦ $2^{k+1}-i+1$ ⑧ $2^{k+1}-2i-1$ ⑨ $2^{k+1}-2i$
(3) 点$\textrm{P}_k (k=1,2,3,\cdots)$を次のように定める。
数列$\{a_n\}$の初項から第$2^k$項に着目し、$a_n$を4で割った余りにしたがって、ベクトル$\vec{e_n}$を
\begin{eqnarray}
\vec{e_n}
=
\begin{cases}
(1,0) & a_nが4の倍数のとき \\
(0,1) & a_nを4で割った余りが1のとき\\
(-1,0) & a_nを4で割った余りが2のとき\\
(0,-1) & a_nを4で割った余りが3のとき
\end{cases}
\end{eqnarray}
によって定め、点$\textrm{P}_1$の位置ベクトルを$\overrightarrow{\textrm{OP}_1}=\vec{e_1}+\vec{e_2}$とし、点$\textrm{P}_k (k=2,3,4,\cdots)$の位置ベクトルを$\overrightarrow{\textrm{OP}_k}=\vec{e_1}+\vec{e_2}+\vec{e_3}+\cdots+\vec{e_{2^k}}$とする。たとえば、$\overrightarrow{\textrm{OP}_1}=(1,0)+(0,1)+(-1,0)+(0,1)=(0,2)$である。$\{a_n\}$を定める規則に注目すると、$|\overrightarrow{\textrm{OP}_{k+1}}|$は$|\overrightarrow{\textrm{OP}_{k}}|$の$\boxed{キ}$倍であり、$\angle{\textrm{P}_k\textrm{OP}_{k+1}}=\boxed{ク}$である。このことから$\overrightarrow{\textrm{OP}_{99}}$は$(\boxed{ケ},\boxed{コ})$である。
キの解答群
⓪ $\dfrac18$ ① $\dfrac14$ ② $\dfrac12$ ③ $\dfrac{\sqrt{2}}2$ ④ $1$
⑤ $\sqrt2$ ⑥ $2$ ⑦ $2\sqrt2$ ⑧ $4$ ⑨ $8$
クの解答群
⓪ $15^{\circ}$ ① $30^{\circ}$ ② $45^{\circ}$ ③ $60^{\circ}$ ④ $75^{\circ}$
⑤ $90^{\circ}$ ⑥ $105^{\circ}$ ⑦ $120^{\circ}$ ⑧ $135^{\circ}$ ⑨ $150^{\circ}$
ケ、コの解答群
⓪ $-2^{99}$ ① $-2^{98}$ ② $-2^{49}$ ③ $-2^{48}$ ④ $0$
⑤ $1$ ⑥ $2^{48}$ ⑦ $2^{49}$ ⑧ $2^{98}$ ⑨ $2^{99}$
この動画を見る
整数からなる数列$\{a_n\}~(n=1,2,3,\cdots)$を次の規則1、規則2により定める。
(規則1)$a_1=0,a_2=1$である。
(規則2)$k=1,2,3,\cdots$について、初項から第$2^k$項までの値のそれぞれに$1$を加え、それらすべてを逆の順序にしたものが第$(2^k+1)$項から第$2^{k+1}$項までの値と定める。
例えば、初項と第2項までのそれぞれに$1$を加えて順序を逆にすると$2,1$を得る。これより、初項から第4項までは$0,1,2,1$となる。同様に、これらのそれぞれに$1$を加えて順序を逆にすると$2,3,2,1$となる。これより、初項から第8項までは$0,1,2,1,2,3,2,1$となる。
(1) 以上の規則により得られる数列$\{a_n\}$において、$a_{10}=\boxed{ア}$であり、$a_{16}=\boxed{イ}$である。また第$2^k$項$(k=5,6,7,\cdots)$の値は$\boxed{ウ}$である。
(2) $a_{518}$を求めたい。上記の規則2によれば、$1 \leqq i \leqq 2^k$を満たす$i$に対して$a_1$に$1$を加えた数と第$\boxed{エ}$項が等しいと定めている。実際に、$2^b < 518 < 2^{b+1}$を満たすような整数$b$は$\boxed{オ}$であることに注意すれば、$a_{518}=\boxed{カ}$である。
エの解答群
⓪ $2^k+i-1$ ① $2^k+i$ ② $2^k+i+1$ ③$2^k+2i$ ④ $2^k+2i+1$
⑤ $2^k-i-1$ ⑥ $2^{k+1}-i$ ⑦ $2^{k+1}-i+1$ ⑧ $2^{k+1}-2i-1$ ⑨ $2^{k+1}-2i$
(3) 点$\textrm{P}_k (k=1,2,3,\cdots)$を次のように定める。
数列$\{a_n\}$の初項から第$2^k$項に着目し、$a_n$を4で割った余りにしたがって、ベクトル$\vec{e_n}$を
\begin{eqnarray}
\vec{e_n}
=
\begin{cases}
(1,0) & a_nが4の倍数のとき \\
(0,1) & a_nを4で割った余りが1のとき\\
(-1,0) & a_nを4で割った余りが2のとき\\
(0,-1) & a_nを4で割った余りが3のとき
\end{cases}
\end{eqnarray}
によって定め、点$\textrm{P}_1$の位置ベクトルを$\overrightarrow{\textrm{OP}_1}=\vec{e_1}+\vec{e_2}$とし、点$\textrm{P}_k (k=2,3,4,\cdots)$の位置ベクトルを$\overrightarrow{\textrm{OP}_k}=\vec{e_1}+\vec{e_2}+\vec{e_3}+\cdots+\vec{e_{2^k}}$とする。たとえば、$\overrightarrow{\textrm{OP}_1}=(1,0)+(0,1)+(-1,0)+(0,1)=(0,2)$である。$\{a_n\}$を定める規則に注目すると、$|\overrightarrow{\textrm{OP}_{k+1}}|$は$|\overrightarrow{\textrm{OP}_{k}}|$の$\boxed{キ}$倍であり、$\angle{\textrm{P}_k\textrm{OP}_{k+1}}=\boxed{ク}$である。このことから$\overrightarrow{\textrm{OP}_{99}}$は$(\boxed{ケ},\boxed{コ})$である。
キの解答群
⓪ $\dfrac18$ ① $\dfrac14$ ② $\dfrac12$ ③ $\dfrac{\sqrt{2}}2$ ④ $1$
⑤ $\sqrt2$ ⑥ $2$ ⑦ $2\sqrt2$ ⑧ $4$ ⑨ $8$
クの解答群
⓪ $15^{\circ}$ ① $30^{\circ}$ ② $45^{\circ}$ ③ $60^{\circ}$ ④ $75^{\circ}$
⑤ $90^{\circ}$ ⑥ $105^{\circ}$ ⑦ $120^{\circ}$ ⑧ $135^{\circ}$ ⑨ $150^{\circ}$
ケ、コの解答群
⓪ $-2^{99}$ ① $-2^{98}$ ② $-2^{49}$ ③ $-2^{48}$ ④ $0$
⑤ $1$ ⑥ $2^{48}$ ⑦ $2^{49}$ ⑧ $2^{98}$ ⑨ $2^{99}$
福田の数学〜明治大学2024全学部統一IⅡAB第3問〜変わった規則の数列と点列と面積

単元:
#大学入試過去問(数学)#平面上のベクトル#複素数平面#数列#平面上のベクトルと内積#漸化式#複素数平面#学校別大学入試過去問解説(数学)#明治大学#数学(高校生)#数B#数C
指導講師:
福田次郎
問題文全文(内容文):
$\displaystyle
\fcolorbox{#000}{ #fff }{3}
整数からなる数列\{a_n\} \ (n=1,2,3,...)を次の規則1、2により定める。
$
$\displaystyle
(規則1)a_1=0 , \ a_2=1である。
$
$
\displaystyle(規則2)k=1,2,3,...について、初項から第2^{k+1}項までに値のそれぞれに1を加え、\\ それらすべてを逆の順序にしたものが第2^k+1項から第2^{k+1}項までの値と定める。
$
$\displaystyle
(1)以上の規則により得られる数列\{ a_n \}において、a_{10}=\fcolorbox{#000}{ #fff }{$ア \ \ \ $}であり、a_{16}=\fcolorbox{#000}{ #fff }{$イ \ \ \ $}である。 \\
また第2^k項(k=5,6,7,...)の値は\fcolorbox{#000}{ #fff }{$ウ \ \ \ $}である。
$
$\displaystyle
(2)a_{518}を求めたい。上記の規則2によれば、1 \leqq i \leqq 2^kを満たすiに対して、 \\
a_iに1を加えた数と第
\fcolorbox{#000}{ #fff }{$エ \ \ \ $}
項が、等しいと定めている。 \\
実際に、2^b < 518 \leqq 2^{b+1}を満たすような整数bは
\fcolorbox{#000}{ #fff }{$オ \ \ \ $}
であることに注意すれば、a_{518}=
\fcolorbox{#000}{ #fff }{$カ \ \ \ $}
である。
$
$\displaystyle
(3)点O_k(k=1,2,3,...)を次のように定める。\\
数列 \{ a_n \}の初項から第2^k項に着目し、a_nを4で割った余りにしたがって、ベクトル\vec{e_n}を
$
$
\vec{e_n}=
\left\{
\begin{array}{l}
(1,0) \quad a_nが4の倍数のとき \\
(0,1) \quad a_nを4で割った余りが1のとき \\
(-1,0) \quad a_nが4で割った余りが2のとき \\
(0,-1) \quad a_nを4で割った余りが3のとき
\end{array}
\right.
$
$
\displaystyle
によって定め、\\
点P_1の位置ベクトルを\overrightarrow{OP_1}=\vec{e_1}+\vec{e_2}とし、\\
点P_k(k=2,3,4,...)の位置ベクトルを\\
\overrightarrow{OP_k}=\vec{e_1}+\vec{e_2}+\vec{e_3}+...+\vec{e_{2^k}}とする。\\
たとえば、 \\
\overrightarrow{OP_w}=(1,0)+(0,1)+(-1,0)+(0,1)=(0,2)である。\\
\{a_n\}を定める規則に注目すると、 \\
\overrightarrow{OP_{k+1}} は \overrightarrow{OP_k} の\fcolorbox{#000}{ #fff }{$キ \ \ \ $}倍であり、\\
\angle P_kOP_{k+1}=\fcolorbox{#000}{ #fff }{$ク \ \ \ $}である。\\
このことから\\
\overrightarrow{OP_{99}}=(\fcolorbox{#000}{ #fff }{$ケ \ \ \ $},\fcolorbox{#000}{ #fff }{$コ \ \ \ $})である。
$
この動画を見る
$\displaystyle
\fcolorbox{#000}{ #fff }{3}
整数からなる数列\{a_n\} \ (n=1,2,3,...)を次の規則1、2により定める。
$
$\displaystyle
(規則1)a_1=0 , \ a_2=1である。
$
$
\displaystyle(規則2)k=1,2,3,...について、初項から第2^{k+1}項までに値のそれぞれに1を加え、\\ それらすべてを逆の順序にしたものが第2^k+1項から第2^{k+1}項までの値と定める。
$
$\displaystyle
(1)以上の規則により得られる数列\{ a_n \}において、a_{10}=\fcolorbox{#000}{ #fff }{$ア \ \ \ $}であり、a_{16}=\fcolorbox{#000}{ #fff }{$イ \ \ \ $}である。 \\
また第2^k項(k=5,6,7,...)の値は\fcolorbox{#000}{ #fff }{$ウ \ \ \ $}である。
$
$\displaystyle
(2)a_{518}を求めたい。上記の規則2によれば、1 \leqq i \leqq 2^kを満たすiに対して、 \\
a_iに1を加えた数と第
\fcolorbox{#000}{ #fff }{$エ \ \ \ $}
項が、等しいと定めている。 \\
実際に、2^b < 518 \leqq 2^{b+1}を満たすような整数bは
\fcolorbox{#000}{ #fff }{$オ \ \ \ $}
であることに注意すれば、a_{518}=
\fcolorbox{#000}{ #fff }{$カ \ \ \ $}
である。
$
$\displaystyle
(3)点O_k(k=1,2,3,...)を次のように定める。\\
数列 \{ a_n \}の初項から第2^k項に着目し、a_nを4で割った余りにしたがって、ベクトル\vec{e_n}を
$
$
\vec{e_n}=
\left\{
\begin{array}{l}
(1,0) \quad a_nが4の倍数のとき \\
(0,1) \quad a_nを4で割った余りが1のとき \\
(-1,0) \quad a_nが4で割った余りが2のとき \\
(0,-1) \quad a_nを4で割った余りが3のとき
\end{array}
\right.
$
$
\displaystyle
によって定め、\\
点P_1の位置ベクトルを\overrightarrow{OP_1}=\vec{e_1}+\vec{e_2}とし、\\
点P_k(k=2,3,4,...)の位置ベクトルを\\
\overrightarrow{OP_k}=\vec{e_1}+\vec{e_2}+\vec{e_3}+...+\vec{e_{2^k}}とする。\\
たとえば、 \\
\overrightarrow{OP_w}=(1,0)+(0,1)+(-1,0)+(0,1)=(0,2)である。\\
\{a_n\}を定める規則に注目すると、 \\
\overrightarrow{OP_{k+1}} は \overrightarrow{OP_k} の\fcolorbox{#000}{ #fff }{$キ \ \ \ $}倍であり、\\
\angle P_kOP_{k+1}=\fcolorbox{#000}{ #fff }{$ク \ \ \ $}である。\\
このことから\\
\overrightarrow{OP_{99}}=(\fcolorbox{#000}{ #fff }{$ケ \ \ \ $},\fcolorbox{#000}{ #fff }{$コ \ \ \ $})である。
$
福田のおもしろ数学241〜e^πとπ^eの大小

福田のおもしろ数学241〜e^πとπ^eの大小

福田の数学〜明治大学2024全学部統一IⅡAB第2問〜高次方程式の解と面積

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#学校別大学入試過去問解説(数学)#面積、体積#明治大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$x$についての関数$f(x), g(x), h(x)$を$f(x) = 4x^4, g(x) = 12x + 8, h(x) = 4x^2+1$により定める。座標平面上で曲線 $y = f(x)$と直線$y=g(x)$は、異なる2点で交わる。それら交点の$x$座標を$a, b$ ($a \lt b$)とする。
(1) $f(x)+h(x) = (\fbox{ ア }x^2+\fbox{ イ })^2, g(x)+h(x) = (\fbox{ ウ }x+\fbox{ エ })^2$である。
(2) $a+b=\fbox{ オ }, b-a=\sqrt{ \fbox{ カ } }$である。
この動画を見る
$x$についての関数$f(x), g(x), h(x)$を$f(x) = 4x^4, g(x) = 12x + 8, h(x) = 4x^2+1$により定める。座標平面上で曲線 $y = f(x)$と直線$y=g(x)$は、異なる2点で交わる。それら交点の$x$座標を$a, b$ ($a \lt b$)とする。
(1) $f(x)+h(x) = (\fbox{ ア }x^2+\fbox{ イ })^2, g(x)+h(x) = (\fbox{ ウ }x+\fbox{ エ })^2$である。
(2) $a+b=\fbox{ オ }, b-a=\sqrt{ \fbox{ カ } }$である。
福田の数学〜明治大学2024全学部統一IⅡAB第2問〜高次方程式の解と面積

単元:
#数Ⅱ#微分法と積分法#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$
\fcolorbox{#000}{ #fff }{2}
$
$
xについての関数f(x), g(x), h(x)を
$
$
f(x) = 4x ^ 4 , \quad g(x) = 12x + 8 h(x) = 4x ^ 2 + 1
$
$
により定める。座標平面上で曲線 y = f (x)と直線 y = g(x)は、異なる2点で交わる。それら交点の座標をそれぞれa, b(ただしa < b)とする。
$
$
(1) f(x)+h(x) = (
\fcolorbox{#000}{ #fff }{$ア \ \ $}
x² +
\fcolorbox{#000}{ #fff }{$イ \ \ $}
)², g(x)+h(x) = (
\fcolorbox{#000}{ #fff }{$ウ \ \ $}
x+
\fcolorbox{#000}{ #fff }{$エ \ \ $}
)^2 である。
$
$
(2) a + b =
\fcolorbox{#000}{ #fff }{$オ \ \ $}
b - a = \sqrt{
\fcolorbox{#000}{ #fff }{$カ \ \ $}}
である。
$
$
(3) x = a, \ x = bはx^5 =
\fcolorbox{#000}{ #fff }{$カ \ \ $}
x +
\fcolorbox{#000}{ #fff }{$ク \ \ $}
を満たすので、 b ^ 5 - a ^ 5 =
\fcolorbox{#000}{ #fff }{$ケ \ \ $}
\sqrt{
\fcolorbox{#000}{ #fff }{$コ \ \ $}}
である。
$
$
(4) 座標平面上で曲線y = f(x) と直線y = g(x) で囲まれる図形の面積は
\fcolorbox{#000}{ #fff }{$サシ \ \ \ \ \ $}
\sqrt{\fcolorbox{#000}{ #fff }{$ス \ \ $}}
である。
$
この動画を見る
$
\fcolorbox{#000}{ #fff }{2}
$
$
xについての関数f(x), g(x), h(x)を
$
$
f(x) = 4x ^ 4 , \quad g(x) = 12x + 8 h(x) = 4x ^ 2 + 1
$
$
により定める。座標平面上で曲線 y = f (x)と直線 y = g(x)は、異なる2点で交わる。それら交点の座標をそれぞれa, b(ただしa < b)とする。
$
$
(1) f(x)+h(x) = (
\fcolorbox{#000}{ #fff }{$ア \ \ $}
x² +
\fcolorbox{#000}{ #fff }{$イ \ \ $}
)², g(x)+h(x) = (
\fcolorbox{#000}{ #fff }{$ウ \ \ $}
x+
\fcolorbox{#000}{ #fff }{$エ \ \ $}
)^2 である。
$
$
(2) a + b =
\fcolorbox{#000}{ #fff }{$オ \ \ $}
b - a = \sqrt{
\fcolorbox{#000}{ #fff }{$カ \ \ $}}
である。
$
$
(3) x = a, \ x = bはx^5 =
\fcolorbox{#000}{ #fff }{$カ \ \ $}
x +
\fcolorbox{#000}{ #fff }{$ク \ \ $}
を満たすので、 b ^ 5 - a ^ 5 =
\fcolorbox{#000}{ #fff }{$ケ \ \ $}
\sqrt{
\fcolorbox{#000}{ #fff }{$コ \ \ $}}
である。
$
$
(4) 座標平面上で曲線y = f(x) と直線y = g(x) で囲まれる図形の面積は
\fcolorbox{#000}{ #fff }{$サシ \ \ \ \ \ $}
\sqrt{\fcolorbox{#000}{ #fff }{$ス \ \ $}}
である。
$
福田のおもしろ数学240〜e^πが22より大きい証明

福田の数学〜明治大学2024全学部統一IⅡAB第1問(5)〜要素の個数の数え上げ

単元:
#数A#場合の数と確率#場合の数#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$(5)正の整数のうち、3の場椅子であるか、または10進法で表した時に3を含む$$ような数の集合を考える。この集合の要素を小さい順に並べた数列を考える。$$このとき、999は第\fcolorbox{black}{ White }{ニ}項である。$
$ニの解答群$
$(0)\ 333\ (1)\ 396\ (2)\ 414\ (3)\ 459\ (4)\ 495$
$(5)\ 513\ (6)\ 558\ (7)\ 612\ (8)\ 693\ (9)\ 756$
この動画を見る
$(5)正の整数のうち、3の場椅子であるか、または10進法で表した時に3を含む$$ような数の集合を考える。この集合の要素を小さい順に並べた数列を考える。$$このとき、999は第\fcolorbox{black}{ White }{ニ}項である。$
$ニの解答群$
$(0)\ 333\ (1)\ 396\ (2)\ 414\ (3)\ 459\ (4)\ 495$
$(5)\ 513\ (6)\ 558\ (7)\ 612\ (8)\ 693\ (9)\ 756$
福田の数学〜明治大学2024全学部統一IⅡAB第1問(4)〜図形の計量
単元:
#数Ⅰ#図形と計量#三角比(三角比・拡張・相互関係・単位円)#三角比への応用(正弦・余弦・面積)#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
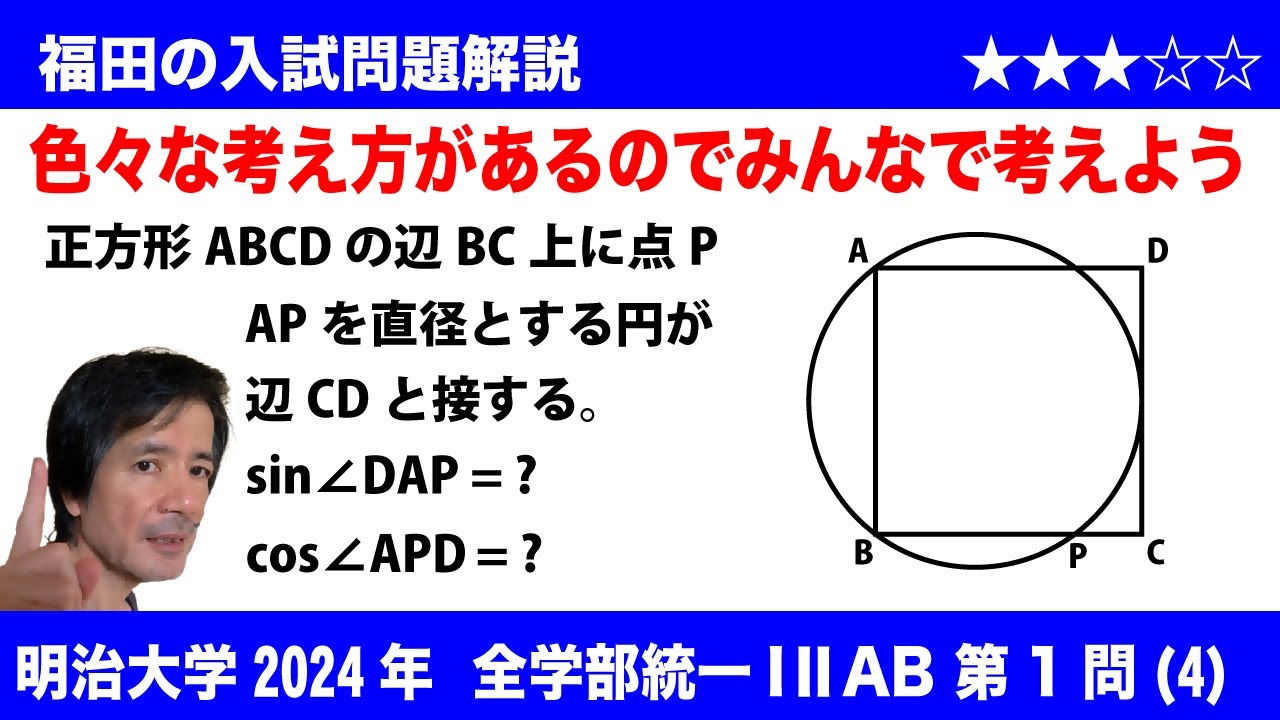
平面上に正方形ABCD (※図は動画内参照) がある。点Pが辺BC上にあり、線分APを直径とする円が辺CDと接するものとする。このとき $\cos{\angle\mathrm{DAP}}=\frac{\fbox{セ}}{\fbox{ソ}}$ であり、また $\sin{\angle\mathrm{APD}}=\frac{\fbox{タチ}\sqrt{\fbox{ツテ}}}{\fbox{トナ}}$ である。
この動画を見る
平面上に正方形ABCD (※図は動画内参照) がある。点Pが辺BC上にあり、線分APを直径とする円が辺CDと接するものとする。このとき $\cos{\angle\mathrm{DAP}}=\frac{\fbox{セ}}{\fbox{ソ}}$ であり、また $\sin{\angle\mathrm{APD}}=\frac{\fbox{タチ}\sqrt{\fbox{ツテ}}}{\fbox{トナ}}$ である。
福田のおもしろ数学238〜4つの放物線で囲まれた図形の面積

福田の数学〜明治大学2024全学部統一IⅡAB第1問(3)〜平均と分散

単元:
#数Ⅰ#データの分析#データの分析#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
次のデータは、ある7人制ラグビーチームの7人の選手の身長を調べたものである。
$181,\,185,\,184,\,176,\,172,\,x,\,y$
このデータの平均が$177$、分散が$40$のとき、$x < y$ とすると$x=\fbox{シ},\,y=\fbox{ス}$である。
この動画を見る
次のデータは、ある7人制ラグビーチームの7人の選手の身長を調べたものである。
$181,\,185,\,184,\,176,\,172,\,x,\,y$
このデータの平均が$177$、分散が$40$のとき、$x < y$ とすると$x=\fbox{シ},\,y=\fbox{ス}$である。
福田のおもしろ数学237〜区分求積法の考え方

単元:
#積分とその応用#定積分#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$$\displaystyle \lim_{ n \to \infty }\displaystyle \sum_{k=n}^{2n} \frac{1}{k}$$を求めよ。
この動画を見る
$$\displaystyle \lim_{ n \to \infty }\displaystyle \sum_{k=n}^{2n} \frac{1}{k}$$を求めよ。
福田の数学〜明治大学2024全学部統一IⅡAB第1問(2)〜対数不等式

単元:
#数Ⅱ#大学入試過去問(数学)#指数関数と対数関数#対数関数#学校別大学入試過去問解説(数学)#明治大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$x$についての不等式$\left( \log_{ 3 } \frac{x}{8}\right)\cdot\left( \log_{ 2 }8x\right)\leqq \left( \log_{ 3 }2\right)\cdot\left( \log_{ 2 } \frac{8}{x}\right)$を解くと、$\frac{\fbox{ ク }}{\fbox{ ケコ }}\leqq x \leqq \fbox{ サ }$である。
この動画を見る
$x$についての不等式$\left( \log_{ 3 } \frac{x}{8}\right)\cdot\left( \log_{ 2 }8x\right)\leqq \left( \log_{ 3 }2\right)\cdot\left( \log_{ 2 } \frac{8}{x}\right)$を解くと、$\frac{\fbox{ ク }}{\fbox{ ケコ }}\leqq x \leqq \fbox{ サ }$である。
福田のおもしろ数学236〜不等式で表された領域の面積

単元:
#積分とその応用#面積・体積・長さ・速度#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
不等式 $2x^2-2xy+y^2 \leqq 1$ の表す領域の面積を求めよ。
この動画を見る
不等式 $2x^2-2xy+y^2 \leqq 1$ の表す領域の面積を求めよ。
福田の数学〜明治大学2024全学部統一IⅡAB第1問(1)〜接線と法線の方程式

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#接線と増減表・最大値・最小値#学校別大学入試過去問解説(数学)#明治大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
座標平面上の放物線 $y=2x^2-1$ を考える。 $t$ を $0$ でない定数とするとき、放物線上の点 $\mathrm{P}(t,2t^2-1)$ における接線 $l$ の方程式は
$y=\fbox{ア}x $$- \fbox{イ}t^2 $$- \fbox{ウ}$
である。点 $\mathrm{P}$ を通りこの接線 $l$ に直交する直線を点 $\mathrm{P}$ における法線と呼ぶことにすると、この法線の方程式は
$y=\fbox{エ}x $$+ \fbox{オ}t^2 $$- \frac{\fbox{カ}}{\fbox{キ}}$ である。
ア、エの解答群は動画内参照。
この動画を見る
座標平面上の放物線 $y=2x^2-1$ を考える。 $t$ を $0$ でない定数とするとき、放物線上の点 $\mathrm{P}(t,2t^2-1)$ における接線 $l$ の方程式は
$y=\fbox{ア}x $$- \fbox{イ}t^2 $$- \fbox{ウ}$
である。点 $\mathrm{P}$ を通りこの接線 $l$ に直交する直線を点 $\mathrm{P}$ における法線と呼ぶことにすると、この法線の方程式は
$y=\fbox{エ}x $$+ \fbox{オ}t^2 $$- \frac{\fbox{カ}}{\fbox{キ}}$ である。
ア、エの解答群は動画内参照。
福田の数学〜浜松医科大学2024医学部第4問〜直線に関する対称点と絶対不等式

単元:
#数Ⅱ#大学入試過去問(数学)#図形と方程式#点と直線#軌跡と領域#学校別大学入試過去問解説(数学)#浜松医科大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
正方形の紙 $\alpha$ に下図のように座標軸をとり、 $2$ 点 $\mathrm{A}(0,1),$ $\mathrm{B}(-2,0)$ および、 $2$ 直線 $y=-1,$$x=2$ を定める(図は動画内参照)。以下この $2$ 直線をそれぞれ $l_1,l_2$ と表す。このとき、点 $\mathrm{A}$ を直線 $l_1$ 上の点 $\mathrm{A'}(a,-1)$ に重ねて $\alpha$ を折ったときにできる折り目の直線を $l_3(a)$ とする。ただし、 $\mathrm{A'}$ は $\alpha$ 上にとることとし、また、以下の操作はすべて $\alpha$ 上で行うこととする。以下の問いに答えよ。
$(1)$ 直線 $l_3(a)$ の方程式を、 $a$ を用いて表せ。
$(2)$ 点 $\mathrm{A}$ が直線 $l_1$ 上に位置するように $\alpha$ を折り、そのときできる折り目により、 $\alpha$ を $2$ つに分割する。このとき、点 $\mathrm{A}$ が直線 $l_1$ 上に位置するような、どのような折り方をしても、その折り目に対して常に点 $\mathrm{A}$ と同じ側にある点全体の集合の境界線の方程式を求めよ。
$(3)$ 点 $\mathrm{A}$ が直線 $l_1$ 上の点 $\mathrm{A'}$ に重なると同時に、点 $\mathrm{B}$ が直線 $l_2$ 上の点に重なるように $\alpha$ を折るとき、 $a$ の値を求めよ。
この動画を見る
正方形の紙 $\alpha$ に下図のように座標軸をとり、 $2$ 点 $\mathrm{A}(0,1),$ $\mathrm{B}(-2,0)$ および、 $2$ 直線 $y=-1,$$x=2$ を定める(図は動画内参照)。以下この $2$ 直線をそれぞれ $l_1,l_2$ と表す。このとき、点 $\mathrm{A}$ を直線 $l_1$ 上の点 $\mathrm{A'}(a,-1)$ に重ねて $\alpha$ を折ったときにできる折り目の直線を $l_3(a)$ とする。ただし、 $\mathrm{A'}$ は $\alpha$ 上にとることとし、また、以下の操作はすべて $\alpha$ 上で行うこととする。以下の問いに答えよ。
$(1)$ 直線 $l_3(a)$ の方程式を、 $a$ を用いて表せ。
$(2)$ 点 $\mathrm{A}$ が直線 $l_1$ 上に位置するように $\alpha$ を折り、そのときできる折り目により、 $\alpha$ を $2$ つに分割する。このとき、点 $\mathrm{A}$ が直線 $l_1$ 上に位置するような、どのような折り方をしても、その折り目に対して常に点 $\mathrm{A}$ と同じ側にある点全体の集合の境界線の方程式を求めよ。
$(3)$ 点 $\mathrm{A}$ が直線 $l_1$ 上の点 $\mathrm{A'}$ に重なると同時に、点 $\mathrm{B}$ が直線 $l_2$ 上の点に重なるように $\alpha$ を折るとき、 $a$ の値を求めよ。
福田のおもしろ数学234〜区分求積の公式の変形その2

単元:
#積分とその応用#不定積分#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$\displaystyle \lim_{ n \to \infty } \frac{1}{n} \sum_{k=1}^{n} f(\frac{k}{n}) $$ = \displaystyle \int_0^1 f(x) dx $ である。では、$\displaystyle \lim_{ n \to \infty } \frac{1}{n+1} \sum_{k=n+2}^{4n+1} f(\frac{k}{n})$ は?
この動画を見る
$\displaystyle \lim_{ n \to \infty } \frac{1}{n} \sum_{k=1}^{n} f(\frac{k}{n}) $$ = \displaystyle \int_0^1 f(x) dx $ である。では、$\displaystyle \lim_{ n \to \infty } \frac{1}{n+1} \sum_{k=n+2}^{4n+1} f(\frac{k}{n})$ は?
福田の数学〜浜松医科大学2024医学部第3問〜等式の証明と無限級数の和
単元:
#大学入試過去問(数学)#関数と極限#数列の極限#学校別大学入試過去問解説(数学)#浜松医科大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
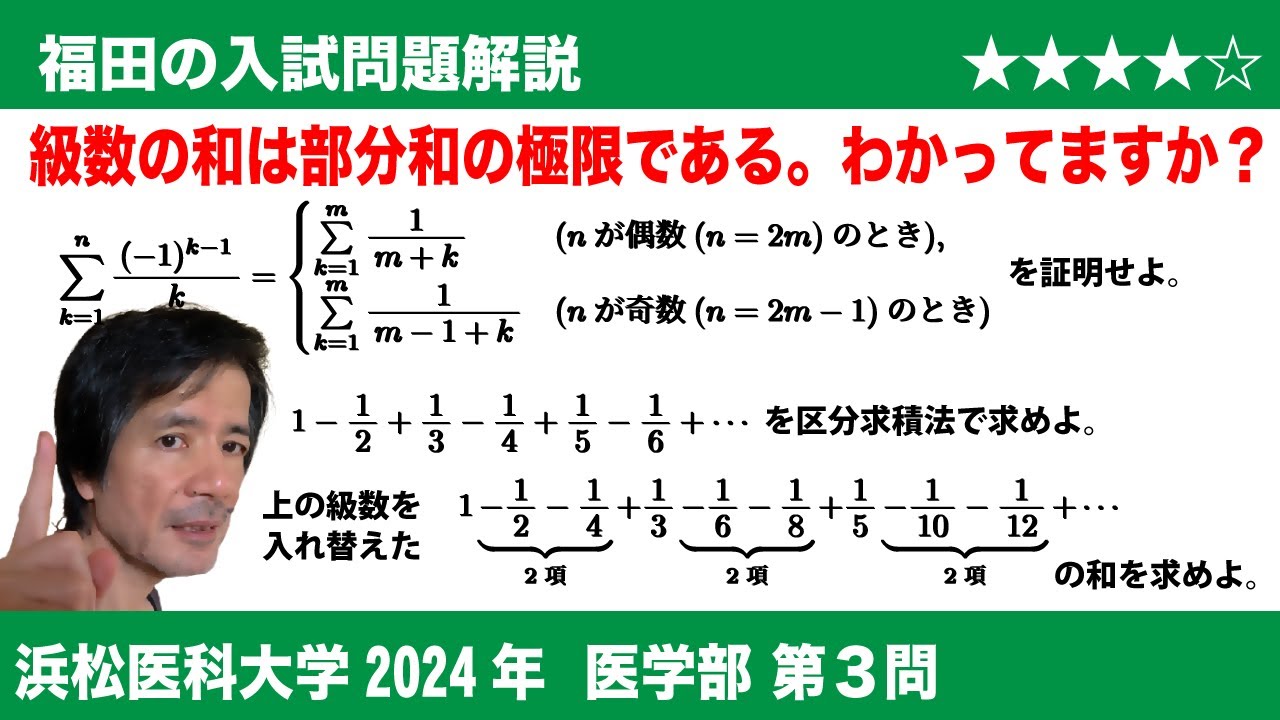
(1) すべての自然数$n$に対して
$\begin{eqnarray}\displaystyle \sum_{k=1}^n \displaystyle \frac{(-1)^{k-1}}{k} =
\begin{cases}
\displaystyle \sum_{k=1}^m \displaystyle \frac{1}{m+k} & (n が偶数(n = 2m)のとき) \\
\displaystyle \sum_{k=1}^m \displaystyle \frac{1}{m-1+k} & ( nが奇数(n = 2m-1)のとき )
\end{cases}
\end{eqnarray}$
を証明せよ.
(2) (1)の左辺において$n \to \infty$として, 区分求積法を用いて無限級数
$1-\frac{1}{2}+\frac{1}{3}-\frac{1}{4}+\frac{1}{5}-\frac{1}{6}+\cdots$
の和の値を求めよ.
(3) (2)の無限級数の項の順序を入れ替えてできる無限級数
$1\underbrace{ -\frac{1}{2}-\frac{1}{4} }_{ 2項 }+\displaystyle \frac{1}{3}\underbrace{ -\frac{1}{6}-\frac{1}{8} }_{ 2項 }+\displaystyle \frac{1}{5}\underbrace{ -\frac{1}{10}-\frac{1}{12} }_{ 2項 }+\cdots$
の和の値を求めよ.
(4) 上の結果からどのようなことが考察されるか.「有限」と「無限」という言葉を用いて述べよ.
この動画を見る
(1) すべての自然数$n$に対して
$\begin{eqnarray}\displaystyle \sum_{k=1}^n \displaystyle \frac{(-1)^{k-1}}{k} =
\begin{cases}
\displaystyle \sum_{k=1}^m \displaystyle \frac{1}{m+k} & (n が偶数(n = 2m)のとき) \\
\displaystyle \sum_{k=1}^m \displaystyle \frac{1}{m-1+k} & ( nが奇数(n = 2m-1)のとき )
\end{cases}
\end{eqnarray}$
を証明せよ.
(2) (1)の左辺において$n \to \infty$として, 区分求積法を用いて無限級数
$1-\frac{1}{2}+\frac{1}{3}-\frac{1}{4}+\frac{1}{5}-\frac{1}{6}+\cdots$
の和の値を求めよ.
(3) (2)の無限級数の項の順序を入れ替えてできる無限級数
$1\underbrace{ -\frac{1}{2}-\frac{1}{4} }_{ 2項 }+\displaystyle \frac{1}{3}\underbrace{ -\frac{1}{6}-\frac{1}{8} }_{ 2項 }+\displaystyle \frac{1}{5}\underbrace{ -\frac{1}{10}-\frac{1}{12} }_{ 2項 }+\cdots$
の和の値を求めよ.
(4) 上の結果からどのようなことが考察されるか.「有限」と「無限」という言葉を用いて述べよ.



