 福田次郎
福田次郎
 福田次郎
福田次郎
※下の画像部分をクリックすると、先生の紹介ページにリンクします。
福田の数学〜立教大学2024年理学部第2問〜反復試行の確率

単元:
#数A#場合の数と確率#確率#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$1$ から $6$ の番号がひとつずつ重複なくつけられた $6$ つの箱がある。このとき、次の試行を行う。
$\fbox{さいころを $1$ つ投げて、出た目の番号のついた箱に玉を $1$ つ入れる。}$
この試行を繰り返し、いずれかの箱に玉が $3$ 個入った時点で終了する。ただし、$1$ 回目の試行を行う前は、どの箱にも玉は $1$ 個も入っていないとする。終了するまでに行った試行の回数を $N$ とする。
$(1)$ $N$ のとりうる最小値 $N_0$ と最大値 $N_1$ をそれぞれ求めよ。
$(2)$ $N=N_{0}$ となる確率を求めよ。
$(3)$ $N=N_{0}+1$ となる確率を求めよ。
$(4)$ 試行を $6$ 回行った時点で、すべての箱に $1$ つずつ玉が入るという事象を $A$ とする。また、$N=N_{1}$ となる事象を $B$ とする。事象 $A$ が起こったときの事象 $B$ が起こる条件付き確率 $P_{A}(B)$ を求めよ。
$(5)$ $N=N_{1}$ となる確率を $P$ とするとき、$6^{8}P$ は整数となる。その値を求めよ。
この動画を見る
$1$ から $6$ の番号がひとつずつ重複なくつけられた $6$ つの箱がある。このとき、次の試行を行う。
$\fbox{さいころを $1$ つ投げて、出た目の番号のついた箱に玉を $1$ つ入れる。}$
この試行を繰り返し、いずれかの箱に玉が $3$ 個入った時点で終了する。ただし、$1$ 回目の試行を行う前は、どの箱にも玉は $1$ 個も入っていないとする。終了するまでに行った試行の回数を $N$ とする。
$(1)$ $N$ のとりうる最小値 $N_0$ と最大値 $N_1$ をそれぞれ求めよ。
$(2)$ $N=N_{0}$ となる確率を求めよ。
$(3)$ $N=N_{0}+1$ となる確率を求めよ。
$(4)$ 試行を $6$ 回行った時点で、すべての箱に $1$ つずつ玉が入るという事象を $A$ とする。また、$N=N_{1}$ となる事象を $B$ とする。事象 $A$ が起こったときの事象 $B$ が起こる条件付き確率 $P_{A}(B)$ を求めよ。
$(5)$ $N=N_{1}$ となる確率を $P$ とするとき、$6^{8}P$ は整数となる。その値を求めよ。
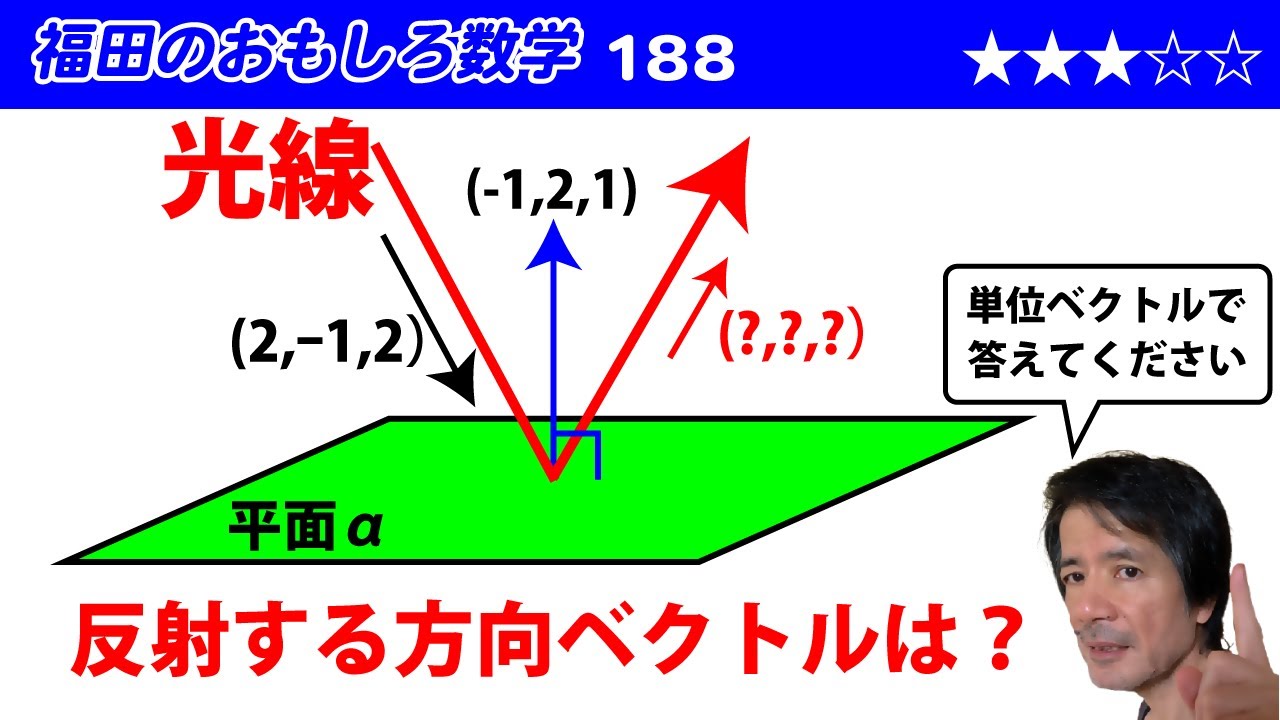
福田のおもしろ数学188〜入射光線の方向ベクトルと平面の法線ベクトルから反射光線の方向ベクトルを知る方法
単元:
#空間ベクトル#空間ベクトル#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
法線ベクトルが $\vec{p}=(-1, \, 2, \, 1)$ である平面 $\alpha$ に、光線が方向ベクトル $\vec{q}=(2, \, -1, \, 2)$ で入射した。このとき反射光線の方向ベクトルを単位ベクトルで求めよ。
この動画を見る
法線ベクトルが $\vec{p}=(-1, \, 2, \, 1)$ である平面 $\alpha$ に、光線が方向ベクトル $\vec{q}=(2, \, -1, \, 2)$ で入射した。このとき反射光線の方向ベクトルを単位ベクトルで求めよ。
福田の数学〜立教大学2024年理学部第1問(5)〜空間ベクトルと直線のベクトル方程式

単元:
#空間ベクトル#空間ベクトル#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
$$座標空間において、点(-1,0,0)を通りベクトル\vec{ a }=(0,1,1)に平行な直線
上の点と、$$$$点(0,0,4)を通り\vec{ b }=(1,2,0)に平行な直線上の点の距離
の最小値は\boxed{ ク }である。$$
この動画を見る
$$座標空間において、点(-1,0,0)を通りベクトル\vec{ a }=(0,1,1)に平行な直線
上の点と、$$$$点(0,0,4)を通り\vec{ b }=(1,2,0)に平行な直線上の点の距離
の最小値は\boxed{ ク }である。$$
福田のおもしろ数学187〜直円錐を平面で切った切り口の面積

福田の数学〜立教大学2024年理学部第1問(4)〜係数が虚数の2次方程式の解

単元:
#数Ⅱ#複素数と方程式#複素数#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$$iを虚数単位とする。複素数zはz^{ 2 }=3-2\sqrt{10 }iを満たし、かつzの実部は正であるとする。$$$$このとき、zの実部は\boxed{ カ }であり、虚部は\boxed{ キ }である。$$
この動画を見る
$$iを虚数単位とする。複素数zはz^{ 2 }=3-2\sqrt{10 }iを満たし、かつzの実部は正であるとする。$$$$このとき、zの実部は\boxed{ カ }であり、虚部は\boxed{ キ }である。$$
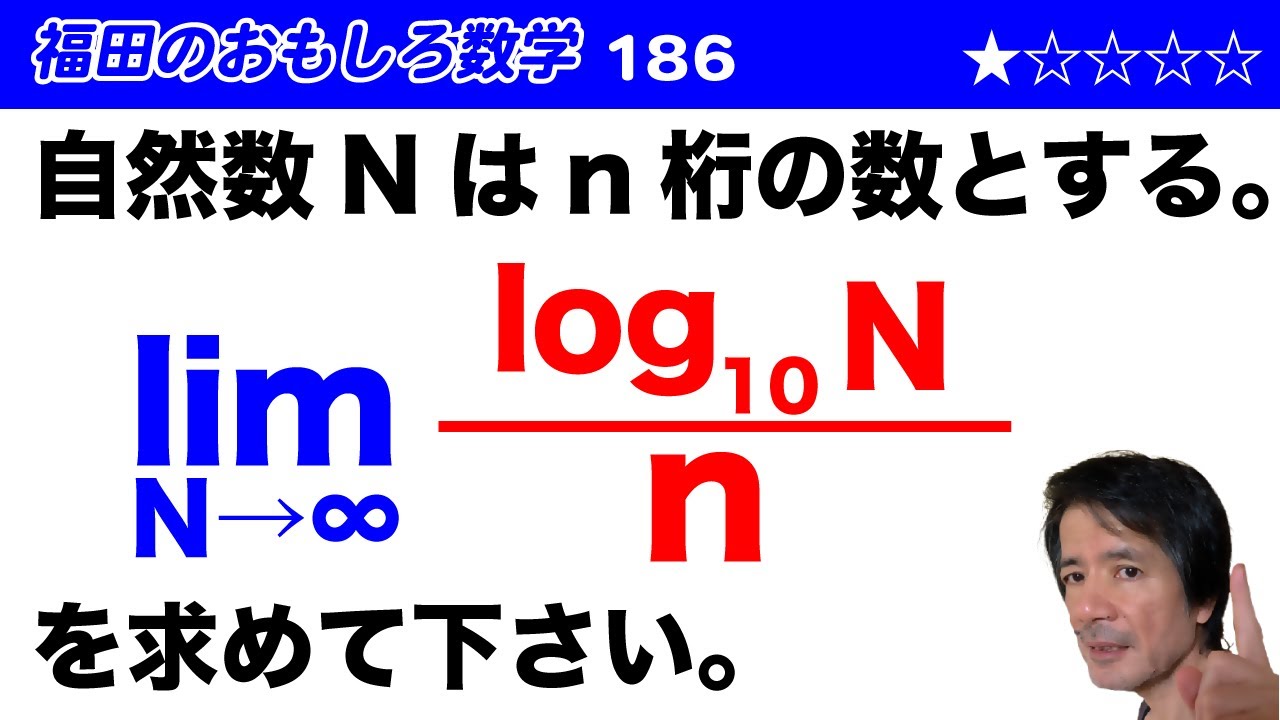
福田のおもしろ数学186〜自然数の桁数と対数の極限
単元:
#関数と極限#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$$Nはn桁の自然数とする。$$
$$\displaystyle \lim_{ n \to \infty }\displaystyle \frac{\log_{ 10 } N}{n}を求めよ。$$
この動画を見る
$$Nはn桁の自然数とする。$$
$$\displaystyle \lim_{ n \to \infty }\displaystyle \frac{\log_{ 10 } N}{n}を求めよ。$$
福田の数学〜立教大学2024年理学部第1問(3)〜対数関数の極値と級数の和

単元:
#関数と極限#積分とその応用#数列の極限#不定積分#定積分#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$$nは自然数とする。
f_{ n }(x)=x^{ \frac{ 1 }{ n }}\log x (x \gt0)がx=a_{ n }で極小値をとるとき、$$
$$a_{ n }=\boxed{ エ }である。このとき、\displaystyle \sum_{i=1}^n a_n=\boxed{ オ }である。$$
この動画を見る
$$nは自然数とする。
f_{ n }(x)=x^{ \frac{ 1 }{ n }}\log x (x \gt0)がx=a_{ n }で極小値をとるとき、$$
$$a_{ n }=\boxed{ エ }である。このとき、\displaystyle \sum_{i=1}^n a_n=\boxed{ オ }である。$$
福田のおもしろ数学185〜8枚の硬貨から1枚の偽物を天秤を使って見抜こう

単元:
#算数(中学受験)#推理と論証#推理と論証
指導講師:
福田次郎
問題文全文(内容文):
8枚の区別のつかない硬貨のなかに、本物よりも軽い偽物が1枚混じっている。
おもりなしの天秤を使って偽物を見つけ出すためには、最小で南海天秤を使えばよいでしょうか。
この動画を見る
8枚の区別のつかない硬貨のなかに、本物よりも軽い偽物が1枚混じっている。
おもりなしの天秤を使って偽物を見つけ出すためには、最小で南海天秤を使えばよいでしょうか。
福田のおもしろ数学185〜8枚の硬貨から1枚の偽物を天秤を使って見抜こう

単元:
#算数(中学受験)#推理と論証#推理と論証
指導講師:
福田次郎
問題文全文(内容文):
\(8\)枚の区別のつかない硬貨のなかに、本物よりも軽い偽物が\(1\)枚混じっている。
おもりなしの天秤を使って偽物を見つけ出すためには、
最小で何回天秤を使えばよいでしょうか。
この動画を見る
\(8\)枚の区別のつかない硬貨のなかに、本物よりも軽い偽物が\(1\)枚混じっている。
おもりなしの天秤を使って偽物を見つけ出すためには、
最小で何回天秤を使えばよいでしょうか。
福田の数学〜立教大学2024年理学部第1問(2)〜17のn乗の1の位

単元:
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#立教大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large{\boxed{1}}$ (2)$17^n$の1の位の数が1になる最小の自然数$n$は$\boxed{\ \ イ\ \ }$である。また、$17^{555}$の1の位の数を求めると、$\boxed{\ \ ウ\ \ }$である。
この動画を見る
$\Large{\boxed{1}}$ (2)$17^n$の1の位の数が1になる最小の自然数$n$は$\boxed{\ \ イ\ \ }$である。また、$17^{555}$の1の位の数を求めると、$\boxed{\ \ ウ\ \ }$である。
福田のおもしろ数学184〜2変数関数の最大最小

単元:
#数Ⅰ#数と式#一次不等式(不等式・絶対値のある方程式・不等式)#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
0≦$x$≦1, 0≦$y$≦1のとき、2変数関数
$f(x,y)$=$5xy-2(x+y)+1$
の最大値$M$、最小値$m$を求めよ。
この動画を見る
0≦$x$≦1, 0≦$y$≦1のとき、2変数関数
$f(x,y)$=$5xy-2(x+y)+1$
の最大値$M$、最小値$m$を求めよ。
福田の数学〜立教大学2024年理学部第1問(1)〜三角方程式の基本

単元:
#数Ⅱ#大学入試過去問(数学)#三角関数#三角関数とグラフ#学校別大学入試過去問解説(数学)#立教大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large{\boxed{1}}$ (1)実数$x$が$3\cos x$=$\sin^2x$ を満たすとき、$\cos x$の値は$\boxed{\ \ ア\ \ }$である。
この動画を見る
$\Large{\boxed{1}}$ (1)実数$x$が$3\cos x$=$\sin^2x$ を満たすとき、$\cos x$の値は$\boxed{\ \ ア\ \ }$である。
福田のおもしろ数学183〜xが−1と1の間の数のときにnx^nが0に収束することの証明

単元:
#関数と極限#数列の極限#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
|$x$|<1 のとき、$\displaystyle\lim_{n \to \infty}nx^n$=0 を示せ。
この動画を見る
|$x$|<1 のとき、$\displaystyle\lim_{n \to \infty}nx^n$=0 を示せ。
福田の数学〜慶應義塾大学2024年経済学部第6問〜3次関数の増減と最大値と面積

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#接線と増減表・最大値・最小値#学校別大学入試過去問解説(数学)#面積、体積#慶應義塾大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large{\boxed{6}}$ $a$,$b$,$p$を実数とする。関数$f(x)$=$x^3$+$ax^2$+$bx$+17 は$x$=$p$で極大値、$x$=$-4p$で極小値をとり、$f(-2p)$=-17 を満たすとする。
(1)$a$,$b$,$p$の値、および$f(x)$の極大値$M$、極大値$m$を、それぞれ求めよ。
(2)(1)で求めた$a$,$b$および0≦$t$≦5 を満たす実数$t$に対して、区間0≦$x$≦$t$ における|$f(x)$|の最大値を$g(t)$とする。$t$の値について場合分けをして、それぞれの場合に$g(t)$を求めよ。
(3)(2)で求めた$g(t)$に対して、定積分$I$=$\displaystyle\int_0^5g(t)dt$ を求めよ。
この動画を見る
$\Large{\boxed{6}}$ $a$,$b$,$p$を実数とする。関数$f(x)$=$x^3$+$ax^2$+$bx$+17 は$x$=$p$で極大値、$x$=$-4p$で極小値をとり、$f(-2p)$=-17 を満たすとする。
(1)$a$,$b$,$p$の値、および$f(x)$の極大値$M$、極大値$m$を、それぞれ求めよ。
(2)(1)で求めた$a$,$b$および0≦$t$≦5 を満たす実数$t$に対して、区間0≦$x$≦$t$ における|$f(x)$|の最大値を$g(t)$とする。$t$の値について場合分けをして、それぞれの場合に$g(t)$を求めよ。
(3)(2)で求めた$g(t)$に対して、定積分$I$=$\displaystyle\int_0^5g(t)dt$ を求めよ。
福田のおもしろ数学182〜2x3x5x7x11x13の10乗の桁数

単元:
#数Ⅱ#大学入試過去問(数学)#指数関数と対数関数#指数関数#学校別大学入試過去問解説(数学)#一橋大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$(2×3×5×7×11×13)^{10}$ の10進法での桁数を求めよ。
この動画を見る
$(2×3×5×7×11×13)^{10}$ の10進法での桁数を求めよ。
福田の数学〜慶應義塾大学2024年経済学部第5問〜ある対数とそれを超えない最大の整数

単元:
#数A#数Ⅱ#大学入試過去問(数学)#整数の性質#指数関数と対数関数#対数関数#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large{\boxed{5}}$ $x$を正の実数とする。$m$と$n$は、それぞれ$m$≦$\displaystyle\log_4\frac{x}{8}$, $n$≦$\displaystyle\log_2\frac{8}{x}$ を満たす最大の整数とし、さらに、$\alpha$=$\displaystyle\log_4\frac{x}{8}$-$m$, $\beta$=$\displaystyle\log_2\frac{8}{x}$-$n$ とおく。
(1)$\log_2x$を、$m$と$\alpha$を用いて表せ。
(2)$2\alpha$+$\beta$ の取りうる値を全て求めよ。
(3)$n$=$m$-1 のとき、$m$と$n$の値を求めよ。
(4)$n$=$m$-1 となるために$x$が満たすべき必要十分条件を求めよ。
この動画を見る
$\Large{\boxed{5}}$ $x$を正の実数とする。$m$と$n$は、それぞれ$m$≦$\displaystyle\log_4\frac{x}{8}$, $n$≦$\displaystyle\log_2\frac{8}{x}$ を満たす最大の整数とし、さらに、$\alpha$=$\displaystyle\log_4\frac{x}{8}$-$m$, $\beta$=$\displaystyle\log_2\frac{8}{x}$-$n$ とおく。
(1)$\log_2x$を、$m$と$\alpha$を用いて表せ。
(2)$2\alpha$+$\beta$ の取りうる値を全て求めよ。
(3)$n$=$m$-1 のとき、$m$と$n$の値を求めよ。
(4)$n$=$m$-1 となるために$x$が満たすべき必要十分条件を求めよ。
福田のおもしろ数学181〜連続する4つの自然数の積は平方数にならないことの証明

福田の数学〜慶應義塾大学2024年経済学部第4問〜正四面体の位置ベクトルと面積体積

単元:
#大学入試過去問(数学)#空間ベクトル#空間ベクトル#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
$\Large{\boxed{4}}$ $p$,$q$を正の実数とし、Oを原点とする座標空間内に3点A(3,$-\sqrt 3$,0),B(3,$\sqrt 3$,0),C($p$,0,$q$)をとる。ただし、四面体OABCは1辺の長さが$2\sqrt 3$の正四面体であるとする。
(1)$p$および$q$の値を求めよ。
以下、点$\displaystyle\left(\frac{3}{2},0,\frac{q}{2}\right)$に関してO,A,B,Cと対称な点を、それぞれD,E,F,Gとする。
(2)直線DGと平面ABCとの交点Hの座標を求めよ。
(3)直線CBと平面DEGとの交点をI、直線CAと平面DFGとの交点をJとする。
四角形CJHIの面積$S$と四角錐G-CJHIの体積$V$を、それぞれ求めよ。
この動画を見る
$\Large{\boxed{4}}$ $p$,$q$を正の実数とし、Oを原点とする座標空間内に3点A(3,$-\sqrt 3$,0),B(3,$\sqrt 3$,0),C($p$,0,$q$)をとる。ただし、四面体OABCは1辺の長さが$2\sqrt 3$の正四面体であるとする。
(1)$p$および$q$の値を求めよ。
以下、点$\displaystyle\left(\frac{3}{2},0,\frac{q}{2}\right)$に関してO,A,B,Cと対称な点を、それぞれD,E,F,Gとする。
(2)直線DGと平面ABCとの交点Hの座標を求めよ。
(3)直線CBと平面DEGとの交点をI、直線CAと平面DFGとの交点をJとする。
四角形CJHIの面積$S$と四角錐G-CJHIの体積$V$を、それぞれ求めよ。
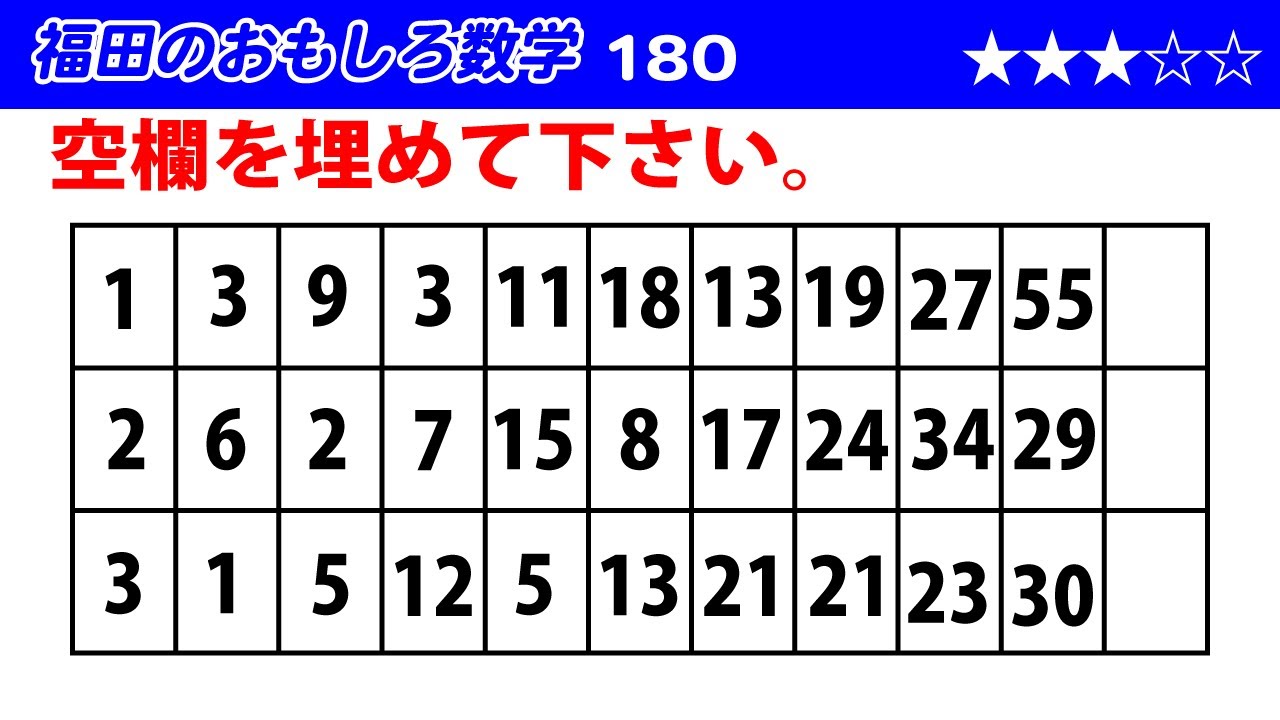
福田のおもしろ数学180〜3行の表に書かれた数値の規則性を考える
単元:
#算数(中学受験)#計算と数の性質#規則性(周期算・方陣算・数列・日暦算・N進法)
指導講師:
福田次郎
問題文全文(内容文):
次の表の空欄を埋めよ。
$\begin{array}{|c|c|c|c|c|c|c|c|c|c|c|}
\hline
1 & 3 & 9 & 3 & 11 & 18 & 13 & 19 & 27 & 55 & \\ \hline
2 & 6 & 2 & 7 & 15 & 8 & 17 & 24 & 34 & 29 & \\ \hline
3 & 1 & 5 & 12 & 5 & 13 & 21 & 21 & 23 & 30 & \\ \hline
\end{array}$
この動画を見る
次の表の空欄を埋めよ。
$\begin{array}{|c|c|c|c|c|c|c|c|c|c|c|}
\hline
1 & 3 & 9 & 3 & 11 & 18 & 13 & 19 & 27 & 55 & \\ \hline
2 & 6 & 2 & 7 & 15 & 8 & 17 & 24 & 34 & 29 & \\ \hline
3 & 1 & 5 & 12 & 5 & 13 & 21 & 21 & 23 & 30 & \\ \hline
\end{array}$
福田の数学〜慶應義塾大学2024年経済学部第3問〜指数関数で定義された数列の漸化式

単元:
#数Ⅱ#大学入試過去問(数学)#指数関数と対数関数#指数関数#対数関数#数列#数列とその和(等差・等比・階差・Σ)#漸化式#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
$\Large{\boxed{3}}$ 実数$a$に対して$f(a)$=$\displaystyle\frac{1}{2}(2^a-2^{-a})$とおく。また、$A$=$2^a$とする。
(1)等式$\displaystyle\left(A-\frac{1}{A}\right)^3$=$\displaystyle\boxed{\ \ ア\ \ }\left(A-\frac{1}{A}\right)^3$-$\displaystyle\boxed{\ \ イ\ \ }\left(A-\frac{1}{A}\right)$ より、実数$a$に対して
$\left\{f(a)\right\}^3$=$\frac{\boxed{\ \ ウ\ \ }}{\boxed{\ \ エ\ \ }}f(3a)$-$\frac{\boxed{\ \ オ\ \ }}{\boxed{\ \ カ\ \ }}f(a)$ ...①が成り立つ。
(2)実数$a$,$b$に対して$f(a)$=$b$が成り立つならば、$A$=$2^a$は2次方程式
$A^2$-$\boxed{\ \ キ\ \ }bA$-$\boxed{\ \ ク\ \ }$=0
を満たす。$2^a$>0より、$a$は$b$を用いて
$a$=$\log_2\left(\boxed{\ \ ケ\ \ }b+\sqrt{b^2+\boxed{\ \ コ\ \ }}\right)$ ...②
と表せる。つまり、任意の実数bに対して$f(a)$=$b$となる実数$a$が、ただ1つに定まる。
以下、数列$\left\{a_n\right\}$に対して$f(a_n)$=$b_n$ ($n$=1,2,3,...)で定まる数列$\left\{b_n\right\}$が、関係式
$4b_{n+1}^3$+$3b_{n+1}$-$b_n$=0 ($n$=1,2,3,...) ...③
を満たすとする。
(3)①と③から$f\left(\boxed{\ \ サ\ \ }a_{n+1}\right)$=$f(a_n)$ ($n$=1,2,3,...)となるので、(2)より、
$a_n$=$\displaystyle\frac{a_1}{\boxed{\ \ シ\ \ }^{n-p}}$ ($n$=1,2,3,...)が得られる。ここで、$p$=$\boxed{\ \ ス\ \ }$である。
(4)$n$≧2に対して、$S_n$=$\displaystyle\sum_{k=2}^n3^{k-1}b_k^3$ とおく。$c_n$=$3^nb_n$ ($n$=1,2,3,...)で定まる数列$\left\{c_n\right\}$の階差数列を用いると、③より、
$S_n$=$\frac{\boxed{\ \ セ\ \ }}{\boxed{\ \ ソ\ \ }}b_1$-$\frac{\boxed{\ \ タ\ \ }^n}{\boxed{\ \ チ\ \ }}b_n$ ($n$=2,3,4,...)
となる。ゆえに、$b_1$=$\displaystyle\frac{4}{3}S_5$-108 が成り立つならば$a_1$=$\boxed{\ \ ツテト\ \ }\log_2\boxed{\ \ ナ\ \ }$ である。
この動画を見る
$\Large{\boxed{3}}$ 実数$a$に対して$f(a)$=$\displaystyle\frac{1}{2}(2^a-2^{-a})$とおく。また、$A$=$2^a$とする。
(1)等式$\displaystyle\left(A-\frac{1}{A}\right)^3$=$\displaystyle\boxed{\ \ ア\ \ }\left(A-\frac{1}{A}\right)^3$-$\displaystyle\boxed{\ \ イ\ \ }\left(A-\frac{1}{A}\right)$ より、実数$a$に対して
$\left\{f(a)\right\}^3$=$\frac{\boxed{\ \ ウ\ \ }}{\boxed{\ \ エ\ \ }}f(3a)$-$\frac{\boxed{\ \ オ\ \ }}{\boxed{\ \ カ\ \ }}f(a)$ ...①が成り立つ。
(2)実数$a$,$b$に対して$f(a)$=$b$が成り立つならば、$A$=$2^a$は2次方程式
$A^2$-$\boxed{\ \ キ\ \ }bA$-$\boxed{\ \ ク\ \ }$=0
を満たす。$2^a$>0より、$a$は$b$を用いて
$a$=$\log_2\left(\boxed{\ \ ケ\ \ }b+\sqrt{b^2+\boxed{\ \ コ\ \ }}\right)$ ...②
と表せる。つまり、任意の実数bに対して$f(a)$=$b$となる実数$a$が、ただ1つに定まる。
以下、数列$\left\{a_n\right\}$に対して$f(a_n)$=$b_n$ ($n$=1,2,3,...)で定まる数列$\left\{b_n\right\}$が、関係式
$4b_{n+1}^3$+$3b_{n+1}$-$b_n$=0 ($n$=1,2,3,...) ...③
を満たすとする。
(3)①と③から$f\left(\boxed{\ \ サ\ \ }a_{n+1}\right)$=$f(a_n)$ ($n$=1,2,3,...)となるので、(2)より、
$a_n$=$\displaystyle\frac{a_1}{\boxed{\ \ シ\ \ }^{n-p}}$ ($n$=1,2,3,...)が得られる。ここで、$p$=$\boxed{\ \ ス\ \ }$である。
(4)$n$≧2に対して、$S_n$=$\displaystyle\sum_{k=2}^n3^{k-1}b_k^3$ とおく。$c_n$=$3^nb_n$ ($n$=1,2,3,...)で定まる数列$\left\{c_n\right\}$の階差数列を用いると、③より、
$S_n$=$\frac{\boxed{\ \ セ\ \ }}{\boxed{\ \ ソ\ \ }}b_1$-$\frac{\boxed{\ \ タ\ \ }^n}{\boxed{\ \ チ\ \ }}b_n$ ($n$=2,3,4,...)
となる。ゆえに、$b_1$=$\displaystyle\frac{4}{3}S_5$-108 が成り立つならば$a_1$=$\boxed{\ \ ツテト\ \ }\log_2\boxed{\ \ ナ\ \ }$ である。
福田のおもしろ数学179〜文字係数の1次不等式の解

福田の数学〜慶應義塾大学2024年経済学部第2問〜確率の基本性質と非復元抽出の条件付き確率

単元:
#数A#大学入試過去問(数学)#場合の数と確率#確率#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large{\boxed{2}}$ 袋の中に、1から9までの番号を重複なく1つずつ記入したカードが9枚入っている。A,B,C,Dの4人のうちDがさいころを投げて、1の目が出たらAが、2または3の目が出たらBが、その他の目が出たらCが、袋の中からカードを1枚引き、カードに記入された番号を記録することを試行という。ただし、1度引いたカードは袋に戻さない。この試行を3回続けて行う。また、1回目の試行前のA,B,Cの点数をそれぞれ0としたうえで、以下の(a),(b)に従い、各回の試行後のA,B,Cの点数を定める。
(a)各回の試行においてカードを引いた人は、その回の試行前の自分の点数に、その回の試行で記録した番号を加え、試行後の点数とする。
(b)各回の試行においてカードを引いていない人は、その回の試行前の自分の点数を、そのまま試行後の点数とする。
(1)1回目の試行後、Bの点数が3の倍数となる確率は$\frac{\boxed{ア}}{\boxed{イ}}$である。ただし、0はすべての整数の倍数である。
(2)2回目の試行後、A,B,Cのうち、1人だけの点数が0である確率は$\frac{\boxed{ウエ}}{\boxed{オカ}}$である。
(3)2回目の試行後のAの点数が5以上となる確率は$\frac{\boxed{キク}}{\boxed{ケコ}}$である。
(4)2回目の試行後のAの点数が5以上であるとき、3回目の試行後のA,B,Cの点数がすべて5以上である条件付き確率は$\frac{\boxed{サシ}}{\boxed{スセソ}}$である。
この動画を見る
$\Large{\boxed{2}}$ 袋の中に、1から9までの番号を重複なく1つずつ記入したカードが9枚入っている。A,B,C,Dの4人のうちDがさいころを投げて、1の目が出たらAが、2または3の目が出たらBが、その他の目が出たらCが、袋の中からカードを1枚引き、カードに記入された番号を記録することを試行という。ただし、1度引いたカードは袋に戻さない。この試行を3回続けて行う。また、1回目の試行前のA,B,Cの点数をそれぞれ0としたうえで、以下の(a),(b)に従い、各回の試行後のA,B,Cの点数を定める。
(a)各回の試行においてカードを引いた人は、その回の試行前の自分の点数に、その回の試行で記録した番号を加え、試行後の点数とする。
(b)各回の試行においてカードを引いていない人は、その回の試行前の自分の点数を、そのまま試行後の点数とする。
(1)1回目の試行後、Bの点数が3の倍数となる確率は$\frac{\boxed{ア}}{\boxed{イ}}$である。ただし、0はすべての整数の倍数である。
(2)2回目の試行後、A,B,Cのうち、1人だけの点数が0である確率は$\frac{\boxed{ウエ}}{\boxed{オカ}}$である。
(3)2回目の試行後のAの点数が5以上となる確率は$\frac{\boxed{キク}}{\boxed{ケコ}}$である。
(4)2回目の試行後のAの点数が5以上であるとき、3回目の試行後のA,B,Cの点数がすべて5以上である条件付き確率は$\frac{\boxed{サシ}}{\boxed{スセソ}}$である。
福田のおもしろ数学178〜ある等式を満たす100個の変数のうちのひとつの変数の最大値

単元:
#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\displaystyle\frac{a_1^2+a_2^2+...+a_{100}^2}{a_1+a_2+...+a_{100}}$=100 を満たす実数$a_1$の最大値を求めてください。
この動画を見る
$\displaystyle\frac{a_1^2+a_2^2+...+a_{100}^2}{a_1+a_2+...+a_{100}}$=100 を満たす実数$a_1$の最大値を求めてください。
福田の数学〜慶應義塾大学2024年経済学部第1問(2)〜三角関数への置き換えによる分数関数の最大最小

単元:
#数Ⅱ#大学入試過去問(数学)#三角関数#加法定理とその応用#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{1}$
(2)$\theta$は|$\theta$|<$\displaystyle\frac{\pi}{2}$の範囲の定数とする。$x$=$\tan\theta$とおくと、$\displaystyle\frac{x}{x^2+1}$=$\frac{\boxed{ク}}{\boxed{ケ}}\sin2\theta$かつ$\displaystyle\frac{1}{x^2+1}$=$\frac{\boxed{コ}}{\boxed{サ}}(\cos2\theta$+1)であるので、$\displaystyle y=\frac{x^2+3x+5}{x^2+1}$とすると、
$\displaystyle y=\frac{\boxed{シ}}{\boxed{ス}}\sin(2\theta+\alpha)$+$\boxed{セ}$
と表せる。ただし、$\cos\alpha$=$\frac{\boxed{ソ}}{\boxed{タ}}$, $\sin\alpha$=$\frac{\boxed{チ}}{\boxed{ツ}}$である。また、|$x$|≦1に対応する$\theta$の範囲が|$\theta$|≦$\displaystyle\frac{\pi}{\boxed{テ}}$であることに注意すると、|$x$|≦1における$y$の取りうる値の最大値は$\frac{\boxed{トナ}}{\boxed{ニ}}$、最小値は$\frac{\boxed{ヌ}}{\boxed{ネ}}$ である。
この動画を見る
$\Large\boxed{1}$
(2)$\theta$は|$\theta$|<$\displaystyle\frac{\pi}{2}$の範囲の定数とする。$x$=$\tan\theta$とおくと、$\displaystyle\frac{x}{x^2+1}$=$\frac{\boxed{ク}}{\boxed{ケ}}\sin2\theta$かつ$\displaystyle\frac{1}{x^2+1}$=$\frac{\boxed{コ}}{\boxed{サ}}(\cos2\theta$+1)であるので、$\displaystyle y=\frac{x^2+3x+5}{x^2+1}$とすると、
$\displaystyle y=\frac{\boxed{シ}}{\boxed{ス}}\sin(2\theta+\alpha)$+$\boxed{セ}$
と表せる。ただし、$\cos\alpha$=$\frac{\boxed{ソ}}{\boxed{タ}}$, $\sin\alpha$=$\frac{\boxed{チ}}{\boxed{ツ}}$である。また、|$x$|≦1に対応する$\theta$の範囲が|$\theta$|≦$\displaystyle\frac{\pi}{\boxed{テ}}$であることに注意すると、|$x$|≦1における$y$の取りうる値の最大値は$\frac{\boxed{トナ}}{\boxed{ニ}}$、最小値は$\frac{\boxed{ヌ}}{\boxed{ネ}}$ である。
福田のおもしろ数学177〜長さ1.5メートルの剣を列車に積み込む方法

単元:
#数学(中学生)#中3数学#三平方の定理
指導講師:
福田次郎
問題文全文(内容文):
あなたは1.5 mの剣を列車に持ち込もうとしましたが車掌に拒否されました。
一辺の最大の寸法が1 mを超すものは持ち込めません。
あなたはどうする?
この動画を見る
あなたは1.5 mの剣を列車に持ち込もうとしましたが車掌に拒否されました。
一辺の最大の寸法が1 mを超すものは持ち込めません。
あなたはどうする?
福田の数学〜慶應義塾大学2024年経済学部第1問(1)〜2次方程式が整数解をもつ条件

単元:
#数A#数Ⅱ#大学入試過去問(数学)#複素数と方程式#整数の性質#ユークリッド互除法と不定方程式・N進法#解と判別式・解と係数の関係#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{1}$ (1)$p$を実数とする。$x$の2次方程式$x^2$-($p$-9)$x$-$p$+1=0 の解は整数$m$<0<$n$が成り立つとする。このとき$mn$+$m$+$n$=$\boxed{\ \ アイ\ \ }$なので、$m$=$\boxed{\ \ ウエ\ \ }$, $n$=$\boxed{\ \ オ\ \ }$, $p$=$\boxed{\ \ カキ\ \ }$ である。
この動画を見る
$\Large\boxed{1}$ (1)$p$を実数とする。$x$の2次方程式$x^2$-($p$-9)$x$-$p$+1=0 の解は整数$m$<0<$n$が成り立つとする。このとき$mn$+$m$+$n$=$\boxed{\ \ アイ\ \ }$なので、$m$=$\boxed{\ \ ウエ\ \ }$, $n$=$\boxed{\ \ オ\ \ }$, $p$=$\boxed{\ \ カキ\ \ }$ である。
福田のおもしろ数学176〜ルートが無限に重なる等式の証明

単元:
#数Ⅱ#式と証明#指数関数と対数関数#恒等式・等式・不等式の証明#指数関数#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\sqrt{x\sqrt{x\sqrt{...}}}$=$x$ を証明してください。ただし$x$は正の実数とする。
この動画を見る
$\sqrt{x\sqrt{x\sqrt{...}}}$=$x$ を証明してください。ただし$x$は正の実数とする。
福田の数学〜慶應義塾大学2024年医学部第4問〜空間に浮かぶ四面体の平面による切り口の面積

単元:
#大学入試過去問(数学)#空間ベクトル#空間ベクトル#積分とその応用#面積・体積・長さ・速度#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)#数C#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{4}$ 座標空間の4点O(0,0,0),A(-3,-1,1),B(2,-2,2),C(3,3,3)を頂点とする四面体OABCの、平面$z$=$t$による切り口を$S_t$とする。
(1)$S_t$は1<$t$<2のとき四角形となり、$t$=1および$t$=2のとき三角形となる。
1<$t$1 となるので、点Eはこの六面体の外にある。
(さ),(し),(す)の選択肢:ABC,ABD,ACD,BCD,OAD,OBD,OCD
(4)1<$t$<2に対して、(3)の六面体を平面$z$=$t$で切った切り口の面積を$U(t)$とすると、$U(t)$は$t$=$\boxed{\ \ (た)\ \ }$(ただし1<$\boxed{\ \ (た)\ \ }$<2)において最大値$\boxed{\ \ (ち)\ \ }$をとる。
この動画を見る
$\Large\boxed{4}$ 座標空間の4点O(0,0,0),A(-3,-1,1),B(2,-2,2),C(3,3,3)を頂点とする四面体OABCの、平面$z$=$t$による切り口を$S_t$とする。
(1)$S_t$は1<$t$<2のとき四角形となり、$t$=1および$t$=2のとき三角形となる。
1<$t$1 となるので、点Eはこの六面体の外にある。
(さ),(し),(す)の選択肢:ABC,ABD,ACD,BCD,OAD,OBD,OCD
(4)1<$t$<2に対して、(3)の六面体を平面$z$=$t$で切った切り口の面積を$U(t)$とすると、$U(t)$は$t$=$\boxed{\ \ (た)\ \ }$(ただし1<$\boxed{\ \ (た)\ \ }$<2)において最大値$\boxed{\ \ (ち)\ \ }$をとる。
福田のおもしろ数学175〜0から10^nまでの数に現れる各桁の数字の総和を求める

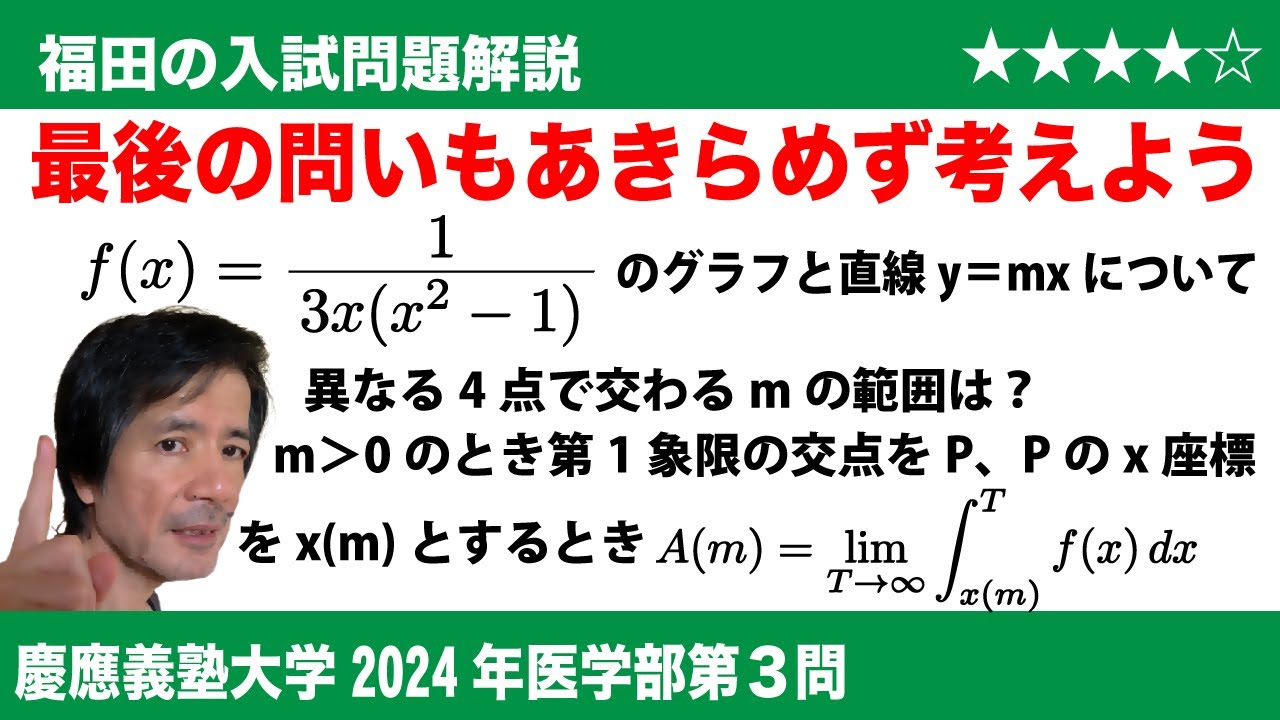
福田の数学〜慶應義塾大学2024年医学部第3問〜四面体の切断面の面積と極限
単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{3}$ -1,0,1以外のすべての実数$x$に対して定義された関数
$f(x)$=$\displaystyle\frac{1}{3x(x^2-1)}$
を考える。
(1)$f(x)$は$x$=$\boxed{\ \ (あ)\ \ }$において極小値$\boxed{\ \ (い)\ \ }$をとり、$x$=$\boxed{\ \ (う)\ \ }$において極大値$\boxed{\ \ (え)\ \ }$をとる。
(2)曲線$y$=$f(x)$の概形を描きなさい。
(3)直線$y$=$mx$が曲線$y$=$f(x)$とちょうど4点で交わるとき、定数$m$の値の範囲は$\boxed{\ \ (お)\ \ }$である。
(4)$a$=$\boxed{\ \ (か)\ \ }$, $b$=$\boxed{\ \ (き)\ \ }$, $c$=$\boxed{\ \ (く)\ \ }$とすると、つぎの恒等式が成り立つ。
$f(x)$=$\displaystyle\frac{a}{x-1}$+$\displaystyle\frac{b}{x}$+$\displaystyle\frac{c}{x+1}$
(5)直線$y$=$mx$ (ただし$m$>0)が曲線$y$=$f(x)$と第1象限において交わる点Pの$x$座標を$x(m)$とし、
$A(m)$=$\displaystyle\lim_{T \to \infty}\int_{x(m)}^Tf(x)dx$
とおいて、$A(m)$を$m$の式で表すと、$A(m)$=$\boxed{\ \ (け)\ \ }$となる。また、原点をO、$\left(x(m),0\right)$を座標とする点をQとし、三角形OPQの面積を$B(m)$とおくと$\displaystyle\lim_{m \to +0}\frac{A(m)}{B(m)}$=$\boxed{\ \ (こ)\ \ }$ となる。
この動画を見る
$\Large\boxed{3}$ -1,0,1以外のすべての実数$x$に対して定義された関数
$f(x)$=$\displaystyle\frac{1}{3x(x^2-1)}$
を考える。
(1)$f(x)$は$x$=$\boxed{\ \ (あ)\ \ }$において極小値$\boxed{\ \ (い)\ \ }$をとり、$x$=$\boxed{\ \ (う)\ \ }$において極大値$\boxed{\ \ (え)\ \ }$をとる。
(2)曲線$y$=$f(x)$の概形を描きなさい。
(3)直線$y$=$mx$が曲線$y$=$f(x)$とちょうど4点で交わるとき、定数$m$の値の範囲は$\boxed{\ \ (お)\ \ }$である。
(4)$a$=$\boxed{\ \ (か)\ \ }$, $b$=$\boxed{\ \ (き)\ \ }$, $c$=$\boxed{\ \ (く)\ \ }$とすると、つぎの恒等式が成り立つ。
$f(x)$=$\displaystyle\frac{a}{x-1}$+$\displaystyle\frac{b}{x}$+$\displaystyle\frac{c}{x+1}$
(5)直線$y$=$mx$ (ただし$m$>0)が曲線$y$=$f(x)$と第1象限において交わる点Pの$x$座標を$x(m)$とし、
$A(m)$=$\displaystyle\lim_{T \to \infty}\int_{x(m)}^Tf(x)dx$
とおいて、$A(m)$を$m$の式で表すと、$A(m)$=$\boxed{\ \ (け)\ \ }$となる。また、原点をO、$\left(x(m),0\right)$を座標とする点をQとし、三角形OPQの面積を$B(m)$とおくと$\displaystyle\lim_{m \to +0}\frac{A(m)}{B(m)}$=$\boxed{\ \ (こ)\ \ }$ となる。



