 ますただ
ますただ
 ますただ
ますただ
※下の画像部分をクリックすると、先生の紹介ページにリンクします。
この積分は難問「もはや積分偏差値70over」 By 英語orドイツ語シはBかHか さん

単元:
#積分とその応用#定積分#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{-1}^{1} \displaystyle \frac{x|x|(2x^2+1)e^{2x^2}}{2x(xe^{x^2}-1)+e^{-x^2}} dx$
この動画を見る
$\displaystyle \int_{-1}^{1} \displaystyle \frac{x|x|(2x^2+1)e^{2x^2}}{2x(xe^{x^2}-1)+e^{-x^2}} dx$
会津大学2014 #定積分 #shorts

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{1} e^x\sqrt{ e^x-1 }\ dx$
出典:2019年会津大学
この動画を見る
$\displaystyle \int_{0}^{1} e^x\sqrt{ e^x-1 }\ dx$
出典:2019年会津大学
大学入試問題#589「一度は解いておきたい良問」 奈良女子大学(2004) #数列

単元:
#大学入試過去問(数学)#数列#数列とその和(等差・等比・階差・Σ)#関数と極限#数列の極限#学校別大学入試過去問解説(数学)#奈良女子大学#数学(高校生)#数B#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$a_1\times a_2\times・・・\times a_n=\displaystyle \frac{1}{(n+1)(n!)^2}$のとき
$\displaystyle \sum_{n=1}^\infty a_n$を求めよ
出典:2004年奈良女子大学 入試問題
この動画を見る
$a_1\times a_2\times・・・\times a_n=\displaystyle \frac{1}{(n+1)(n!)^2}$のとき
$\displaystyle \sum_{n=1}^\infty a_n$を求めよ
出典:2004年奈良女子大学 入試問題
大学入試問題#588「なんか似た問題解いたことある。」 横浜市立大学(2020) #方程式

単元:
#数Ⅱ#大学入試過去問(数学)#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#学校別大学入試過去問解説(数学)#数学(高校生)#横浜市立大学
指導講師:
ますただ
問題文全文(内容文):
$x^4-8x^3+17x^2-8x+1=0$
出典:2020年横浜市立大学医学部 入試問題
この動画を見る
$x^4-8x^3+17x^2-8x+1=0$
出典:2020年横浜市立大学医学部 入試問題
大学入試問題#587「たぶん基本問題」 広島市立大学(2013) #不定積分
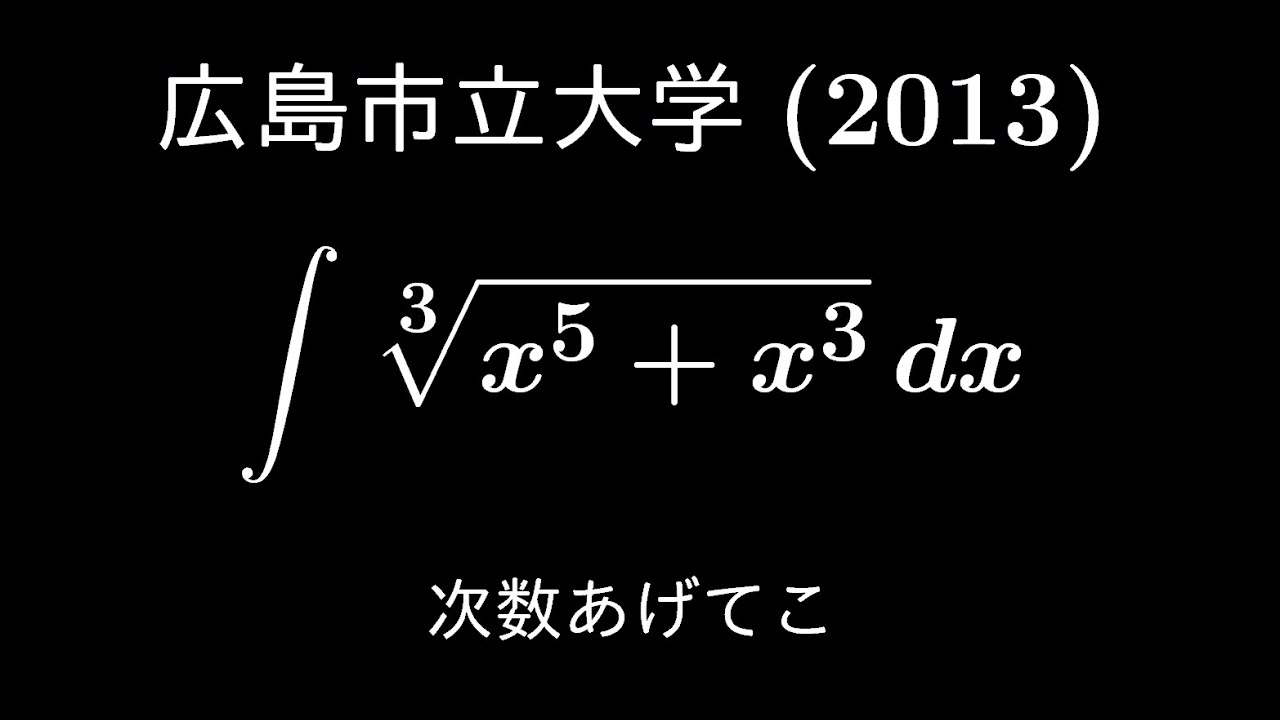
単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#広島市立大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int \sqrt[3]{ x^5+x^3 }\ dx$
出典:2013年広島市立大学 入試問題
この動画を見る
$\displaystyle \int \sqrt[3]{ x^5+x^3 }\ dx$
出典:2013年広島市立大学 入試問題
大学入試問題#587「落とせない問題」 京都大学(1960) #方程式

単元:
#数Ⅱ#大学入試過去問(数学)#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$x^3+x+2=0$のとき
$x^5-x$の値を求めよ
出典:1960年京都大学 入試問題
この動画を見る
$x^3+x+2=0$のとき
$x^5-x$の値を求めよ
出典:1960年京都大学 入試問題
広島市立大学 2016 #不定積分 #Shorts

単元:
#大学入試過去問(数学)#積分とその応用#不定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#広島市立大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int \displaystyle \frac{\cos^3\ x}{\sin^2\ x} dx$
出典:2016年広島市立大学
この動画を見る
$\displaystyle \int \displaystyle \frac{\cos^3\ x}{\sin^2\ x} dx$
出典:2016年広島市立大学
大学入試問題#586「見た目が美しい」 広島市立大学(2009) #不定積分

単元:
#大学入試過去問(数学)#積分とその応用#不定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#広島市立大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int \displaystyle \frac{dx}{x+\sqrt{ x }}$
出典:2009年広島市立大学 入試問題
この動画を見る
$\displaystyle \int \displaystyle \frac{dx}{x+\sqrt{ x }}$
出典:2009年広島市立大学 入試問題
大学入試問題#585「気付けば暗算」 同志社大学(2004) #極限
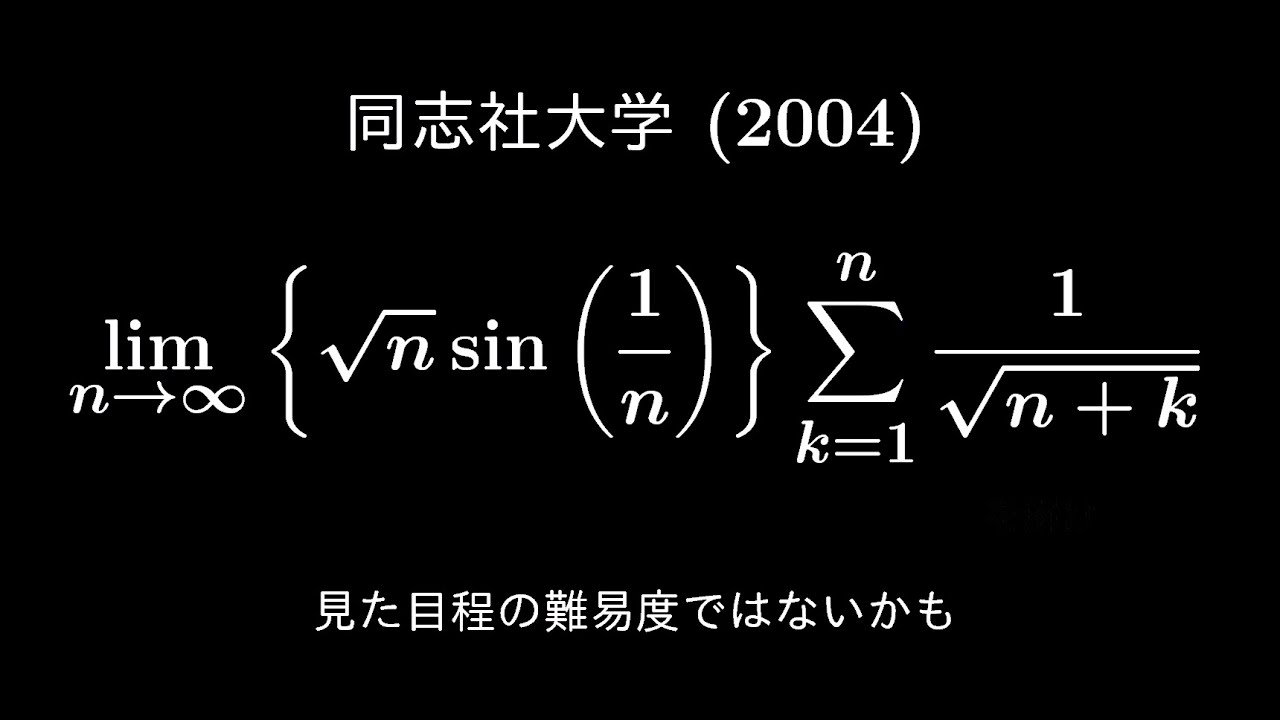
単元:
#大学入試過去問(数学)#関数と極限#積分とその応用#関数の極限#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#同志社大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \lim_{ n \to \infty } \{\sqrt{ n }\sin(\displaystyle \frac{1}{n})\}\displaystyle \sum_{k=1}^n \displaystyle \frac{1}{\sqrt{ n+k }}$
出典:2004年同志社大学 入試問題
この動画を見る
$\displaystyle \lim_{ n \to \infty } \{\sqrt{ n }\sin(\displaystyle \frac{1}{n})\}\displaystyle \sum_{k=1}^n \displaystyle \frac{1}{\sqrt{ n+k }}$
出典:2004年同志社大学 入試問題
大学入試問題#584「これは落としたくない!!」 京都帝国大学(1937) #不定積分

単元:
#大学入試過去問(数学)#積分とその応用#不定積分#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int \displaystyle \frac{2x+3}{x^3+x^2-2x} dx$
出典:1937年京都帝国大学 入試問題
この動画を見る
$\displaystyle \int \displaystyle \frac{2x+3}{x^3+x^2-2x} dx$
出典:1937年京都帝国大学 入試問題
広島市立大学(2009) #不定積分 #Shorts

単元:
#大学入試過去問(数学)#積分とその応用#不定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#広島市立大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int log(1+2x) dx$
出典:2009年広島市立大学
この動画を見る
$\displaystyle \int log(1+2x) dx$
出典:2009年広島市立大学
#58数検1級1次「ぱっと見はちょろそうだけど・・・」 #方程式

単元:
#数Ⅱ#数学検定・数学甲子園・数学オリンピック等#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#数学検定#数学検定1級#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
方程式
$x^6-14x^4+17x^2-4=0$を解け。
出典:数検1級1次
この動画を見る
方程式
$x^6-14x^4+17x^2-4=0$を解け。
出典:数検1級1次
大学入試問題#582「ガチンコでぶつかると危険」 東京帝国大学(1946) 不定積分

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#東京大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int \displaystyle \frac{dx}{x-\sqrt{ x^2-1 }}$
出典:1946年東京帝国大学 入試問題
この動画を見る
$\displaystyle \int \displaystyle \frac{dx}{x-\sqrt{ x^2-1 }}$
出典:1946年東京帝国大学 入試問題
#57数検準1級1次「ほぼ1本道」 #極限

単元:
#数学検定・数学甲子園・数学オリンピック等#関数と極限#関数の極限#数学検定#数学検定準1級#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \lim_{ x \to 1 } \displaystyle \frac{x^2+2x-3}{\sqrt[ 3 ]{ x }-1}$
出典:数検準1級1次
この動画を見る
$\displaystyle \lim_{ x \to 1 } \displaystyle \frac{x^2+2x-3}{\sqrt[ 3 ]{ x }-1}$
出典:数検準1級1次
東邦大学医学部(2011) #Shorts #King_property #キングプロパティ

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#東邦大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{\frac{\pi}{2}} \displaystyle \frac{\cos\ x}{\sin\ x+\cos\ x} dx$
出典:2011年東邦大学医学部 入試問題
この動画を見る
$\displaystyle \int_{0}^{\frac{\pi}{2}} \displaystyle \frac{\cos\ x}{\sin\ x+\cos\ x} dx$
出典:2011年東邦大学医学部 入試問題
#57数検準1級1次 #定積分

単元:
#数学検定・数学甲子園・数学オリンピック等#積分とその応用#定積分#数学検定#数学検定準1級#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{2} (\displaystyle \frac{x^2}{2}+3x)e^{\frac{x}{2}}\ dx$
出典:数検準1級1次
この動画を見る
$\displaystyle \int_{0}^{2} (\displaystyle \frac{x^2}{2}+3x)e^{\frac{x}{2}}\ dx$
出典:数検準1級1次
大学入試問題#581「最後まで落ち着いて!」 東京帝国大学(1940) #不定積分

単元:
#大学入試過去問(数学)#積分とその応用#不定積分#学校別大学入試過去問解説(数学)#東京大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int \displaystyle \frac{3x^2-3x+2}{x^3-3x^2+x-3} dx$
出典:1940年東京帝国大学 入試問題
この動画を見る
$\displaystyle \int \displaystyle \frac{3x^2-3x+2}{x^3-3x^2+x-3} dx$
出典:1940年東京帝国大学 入試問題
#56数検1級1次 過去問 #4次方程式

単元:
#数Ⅱ#数学検定・数学甲子園・数学オリンピック等#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#数学検定#数学検定1級#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
方程式
$x^4-4x-1=0$の実数解を求めよ
出典:数検1級1次
この動画を見る
方程式
$x^4-4x-1=0$の実数解を求めよ
出典:数検1級1次
大学入試問題#580「これは落としたくない」 東邦大学医学部(2017) #定積分

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#東邦大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{1} \displaystyle \frac{1-x}{1+x^3} dx$
出典:2017年東邦大学医学部 入試問題
この動画を見る
$\displaystyle \int_{0}^{1} \displaystyle \frac{1-x}{1+x^3} dx$
出典:2017年東邦大学医学部 入試問題
大学入試問題#579「技のかけ方は好みでしょうか」 京都帝国大学(1939) #不定積分

単元:
#大学入試過去問(数学)#積分とその応用#不定積分#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int \displaystyle \frac{\sin^4\ x}{\cos^3\ x} dx$
出典:1939年京都帝国大学 入試問題
この動画を見る
$\displaystyle \int \displaystyle \frac{\sin^4\ x}{\cos^3\ x} dx$
出典:1939年京都帝国大学 入試問題
大学入試問題#578「定数aにかまっていられない」 京都帝国大学(1939) #定積分

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{3a} \displaystyle \frac{2x}{(x^2-a^2)^{\frac{2}{3}}} dx$
出典:1939年京都帝国大学 入試問題
この動画を見る
$\displaystyle \int_{0}^{3a} \displaystyle \frac{2x}{(x^2-a^2)^{\frac{2}{3}}} dx$
出典:1939年京都帝国大学 入試問題
東邦大学医学部医学科(2015) #Shorts #King_property #キングプロパティ

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#東邦大学
指導講師:
ますただ
問題文全文(内容文):
$I=\displaystyle \int_{-2}^{2} \displaystyle \frac{x^22^{-x}}{2^x+2^{-x}} dx$
出典:2015年東邦大学医学部医学科
この動画を見る
$I=\displaystyle \int_{-2}^{2} \displaystyle \frac{x^22^{-x}}{2^x+2^{-x}} dx$
出典:2015年東邦大学医学部医学科
大学入試問題#576「逆に閃かないと苦戦」 京都帝国大学(1938) #不定積分

単元:
#大学入試過去問(数学)#積分とその応用#不定積分#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int \displaystyle \frac{\sin\theta+\cos\theta}{3+\sin2\theta} d\theta$
出典:1938年京都帝国大学 入試問題
この動画を見る
$\displaystyle \int \displaystyle \frac{\sin\theta+\cos\theta}{3+\sin2\theta} d\theta$
出典:1938年京都帝国大学 入試問題
大学入試問題#575「こんな感じかな?で解けるはず」 大阪教育大学(2014) #定積分

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#大阪教育大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{\frac{\pi}{6}} e^{3x}\sin^2\ x\ \sin(x+\displaystyle \frac{\pi}{4})\ dx$
出典:2014年大阪教育大学 入試問題
この動画を見る
$\displaystyle \int_{0}^{\frac{\pi}{6}} e^{3x}\sin^2\ x\ \sin(x+\displaystyle \frac{\pi}{4})\ dx$
出典:2014年大阪教育大学 入試問題
大学入試問題#574「なにかありそう」 東京帝国大学(1938) #不定積分

単元:
#大学入試過去問(数学)#積分とその応用#不定積分#学校別大学入試過去問解説(数学)#東京大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int \displaystyle \frac{1+\sin\ x}{\sin\ x(1+\cos\ x)}\ dx$
出典:1938年東京帝国大学 入試問題
この動画を見る
$\displaystyle \int \displaystyle \frac{1+\sin\ x}{\sin\ x(1+\cos\ x)}\ dx$
出典:1938年東京帝国大学 入試問題
大学入試問題#573「沼にはまらないように!!」 京都帝国大学(1937) #不定積分

単元:
#大学入試過去問(数学)#積分とその応用#不定積分#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int \displaystyle \frac{dx}{x(a^3+x^3)}$
出典:1937年京都帝国大学 入試問題
この動画を見る
$\displaystyle \int \displaystyle \frac{dx}{x(a^3+x^3)}$
出典:1937年京都帝国大学 入試問題
大学入試問題#572「初手どうすべきか」 By 英語orドイツ語さん #不定積分
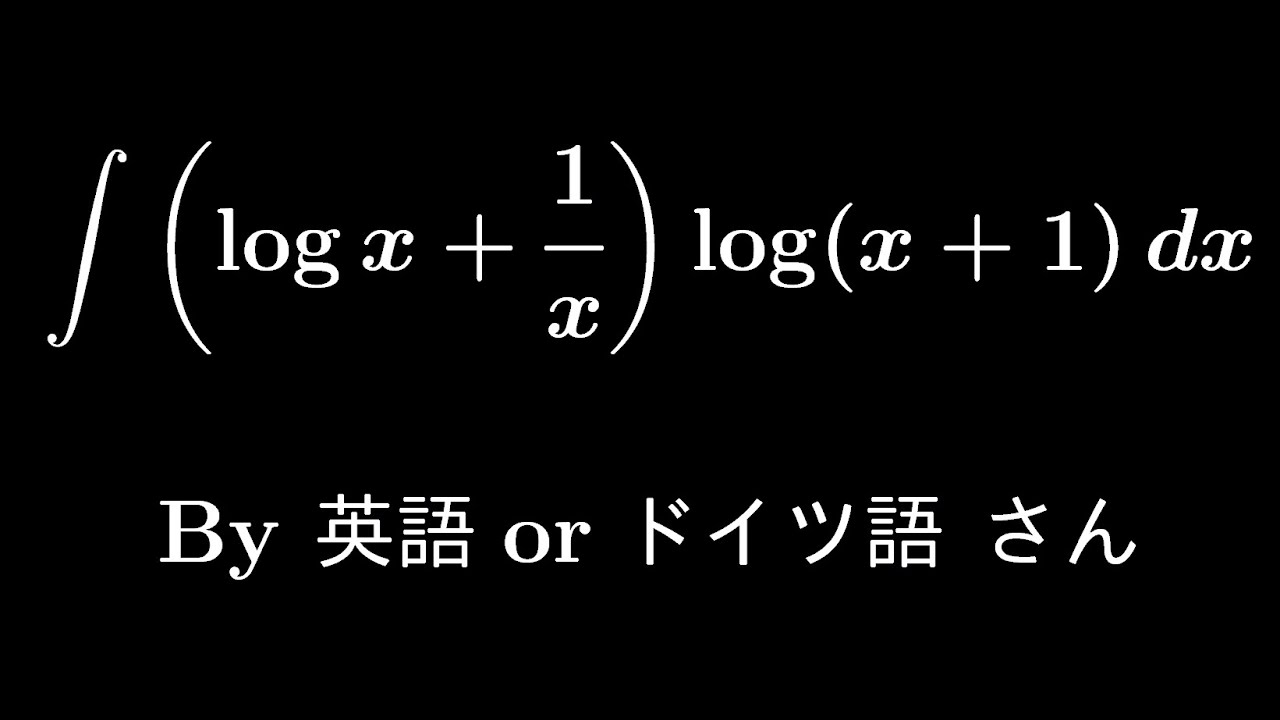
単元:
#積分とその応用#不定積分#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int (log\ x+\displaystyle \frac{1}{x})log(x+1) dx$
この動画を見る
$\displaystyle \int (log\ x+\displaystyle \frac{1}{x})log(x+1) dx$
大学入試問題#570「ほんまにええ問題や~~」 By にっし~Diaryさん #解の個数

単元:
#微分とその応用#関数の変化(グラフ・最大最小・方程式・不等式)#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$x$の方程式
$(x^2-6x+8)^2-k(x^2-6x+8)+4=0$の実数解の個数を調べよ。
この動画を見る
$x$の方程式
$(x^2-6x+8)^2-k(x^2-6x+8)+4=0$の実数解の個数を調べよ。
大学入試問題#569「これは至高の積分」 By Picmin3daisukiさん #不定積分
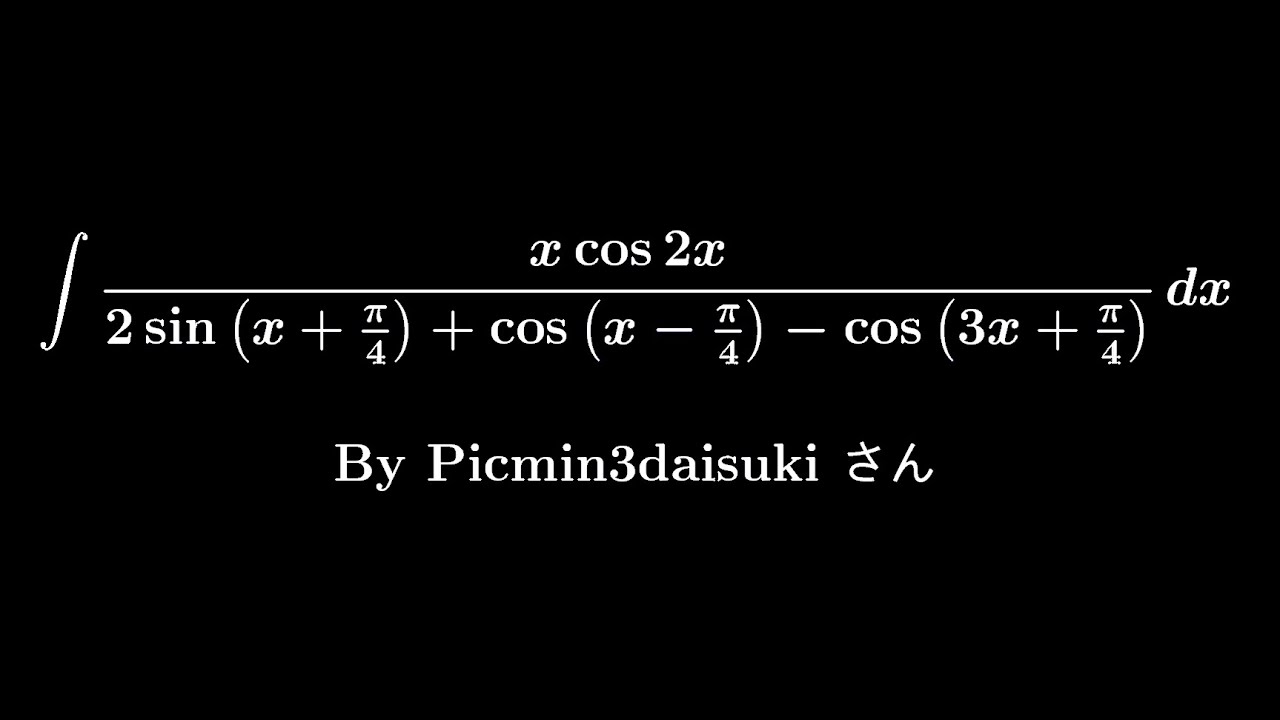
単元:
#積分とその応用#不定積分#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int \displaystyle \frac{x\ \cos\ 2x}{2\sin(x+\displaystyle \frac{\pi}{4})+\cos(x-\displaystyle \frac{\pi}{4})-\cos(3x+\displaystyle \frac{\pi}{4})}\ dx$
この動画を見る
$\displaystyle \int \displaystyle \frac{x\ \cos\ 2x}{2\sin(x+\displaystyle \frac{\pi}{4})+\cos(x-\displaystyle \frac{\pi}{4})-\cos(3x+\displaystyle \frac{\pi}{4})}\ dx$
大学入試問題#568「素直に正面突破」 東京帝国大学(1968) #広義積分

単元:
#大学入試過去問(数学)#関数と極限#積分とその応用#関数の極限#定積分#学校別大学入試過去問解説(数学)#東京大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{ \infty } \displaystyle \frac{xe^{-x}}{(1+e^{-x})^2}\ dx$
出典:1938年東京帝国大学 入試問題
この動画を見る
$\displaystyle \int_{0}^{ \infty } \displaystyle \frac{xe^{-x}}{(1+e^{-x})^2}\ dx$
出典:1938年東京帝国大学 入試問題



